Как нарисовать пересекающиеся плоскости?
Я хочу использовать matplotlib для рисования более или менее фигуры, которую я прикрепил ниже, которая включает в себя две пересекающиеся плоскости с нужной степенью прозрачности, указывающей их относительную ориентацию, а также круги и векторы в двух плоскостях, спроецированных в 2D.
Я не уверен, есть ли существующий пакет для этого, какие-либо подсказки?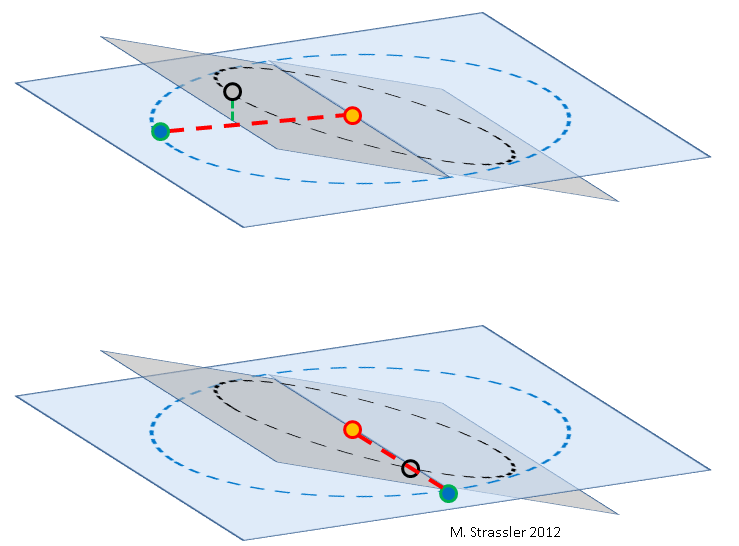
2 ответа
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
dim = 10
X, Y = np.meshgrid([-dim, dim], [-dim, dim])
Z = np.zeros((2, 2))
angle = .5
X2, Y2 = np.meshgrid([-dim, dim], [0, dim])
Z2 = Y2 * angle
X3, Y3 = np.meshgrid([-dim, dim], [-dim, 0])
Z3 = Y3 * angle
r = 7
M = 1000
th = np.linspace(0, 2 * np.pi, M)
x, y, z = r * np.cos(th), r * np.sin(th), angle * r * np.sin(th)
ax.plot_surface(X2, Y3, Z3, color='blue', alpha=.5, linewidth=0, zorder=-1)
ax.plot(x[y < 0], y[y < 0], z[y < 0], lw=5, linestyle='--', color='green',
zorder=0)
ax.plot_surface(X, Y, Z, color='red', alpha=.5, linewidth=0, zorder=1)
ax.plot(r * np.sin(th), r * np.cos(th), np.zeros(M), lw=5, linestyle='--',
color='k', zorder=2)
ax.plot_surface(X2, Y2, Z2, color='blue', alpha=.5, linewidth=0, zorder=3)
ax.plot(x[y > 0], y[y > 0], z[y > 0], lw=5, linestyle='--', color='green',
zorder=4)
plt.axis('off')
plt.show()
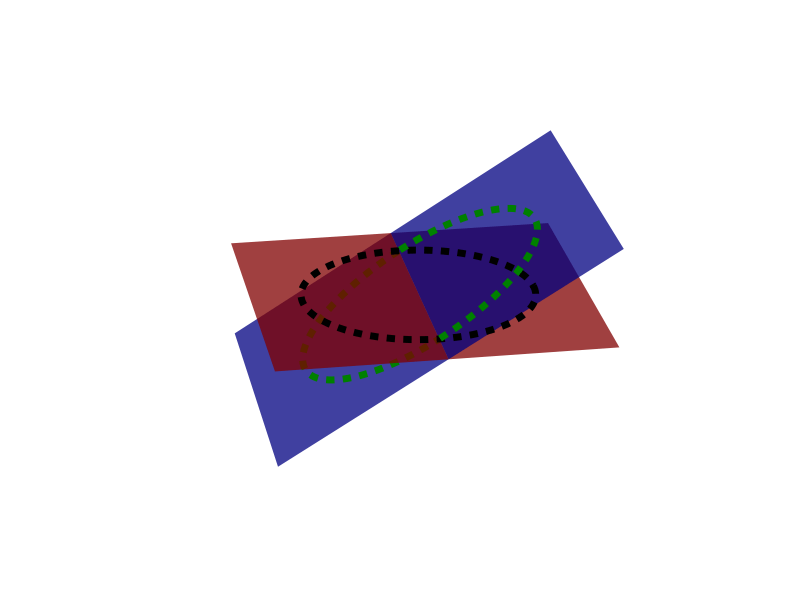
предостережения:
Я использую версию, очень близкую к текущему мастеру, поэтому я не уверен, что будет работать в старых версиях
Причиной разделения графика является то, что "выше" и "ниже" определяются каким-то непонятным образом (я не совсем уверен, что
zorderна самом деле ничего не делает), и действительно зависит от порядка, в котором нарисованы художники. Таким образом, поверхности не могут пересекаться (одна будет находиться над другой везде), поэтому вам необходимо наносить участки по обе стороны пересечения отдельно. (Вы можете видеть это по черной линии, на которой я не разбил, похоже, что это "сверху" верхней синей плоскости)."Правильное" упорядочение поверхностей также зависит от угла обзора.
Matplotlib имеет возможность трехмерного проецирования, но пунктирные линии рисуются с постоянной шириной на конечном 2D-изображении, а не выглядят так, как если бы они лежали плоско на наклонных плоскостях. Если геометрия простая и круговая "орбита", это может сработать, но если вы хотите нарисовать эллипсы, видимые под углом, зрителю может потребоваться больше визуальных подсказок для всей трехмерной схемы.
Если бы мне нужно было сделать одну красивую причудливую иллюстрацию, подобную этой, но еще более красивую и причудливую, и ее не нужно было автоматизировать, я бы начал с создания графики - по крайней мере, пунктирной линии - для каждой плоскости, как простое плоское 2D-изображение, использующее то, что кажется удобным в данный момент - программу для векторного рисования, такую как Illustrator или Inkscape, или в matplotlib, если есть данные, которым нужно следовать.
Затем я бы использовал POV-Ray или Blender для моделирования самолетов под любым углом, сферы для круглых вещей (планет?). Уже созданная 2D-графика станет текстурой, которая будет отображаться на плоскости. POV-Ray использует язык сценариев, позволяющий хранить, изменять и копировать записи для будущих проектов. Если это действительно один раз, и я не возражаю делать все вручную, Блендер хорош. Какой бы инструмент я ни использовал, в результате получается изображение, показывающее желаемую проекцию трехмерных геометрических элементов в 2D.
Являются ли круглые вещи, которые я называю "планетами", должны быть плоскими кругами в финальной работе, как в примерах? Затем я бы нарисовал их с помощью приложения для векторного рисования поверх визуализированного 3D-изображения. Но я подозреваю, что вы предпочли бы сферы в 3D.
Показанные образцы не имеют освещения или теней. Тени помогут прояснить геометрию в 3D, хотя первая из этих двух иллюстраций не так уж и плоха. Короткая зеленая линия, показывающая планету наклонной плоскости над красной линией, кажется достаточно четкой, но тень поможет. Вторая иллюстрация выглядит немного более запутанной в отношении формы, расположения пересечений различных объектов. Здесь тени помогут больше. POV-Ray или Blender с радостью создадут их без особых усилий. Более того, взаимные отражения, известные как излучение, помогают видеть трехмерные отношения на двухмерных изображениях. Этот продвинутый эффект легко сделать в наши дни, не требуя опыта в оптике или графике, просто зная, что он существует.
Конечно, этот совет бесполезен, если вы уже не знакомы с 3D-графикой и такими инструментами, как POV-Ray.
Для автоматизированного решения лучше всего использовать OpenGL в некоторых быстрых и грязных программах. Тени могут потребовать некоторой работы, все же.