Как решить ближайшего соседа через R-ближайший сосед?

Question

Ссылаясь на руководство по E2LSH (не важно, что об этой конкретной библиотеке, эта цитата должна быть верной для проблемы NN в целом):

E 2LSH может также использоваться для решения проблемы ближайшего соседа, где, учитывая запрос q, структура данных требует отчета о точке в P, ближайшей к q. Это можно сделать, создав несколько структур данных R-ближнего соседа, для R = R1, R2, .,, Rt, где Rt должно быть больше максимального расстояния от любой точки запроса до ближайшего соседа. Затем ближайший сосед может быть восстановлен путем запроса структур данных в возрастающем порядке радиусов, останавливаясь всякий раз, когда найдена первая точка

Может кто-нибудь перефразировать это, пожалуйста? Я не делаю эту процедуру, чтобы найти ближайшего соседа, используя подход R-ближнего соседа.

Answer 1

Я приведу пример, который должен прояснить ситуацию. Предположим, что наш набор данных состоит только из одной точки, p и точка запроса прибывает, q, Давайте предположим, ^* что расстояние p а также q 3,9.

Теперь, используя E2LSH ^$, я могу создать структуру данных, которая решает проблему R-ближайшего соседа, то есть она ответит да (и выберет мне точку), которая находится внутри радиуса R. Если такой точки не существует, она ответит нет.

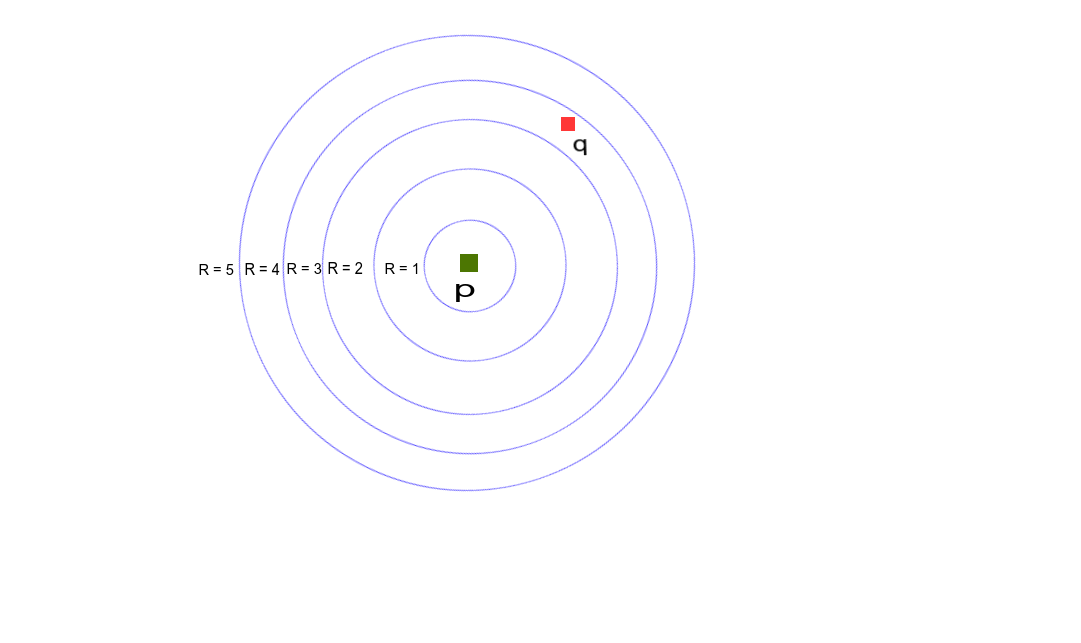
Допустим, я решил построить 5 структур данных такого рода, начиная с R = 1 до 5. На наш взгляд, это то, что мы сделали до сих пор:

Итак, теперь помните, что d(p, q) = 3,9, поэтому мы ожидаем спросить структуру данных, которая построена с R = 4, и найти для нас точку запроса q,

Теперь давайте притворимся, что мы не знаем d(p, q), поэтому мы начинаем поиск с наименьшего радиуса, который мы выбрали, то есть 1. Итак, мы спрашиваем, есть ли что-нибудь в радиусе (равное 1) из нашего набора данных? Нет!

От R = 2? Нет! С R = 3? Нет! С R = 4? Да и это q! Итак, мы закончили. 4 - это то, что вы упоминаете в своем вопросе.

---

* _{Это сильное предположение, и E2LSH страдает от необходимости вводить пользователя для ввода этого параметра R, поскольку обычно мы не знаем, какое значение должно иметь R, слишком большое, и мы будем тратить пространство и время, слишком малое, и не найдем наш запрос!}

$ _{Я слышал, что на домашней странице Ильи Разенштейна есть что-то более современное, чем E2LSH.}