В поисках дополнения DFA?
Меня просят показать диаграмму DFA и RegEx для дополнения RegEx (00 + 1)*, В предыдущей задаче мне пришлось доказать, что дополнение DFA является замкнутым и также является регулярным выражением, поэтому я знаю, что для преобразования DFA, M в дополнение, M`, мне просто нужно поменять начальные состояния принятия и окончательно принимающие государства.
Тем не менее, похоже, что начальные принимающие состояния для RegEx {00, 1, ^} и окончательные принимающие состояния {00, 1, ^} также. Так что их замена приведет только к тому же RegEx и DFA, что кажется противоречивым.
Я делаю что-то не так или у этого RegEx не должно быть реального дополнения?
Спасибо
2 ответа
Как вы говорите в вопросе:
Я знаю, что для преобразования DFA, M в дополнение к M, мне просто нужно поменять начальные принимающие состояния и конечные принимающие состояния.
Это не дополнение, но вы делаете что-то вроде обращения к языку, а обычные языки закрываются при обращении.
Обращение DFA
Что такое язык разворота?
Обращение языка L (обозначается L R) - это язык, состоящий из обращения всех строк в L.
Учитывая, что L есть L(A) для некоторой FA A, мы можем построить автомат для L R:
перевернуть все ребра (дуги) в диаграмме переходов
принимающее состояние для автомата L R является начальным состоянием для A
создать новое начальное состояние для нового автомата с эпсилон-переходами в каждое из принимаемых состояний для A
Примечание. Если поменять местами все стрелки и поменять местами начальные и принимающие состояния DFA, вместо этого вы можете получить NFA.
вот почему я написал FA(не DFA)
Дополнение DFA
В поисках дополнения DFA?
Defination: Дополнение языка определяется с точки зрения разности множеств от Σ* (сигма-звезда). то есть L ' = Σ * - L.
И язык дополнения (L ') в L имеет все строки из Σ* (сигма-звезда), за исключением строк в L. Σ* - все возможные строки над алфавитом Σ.
Σ = набор языковых символов
Чтобы построить DFA D, который принимает дополнение к L, просто преобразуйте каждое принимающее состояние в A в неприемлемое состояние в D и преобразуйте каждое непринятое состояние в A в принимающее состояние в D.
(Внимание! Это не относится к NFA)
A является DFA L, D для дополнения
Примечание. Чтобы создать дополнительный DFA, старый DFA должен быть полным средством, позволяющим получить все возможные преимущества от каждого состояния (или, другими словами, δ должна быть полная функция).
Дополнение DFA для регулярного выражения
(00+1)*
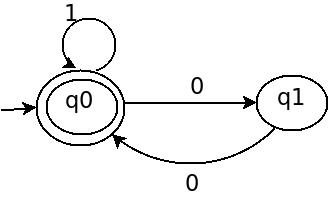
ниже DFA с именем A:
Но не этот DFA не полный DFA. функция перехода δ частично определено, но не для полного домена Q×Σ (пропуская идущий край от q1 для лейбла 1).
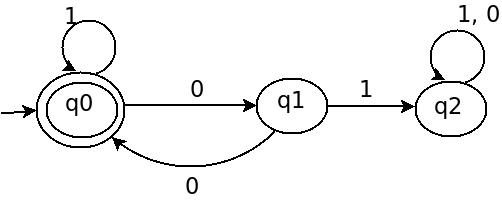
Его полное DFA может быть следующим (A):
В указанном выше DFA определены все возможные транзакции (* для каждой пары Q,Σ *) а также δ это полная функция в этом случае.
Рефф: узнать, что такое частичная функция.
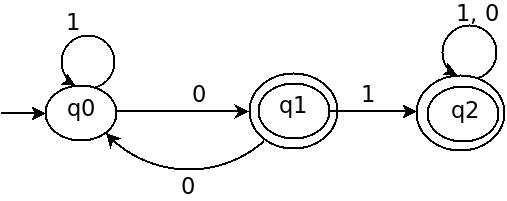
Новое дополнение DFA D может быть построено путем изменения всех конечных состояний q0 не конечные состояния и наоборот.
Так в дополнение q0 стать не финальным и q1, q2 являются окончательными состояниями.
Теперь вы можете написать Регулярное выражение для языка дополнения, используя теорию ARDEN'S THEOREM и DFA, которые я дал.
Здесь я пишу регулярное выражение для дополнения напрямую:
(00 + 1)*0(^ + 1(1 + 0)*)
где ^ является нулевым символом
некоторые полезные ссылки:
Отсюда и через мой профиль вы можете найти более полезные ответы на FA. Кроме того, две хорошие ссылки на свойства обычного языка: один, второй
Я не нашел времени, чтобы прочитать весь ответ Грижеша, но вот простой способ получить DFA, принимающий дополнение языка, с учетом DFA, принимающего язык: используйте тот же DFA, но измените принимающие состояния на непринятые, и наоборот.
Ранее принятые строки будут отклонены, а ранее отклоненные строки будут приняты. Поскольку все переходы должны быть определены в любом допустимом DFA, и поскольку все входные строки приводят к ровно одному состоянию, это всегда работает.
Чтобы получить DFA для аннулирования, вы можете сначала создать NFA, добавив новое начальное состояние, которое недетерминировано разветвляется на все принимающие состояния исходного DFA. Отмените все переходы исходного DFA и сделайте единственное принимающее состояние начальным состоянием исходного DFA.