Какие рекурсивные функции нельзя переписать с помощью циклов?
Насколько я знаю, большинство рекурсивных функций можно переписать с помощью циклов. Некоторые могут быть сложнее, чем другие, но большинство из них можно переписать.
При каких условиях становится невозможным переписать рекурсивную функцию с помощью цикла (если такие условия существуют)?
10 ответов
Когда вы используете функцию рекурсивно, компилятор позаботится об управлении стеками, что делает рекурсию возможной. Все, что вы можете сделать рекурсивно, вы можете сделать, управляя стеком самостоятельно (для косвенной рекурсии вам просто нужно убедиться, что ваши различные функции совместно используют этот стек).
Итак, нет, ничего нельзя сделать с помощью рекурсии и нельзя сделать с помощью цикла и стека.
Любая рекурсивная функция может быть сделана для итерации (в цикл), но вам нужно использовать стек самостоятельно, чтобы сохранить состояние.
Обычно хвостовую рекурсию легко преобразовать в цикл:
A(x) {
if x<0 return 0;
return something(x) + A(x-1)
}
Можно перевести на:
A(x) {
temp = 0;
for i in 0..x {
temp = temp + something(i);
}
return temp;
}
Другие виды рекурсии, которые можно перевести в хвостовую рекурсию, также легко изменить. Другие требуют больше работы.
Следующие:
treeSum(tree) {
if tree=nil then 0
else tree.value + treeSum(tree.left) + treeSum(tree.right);
}
Это не так просто перевести. Вы можете удалить одну часть рекурсии, но другую невозможно без структуры для хранения состояния.
treeSum(tree) {
walk = tree;
temp = 0;
while walk != nil {
temp = temp + walk.value + treeSum(walk.right);
walk = walk.left;
}
}
Каждая рекурсивная функция может быть реализована с помощью одного цикла.
Просто подумайте, что делает процессор, он выполняет инструкции в одном цикле.
Я не знаю примеров, когда рекурсивные функции не могут быть преобразованы в итеративную версию, но непрактичными или крайне неэффективными примерами являются:
обход дерева
быстрый фурье
быстрые сортировки (и некоторые другие iirc)
По сути, все, что вам нужно, чтобы начать отслеживать безграничные потенциальные состояния.
Дело не в том, что они не могут быть реализованы с использованием циклов, а в том, что способ, которым работает рекурсивный алгоритм, намного яснее и более кратким (и во многих случаях математически доказуемым), что функция корректна.
Многие рекурсивные функции могут быть написаны как рекурсивные в хвостовом цикле, которые могут быть оптимизированы для цикла, но это зависит как от алгоритма, так и от используемого языка.
Все они могут быть записаны как итеративный цикл (но некоторым все еще может понадобиться стек, чтобы сохранить предыдущее состояние для последующих итераций).
Одним из примеров, который было бы чрезвычайно трудно преобразовать из рекурсивного в итеративный, была бы функция Аккермана.
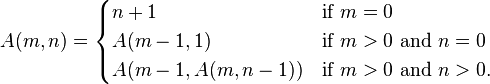
В SICP авторы бросают вызов читателю, чтобы он придумал чисто итеративный метод реализации проблемы "подсчета изменений" ( вот пример из Project Euler).
Но строгий ответ на ваш вопрос уже был дан - циклы и стеки могут реализовать любую рекурсию.
Косвенную рекурсию все еще можно преобразовать в нерекурсивный цикл; просто начните с одной из функций и выполняйте вызовы других до тех пор, пока не получите непосредственно рекурсивную функцию, которую затем можно преобразовать в цикл, использующий структуру стека.
Вы всегда можете использовать цикл, но вам может потребоваться создать больше структуры данных (например, имитировать стек).