Почему заполнение нулями в области Фурье приводит к сложному обратному преобразованию?

Question

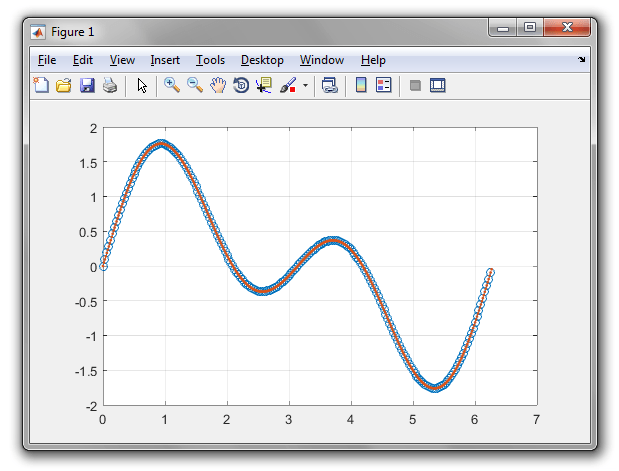
Если я начну с сигнала, который имеет только реальные значения, выполнение fft и ifft возвращает точный сигнал без сложных записей, как ожидалось. Но если я заполняю fft нулями, чтобы получить интерполированные значения во временной области, обратное fft всегда оказывается сложным двойным числом. Я позаботился о том, чтобы выполнить fftshift() и затем заполнить обе стороны, чтобы не нарушить симметрию. Ниже приведен пример кода, который показывает это поведение. Я смотрю на это неправильно или вычислительная ошибка после заполнения нуля слишком велика? Как мне преодолеть это?

Код:

%%%%%%%%%

x=linspace(0,2*pi,200);

y = sin(x)+sin(2*x);

Y = fftshift(fft(y));

n=400;

x1 = linspace(0,2*pi,n);

Y1 = zeros(1,n);

Y1((n-200)/2+1:end-(n-200)/2) = Y;

y2 = ifft(fftshift(2*Y1));

plot(x,y);

hold on;

plot(x1,y2(1:end),'x-');

isreal(y)==isreal(y2)

%%

Answer 1

Вероятно, отключение на одну ошибку или игнорирование микроскопических значений ошибки округления. Чтобы результат IFFT был строго реальным (за исключением крошечных числовых величин шума), комплексный входной вектор должен быть точно сопряженным симметричным вокруг элемента 0 (или около N/2 для четного N).

Answer 2

Есть несколько небольших проблем с вашим кодом:

1. Количество выборок исходного сигнала и его БПФ должно быть нечетным. Чтобы понять почему, обратите внимание, что первая запись FFT - это компонент с нулевой частотой, который не имеет симметричной частоты. Количество оставшихся частот должно быть четным, чтобы их можно было разделить на две симметричные части, а дополнительные нули можно вставить между двумя частями.

2. Оси времени не должны создаваться с linspace, поскольку linspace исправляет обе конечные точки, вы не получите точный масштабный коэффициент 2, Для этого вам нужно создать оси вручную с помощью : (colon).

3. Второй fftshift должно быть ifftshift, Это не важно здесь, потому что БПФ с нулевой подкладкой имеет четный размер и так fftshift а также ifftshift совпадают. Но, как правило, вы должны использовать ifftshift отменить действие fftshift,

Итак, код становится:

x = (0:200)/201*2*pi;
y = sin(x)+sin(2*x);
Y = fftshift(fft(y));
x1 = (0:401)/402*2*pi;
Y1 = [zeros(1,101) Y zeros(1,100)];
y2 = ifft(ifftshift(2*Y1)); % or fftshift, since length is even
plot(x,y,'o-');
hold on;
plot(x1,y2,'.:');
isreal(y)==isreal(y2)
max(abs(y-y2(1:2:end))) % should be of the order of eps

Теперь мы можем проверить это

• Оба сигнала реальны:

  >> isreal(y)==isreal(y2)
  ans =
    logical
     1
  

  Лучшим тестом было бы проверить, что мнимая составляющая y1 (который может быть не совсем нулевым из-за проблем с числовой точностью) имеет порядок eps,

• Каждый второй образец y1 совпадает с соответствующим образцом в y, с точностью до числовых ошибок порядка eps:

  >> max(abs(y-y2(1:2:end)))
  ans =
       6.661338147750939e-16