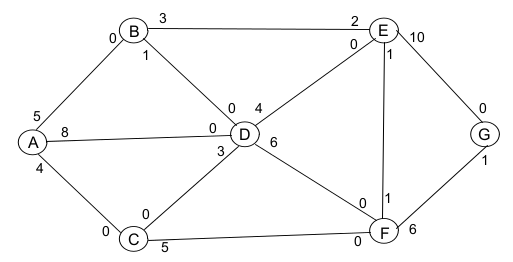
Неровность Форда-Фулкерсона (множественные вершины против обратного потока)
До сих пор я работал с графами, вершины которых имеют только одно направленное ребро между ними. Для всех примеров, которые я использовал для проверки своей реализации, был получен правильный ответ. Однако, когда я использую график, содержащий вершины, ребро которых движется в обоих направлениях, я не даю правильного ответа. Я рассматривал такой край, идущий назад, как обратный поток между этими двумя вершинами, так как кажется, что обратный поток и другая "труба", идущая назад, в конечном итоге будут эквивалентны. Мое предположение здесь неверно?
1 ответ
Предположение, что два ребра с емкостью "а" и "б" U--[a]-->V а также V--[b]-->U эквивалентно одному ребру U--[a-b]-->V это неверно. Предполагая, что a> b, отрицательный поток до -b допустим в первом случае, но недопустим во втором случае.
Вы можете суммировать только пропускную способность ребер в одном направлении. На приведенном ниже графике добавление двух противоположных трубок от E до F и от F до E делает их исчезающими из графика, изменяя оптимальное решение.