Проблема различия между gimp bicubic и стандартным bicubic

Question

Я сделал бикубическую интерполяцию, которая ссылается здесь. Но я обнаружил довольно небольшую разницу между результатами GIMP и моего собственного кода. Это оригинальное изображение

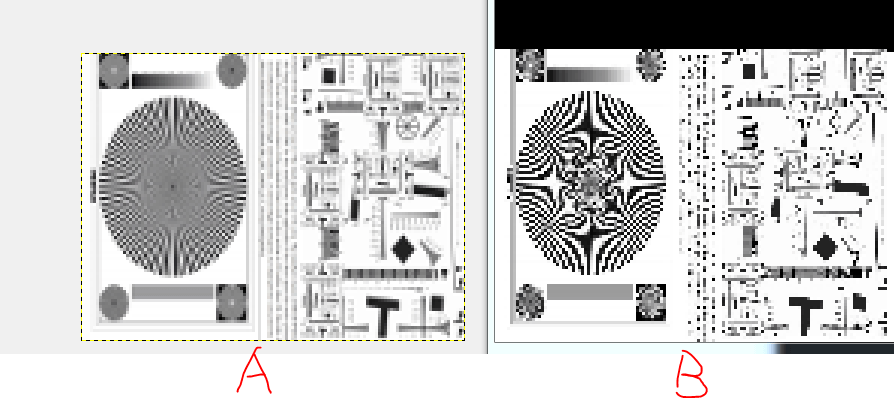
Как вы можете видеть выше 2 изображения (A) это Gimp's (B) мой собственный код со ссылкой.

Я запутался, что сделал что-то не так? Должен ли я изменить алгоритм?

Не могли бы вы дать совет?

Answer 1

Вы понижаете, а не повышаете. Сама интерполяция отлично работает при повышении частоты дискретизации (увеличение количества пикселей).

При понижающей дискретизации, либо с нашей без интерполяции, вы выбрасываете информацию и получаете псевдонимы. Это эффект, который вы видите в своем результате.

Gimp при понижающей дискретизации сначала сглаживает изображение. Сглаживание удаляет более высокие частоты, которые в противном случае были бы наложены.

Чтобы получить результаты, аналогичные Gimp, примените фильтр нижних частот перед понижением частоты дискретизации.

---

Вот пример понижающей дискретизации с и без фильтрации нижних частот. Я использую MATLAB с DIPimage, потому что это легко для меня, а вы не указали язык программирования. В любом случае, это просто для иллюстрации принципа.

У меня прямая выборка с целочисленным множителем, у вас уже есть код, чтобы сделать то же самое с нецелым множителем, я не хочу, чтобы это отвлекало.

s1 просто понижающая дискретизация, без сглаживания. Похоже, ваш результат. Это псевдоним.

s2 а также s3 использовать гауссовские фильтры нижних частот разных размеров. Я использовал сигмы 8*0.5 а также 8*0.8 Вот. После понижающей выборки они соответствуют сигмам 0,5 и 0,8 соответственно. Первый немного маловат, он все же демонстрирует некоторый псевдоним, но намного меньше. Это также все еще острый. Второй - правильный размер для предотвращения алиасинга (менее 1% энергии или около того - алиас).

s4 использует идеальную фильтрацию нижних частот (в области Фурье). Я не рекомендую этот метод, потому что он вызывает много звонков. Это просто здесь для сравнения. В выходных данных присутствует псевдоним 0%, и результат настолько резкий, насколько это возможно при этом размере.

a = readim('https://stackru.com/images/569c675d543e3745d1126c2dc8a14b81e27836cd.jpg');
a = a{1};

f = 8; % subsample by a factor 8

s1 = a(0:f:end,0:f:end);

s2 = gaussf(a,f*0.5);
s2 = s2(0:f:end,0:f:end);

s3 = gaussf(a,f*0.8);
s3 = s3(0:f:end,0:f:end);

s4 = ft(a);
s4 = cut(s4,imsize(s1));
s4 = real(ift(s4) / numel(a) * numel(s4));