Алгоритм нахождения биекции между массивами

Question

У меня есть два массива, скажем A={1, 2, 3} а также B={2, 4, 8} (Количество элементов массива и номера могут отличаться). Как мне найти биекцию между массивами.

В этом случае это было бы f:A->B; f(x)=2^(x)

Answer 1

Как отметили другие, эта проблема плохо определена.

Другими возможными функциями, которые дают такие же результаты, являются (среди, вероятно, бесконечные другие): (8 x)/3 - x^2 + x^3/3, x + (37 x^2)/18 - (4 x^3)/3 + (5 х ^4)/18 и (259 х ^3)/54 - (31 х ^4)/9 + (35 х ^5)/54.

Я нашел эти решения, используя:

n = 5; (* try various other values *)
A = {1, 2, 3} ; B = {2, 4, 8}
eqs = Table[
  Sum[a[i] x[[1]]^i, {i, n}] == x[[2]], {x, {A, B}\[Transpose]}]
sol = Solve[eqs, Table[a[i], {i, n}], Reals]
Sum[a[i] x^i, {i, n}] /. sol

Иногда не все a[i] полностью определены, и вы можете придумать свои собственные ценности.

[совет: лучше не использовать переменные, начинающиеся с заглавной буквы в Mathematica, чтобы не вступать в конфликт с зарезервированными словами]

Answer 2

Я не думаю, что эта проблема имеет общее решение. Вы можете попробовать FindSequenceFunction, но она не всегда найдет решение. Для рассматриваемого случая вам понадобятся более длинные списки:

In[250]:= FindSequenceFunction[Transpose[{{1, 2, 3}, {2, 4, 8}}], n]

Out[250]= FindSequenceFunction[{{1, 2}, {2, 4}, {3, 8}}, n]

но

In[251]:= FindSequenceFunction[Transpose[{{1, 2, 3, 4}, {2, 4, 8, 16}}], n]

Out[251]= 2^n

Вы также можете играть с FindFitЕсли у вас есть предположения о биекции:

In[252]:= FindFit[Transpose[{{1, 2, 3}, {2, 4, 8}}], p*q^x, {p, q}, x]

Out[252]= {p -> 1., q -> 2.}

Answer 3

Поскольку вы помечаете Mathematica, я буду использовать функции Mathematica в качестве ссылки.

Если вас интересует произвольное согласование ваших данных с гладкой функцией, вы можете использовать интерполяцию. Например

a = {1, 2, 3}; b = {2, 4, 8};
f = Interpolation[Transpose[{a, b}]];

(* Graph the interpolation function *)
Show[Plot[f[x], {x, 1, 3}], Graphics[Point /@ Transpose[{a, b}]], 
   PlotRange -> {{0, 4}, {0, 9}}, Frame -> Automatic, Axes -> None]

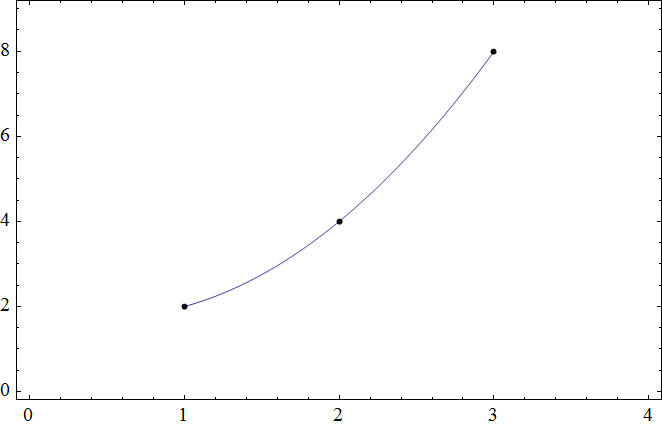
Интерполяция использует кусочные полиномы. Вы можете сделать то же самое на своем любимом языке программирования, если вы знаете или хотите немного узнать о численных методах, особенно B-сплайнах.

Если вместо этого вы что-то знаете о своих данных, например, что они имеют форму c d^x, то вы можете сделать минимизацию, чтобы найти неизвестные (в данном случае c и d). Если ваши данные на самом деле сгенерированы из формы c d^x, то подгонка будет справедливой, в противном случае ошибка минимизируется в смысле наименьших квадратов. Итак, для ваших данных:

FindFit[Transpose[{a, b}], c d^x, {c, d}, {x}]

доклады:

{c -> 1., d -> 2.}

Указывает, что ваша функция 2^x, так же, как вы знали все это время.