Непонятно, как понимать нотацию
У меня проблемы с этой одной проблемой
9n <= cn^3
в основном я могу приступить к
9/c <= n^2
Но как мне решить остальное?
3 ответа
Значение little o является
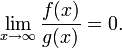 мы говорим
мы говорим f(x)=o(g(x)),
пусть f(x)=9*x и g(x)=c*x^3, где c - положительная постоянная. когда x стремится к бесконечности, f(x)/g(x) стремится к 0. поэтому мы можем сказать, f(x)=o(g(x)),
асимптотические обозначения применимы для достаточно большого значения n.so для большого значения n
9n << cn^3
для всех с>0.
Прочитайте эту ссылку, чтобы получить ссылку ниже-вниз big-O и little-O
см. в случае вашего уравнения, когда n=3, оно становится 9*3=23=3^3, поэтому для n<3 9n > n^3. так что если вы выберете c в качестве любого числа, чтобы 9n<=n^3 при n <3, тогда оно может быть в O(n).
Вам просто нужно показать это для каждого c E сть n0 такой что для всех n > n0: 9n <= n^3, Просто решив это уравнение n вы получаете (при условии n положительный):
n >= 3/sqrt(c)
Теперь возьми n0 = 3/sqrt(c), которая существует и является позитивной для всех c > 0тогда для всех n > n_0 с обратным расчетом:
cn^3-9n = n*(cn^2-9)
= n*c*(n^2-9/c)
= n*c*(n-3/sqrt(c))*(n+3/sqrt(c))
= n*c*(n-n0)*(n+n0)
> 0
(так как n>n0>0, c>0, n>n0 а также n>n0>-n0)
и поэтому
9n < cn^3
Который означает, что 9n in o(n^3),