Фильтр Хэмминга в частотно-пространственной области

Question

Я хочу удалить артефакт Гиббса в одномерном сигнале, применив фильтр Хемминга к нему в MATLAB.

Что у меня есть k1 который является сигналом в частотной области. Я могу получить сигнал во временной области, применяя DFT на k1:

s1 = ifft(ifftshift(k1));

Этот сигнал имеет артефакт Гиббса. Теперь я хочу удалить его путем (A) умножения фильтра Хемминга на k1 в частотной области и (B) свертки IFFT фильтра Хемминга с s1 в пространственной области. Я ожидаю одинаковый результат от обоих из них:

% (A) Multiplying Hamming filter to `k1`
n = size(k1,2);
wk = hamming(n,'symmetric')'; 
k2 = wk.*k1;
s2 = ifft(ifftshift(k2));

% (B) Convolving IFFT of Hamming filter with `s1`
wx = ifft(ifftshift(wk));
s3 = conv(s1,wx,'same');

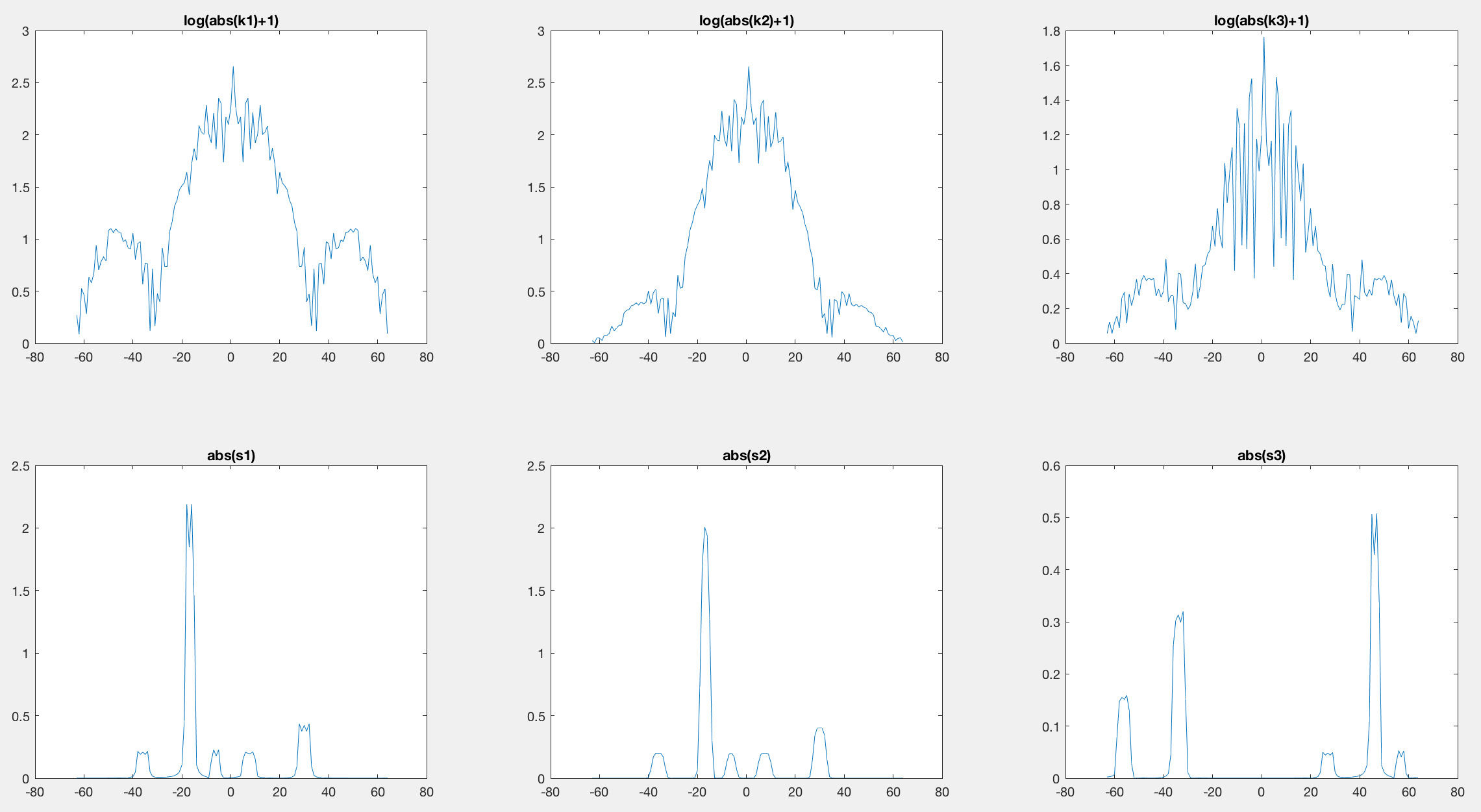
Результат (А), s2, кажется правильным, поскольку сигнал выглядит размытым, а артефакт Гиббса исчез. Тем не менее, результат (B), s3, совершенно другой и неверный. Чего не хватает в (B)? (Пожалуйста, скачайте k1.mat по этой ссылке, если вам это нужно.)

Answer 1

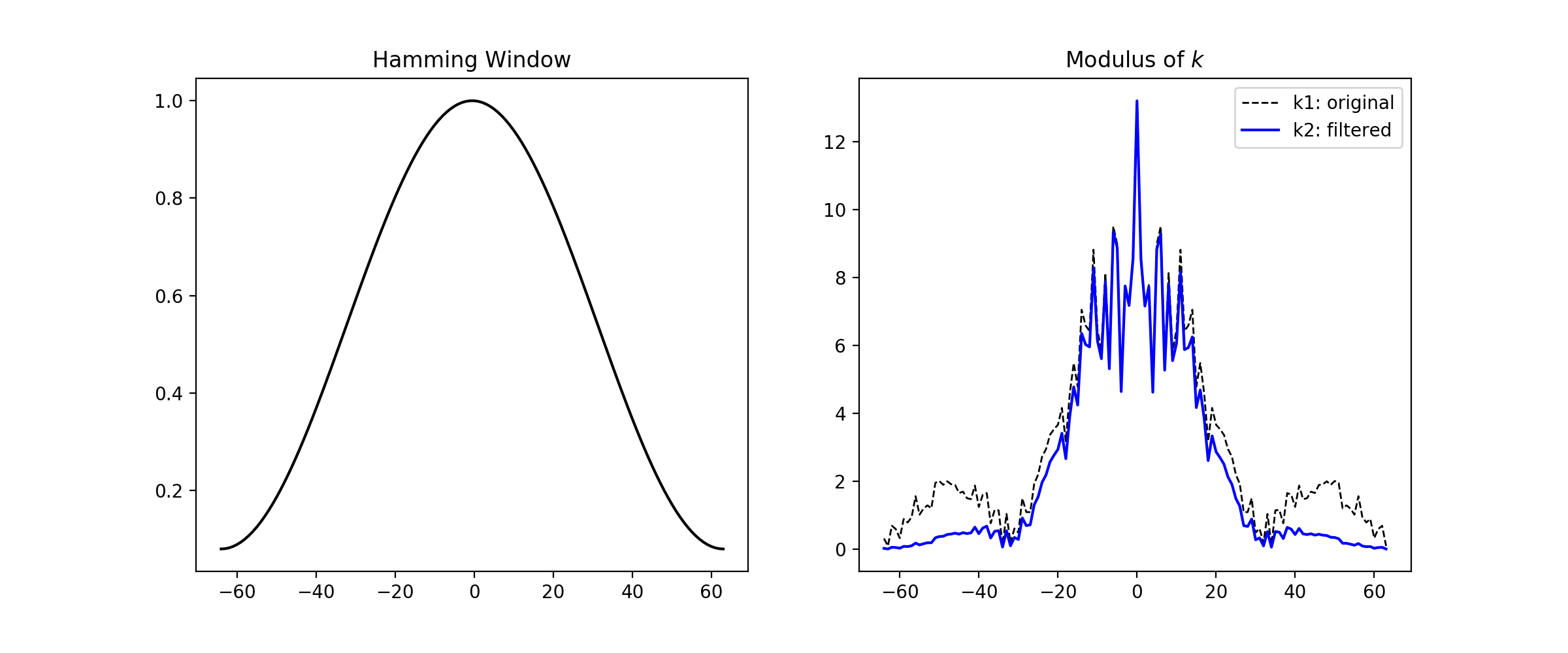
Из данных вы разместили то, что вы называете "Гиббс" на space высокочастотные компоненты по частоте. Когда вы умножаете свое окно Хэмминга на частоту, вы сглаживаете эти более высокие частоты. Они находятся в границах (отрицательных и положительных) вашего сложного массива k1.

Сильфон это то, что происходит, когда вы делаете k2 = wk.*k1;

Вот почему ваш так называемый космический "Гиббс" исчез.

Это не странное использование окна Хэмминга, которое обычно применяется на time|space уменьшить частоту Гиббса при отсечении и дискретизации сигнала, функции или ядра фильтра на time|space,

Чтобы воспроизвести это в space вам нужно было бы разработать очень плавный фильтр низких частот, который будет давать частотный отклик окна Хэмминга для создания этой свертки. Я не помню обратного преобразования окна Хэмминга, но вы могли бы использовать фильтр Гаусса.

Btw wx = ifft(ifftshift(wk)); дает wx не симметричен относительно своего максимума.