Получить производную ECDF

Question

Можно ли дифференцировать ECDF? Возьмите пример, полученный в следующем примере.

set.seed(1)

a <- sort(rnorm(100))
b <- ecdf(a)

plot(b)

Я хотел бы взять производную b чтобы получить его функцию плотности вероятности (PDF).

Answer 1

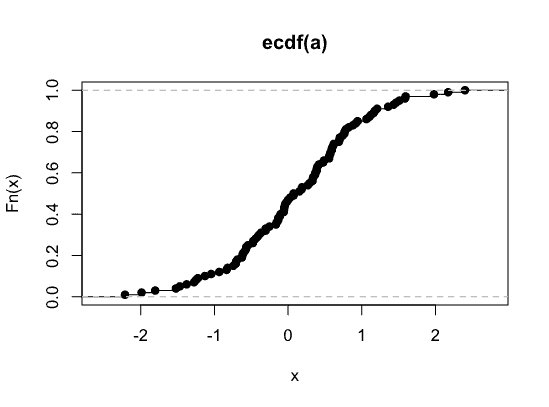
n <- length(a)  ## `a` must be sorted in non-decreasing order already
plot(a, 1:n / n, type = "s")  ## "staircase" plot; not "line" plot

Однако я ищу, чтобы найти производную b

В статистике на основе выборок расчетная плотность (для непрерывной случайной величины) не получается из ECDF путем дифференцирования, поскольку размер выборки конечен и ECDF не дифференцируем. Вместо этого мы оцениваем плотность напрямую. Похоже plot(density(a)) это то, что вы действительно ищете.

---

несколько дней спустя..

Внимание: ниже приведено только численное решение без статистического обоснования!

Я принимаю это как упражнение, чтобы узнать о пакете R scam для аддитивных моделей с ограниченными формами, дочерний пакет mgcv раннего аспиранта профессора Вуда доктора Пя.

Логика такова:

• с помощью scam::scam установите монотонно увеличивающийся P-сплайн в ECDF (вы должны указать, сколько узлов вы хотите); [Обратите внимание, что монотонность не единственное теоретическое ограничение. Требуется, чтобы сглаженный ECDF "обрезался" по двум его краям: левому краю в 0 и правому краю в 1. В настоящее время я использую weights наложить такое ограничение, придав очень большой вес двум краям]
• с помощью stats::splinefun репараметризовать подогнанный сплайн с помощью монотонного интерполяционного сплайна через узлы и прогнозируемые значения в узлах;
• возвратите сплайн-функцию интерполяции, которая также может вычислять 1-ю, 2-ю и 3-ю производные.

Почему я ожидаю, что это сработает:

Как размер выборки растет,

• ECDF сходится к CDF;
• P-сплайн является последовательным, поэтому сглаженный ECDF будет все более беспристрастным для ECDF;
• 1-я производная сглаженного ECDF будет все более беспристрастной для PDF.

Используйте с осторожностью:

• Вы должны сами выбрать количество узлов;
• производная НЕ нормализуется, так что площадь под кривой равна 1;
• результат может быть довольно нестабильным и подходит только для большого размера выборки.

аргументы функции:

• x: вектор образцов;
• n.knots: количество узлов;
• n.cells: количество точек сетки при построении производной функции

Вам необходимо установить scam пакет от CRAN.

library(scam)

test <- function (x, n.knots, n.cells) {

  ## get ECDF
  n <- length(x)
  x <- sort(x)
  y <- 1:n / n
  dat <- data.frame(x = x, y = y)  ## make sure `scam` can find `x` and `y`

  ## fit a monotonically increasing P-spline for ECDF
  fit <- scam::scam(y ~ s(x, bs = "mpi", k = n.knots), data = dat,
                    weights = c(n, rep(1, n - 2), 10 * n))
  ## interior knots
  xk <- with(fit$smooth[[1]], knots[4:(length(knots) - 3)])
  ## spline values at interior knots
  yk <- predict(fit, newdata = data.frame(x = xk))
  ## reparametrization into a monotone interpolation spline
  f <- stats::splinefun(xk, yk, "hyman")

  par(mfrow = c(1, 2))

  plot(x, y, pch = 19, col = "gray")  ## ECDF
  lines(x, f(x), type = "l")          ## smoothed ECDF
  title(paste0("number of knots: ", n.knots,
               "\neffective degree of freedom: ", round(sum(fit$edf), 2)),
        cex.main = 0.8)

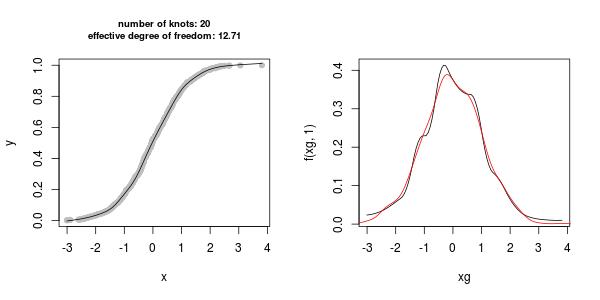
  xg <- seq(min(x), max(x), length = n.cells)
  plot(xg, f(xg, 1), type = "l")     ## density estimated by scam
  lines(stats::density(x), col = 2)  ## a proper density estimate by density

  ## return smooth ECDF function
  f
  }

---

## try large sample size
set.seed(1)
x <- rnorm(1000)
f <- test(x, n.knots = 20, n.cells = 100)

f это функция, возвращаемая stats::splinefun (читать ?splinefun).

Наивное, подобное решение состоит в том, чтобы сделать сплайн интерполяции на ECDF без сглаживания. Но это очень плохая идея, поскольку у нас нет последовательности.

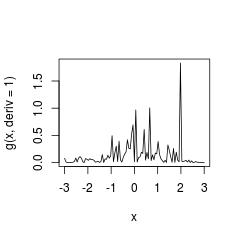
g <- splinefun(sort(x), 1:length(x) / length(x), method = "hyman")
curve(g(x, deriv = 1), from = -3, to = 3)

Напоминание: настоятельно рекомендуется использовать stats::density для прямой оценки плотности.