Python: простое объединение списков на основе пересечений

Question

Рассмотрим несколько списков целых чисел:

#--------------------------------------
0 [0,1,3]
1 [1,0,3,4,5,10,...]
2 [2,8]
3 [3,1,0,...]
...
n []
#--------------------------------------

Вопрос состоит в том, чтобы объединить списки, имеющие хотя бы один общий элемент. Таким образом, результаты только для данной части будут следующими:

#--------------------------------------
0 [0,1,3,4,5,10,...]
2 [2,8]
#--------------------------------------

Каков наиболее эффективный способ сделать это для больших данных (элементы - это просто числа)? Является tree структурировать что-то для размышления? Я делаю работу сейчас, преобразовывая списки в sets и итерации для пересечений, но это медленно! Кроме того, у меня такое ощущение, что это так элементарно! Кроме того, в реализации чего-то не хватает (неизвестно), потому что некоторые списки иногда остаются не объединенными! Сказав это, если вы предлагаете самореализацию, пожалуйста, будьте щедрыми и предоставьте простой пример кода [очевидно, Python - мой фаворит:)] или псевдокод.
Обновление 1: вот код, который я использовал:

#--------------------------------------
lsts = [[0,1,3],
        [1,0,3,4,5,10,11],
        [2,8],
        [3,1,0,16]];
#--------------------------------------

Функция (глючит!!):

#--------------------------------------
def merge(lsts):
    sts = [set(l) for l in lsts]
    i = 0
    while i < len(sts):
        j = i+1
        while j < len(sts):
            if len(sts[i].intersection(sts[j])) > 0:
                sts[i] = sts[i].union(sts[j])
                sts.pop(j)
            else: j += 1                        #---corrected
        i += 1
    lst = [list(s) for s in sts]
    return lst
#--------------------------------------

Результат:

#--------------------------------------
>>> merge(lsts)
>>> [0, 1, 3, 4, 5, 10, 11, 16], [8, 2]]
#--------------------------------------

Обновление 2: по моему опыту, код, данный Никласом Баумстарком ниже, показал, что он немного быстрее для простых случаев. Еще не проверен метод, данный "Крючком", поскольку это совершенно другой подход (кстати, он кажется интересным). Процедура тестирования для всего этого может быть очень трудной или невозможной для обеспечения результатов. Реальный набор данных, который я буду использовать, настолько велик и сложен, что невозможно отследить любую ошибку, просто повторив. То есть я должен быть на 100% удовлетворен надежностью метода, прежде чем поместить его на место в большом коде в качестве модуля. Просто пока метод Никласа быстрее, и ответ для простых множеств, конечно, правильный.
Тем не менее, как я могу быть уверен, что он работает хорошо для большого набора данных? Так как я не смогу визуально отследить ошибки!

Обновление 3: обратите внимание, что надежность метода гораздо важнее, чем скорость для этой проблемы. Надеюсь, я смогу наконец-то перевести код Python в Fortran для максимальной производительности.

Обновление 4:
В этом посте много интересных моментов и щедро даных ответов, конструктивных комментариев. Я бы рекомендовал прочитать все внимательно. Пожалуйста, примите мою благодарность за развитие вопроса, удивительные ответы и конструктивные комментарии и обсуждения.

Answer 1

Моя попытка:

def merge(lsts):
    sets = [set(lst) for lst in lsts if lst]
    merged = True
    while merged:
        merged = False
        results = []
        while sets:
            common, rest = sets[0], sets[1:]
            sets = []
            for x in rest:
                if x.isdisjoint(common):
                    sets.append(x)
                else:
                    merged = True
                    common |= x
            results.append(common)
        sets = results
    return sets

lst = [[65, 17, 5, 30, 79, 56, 48, 62],
       [6, 97, 32, 93, 55, 14, 70, 32],
       [75, 37, 83, 34, 9, 19, 14, 64],
       [43, 71],
       [],
       [89, 49, 1, 30, 28, 3, 63],
       [35, 21, 68, 94, 57, 94, 9, 3],
       [16],
       [29, 9, 97, 43],
       [17, 63, 24]]
print merge(lst)

Ориентир:

import random

# adapt parameters to your own usage scenario
class_count = 50
class_size = 1000
list_count_per_class = 100
large_list_sizes = list(range(100, 1000))
small_list_sizes = list(range(0, 100))
large_list_probability = 0.5

if False:  # change to true to generate the test data file (takes a while)
    with open("/tmp/test.txt", "w") as f:
        lists = []
        classes = [
            range(class_size * i, class_size * (i + 1)) for i in range(class_count)
        ]
        for c in classes:
            # distribute each class across ~300 lists
            for i in xrange(list_count_per_class):
                lst = []
                if random.random() < large_list_probability:
                    size = random.choice(large_list_sizes)
                else:
                    size = random.choice(small_list_sizes)
                nums = set(c)
                for j in xrange(size):
                    x = random.choice(list(nums))
                    lst.append(x)
                    nums.remove(x)
                random.shuffle(lst)
                lists.append(lst)
        random.shuffle(lists)
        for lst in lists:
            f.write(" ".join(str(x) for x in lst) + "\n")

setup = """
# Niklas'
def merge_niklas(lsts):
    sets = [set(lst) for lst in lsts if lst]
    merged = 1
    while merged:
        merged = 0
        results = []
        while sets:
            common, rest = sets[0], sets[1:]
            sets = []
            for x in rest:
                if x.isdisjoint(common):
                    sets.append(x)
                else:
                    merged = 1
                    common |= x
            results.append(common)
        sets = results
    return sets

# Rik's
def merge_rik(data):
    sets = (set(e) for e in data if e)
    results = [next(sets)]
    for e_set in sets:
        to_update = []
        for i, res in enumerate(results):
            if not e_set.isdisjoint(res):
                to_update.insert(0, i)

        if not to_update:
            results.append(e_set)
        else:
            last = results[to_update.pop(-1)]
            for i in to_update:
                last |= results[i]
                del results[i]
            last |= e_set
    return results

# katrielalex's
def pairs(lst):
    i = iter(lst)
    first = prev = item = i.next()
    for item in i:
        yield prev, item
        prev = item
    yield item, first

import networkx

def merge_katrielalex(lsts):
    g = networkx.Graph()
    for lst in lsts:
        for edge in pairs(lst):
            g.add_edge(*edge)
    return networkx.connected_components(g)

# agf's (optimized)
from collections import deque

def merge_agf_optimized(lists):
    sets = deque(set(lst) for lst in lists if lst)
    results = []
    disjoint = 0
    current = sets.pop()
    while True:
        merged = False
        newsets = deque()
        for _ in xrange(disjoint, len(sets)):
            this = sets.pop()
            if not current.isdisjoint(this):
                current.update(this)
                merged = True
                disjoint = 0
            else:
                newsets.append(this)
                disjoint += 1
        if sets:
            newsets.extendleft(sets)
        if not merged:
            results.append(current)
            try:
                current = newsets.pop()
            except IndexError:
                break
            disjoint = 0
        sets = newsets
    return results

# agf's (simple)
def merge_agf_simple(lists):
    newsets, sets = [set(lst) for lst in lists if lst], []
    while len(sets) != len(newsets):
        sets, newsets = newsets, []
        for aset in sets:
            for eachset in newsets:
                if not aset.isdisjoint(eachset):
                    eachset.update(aset)
                    break
            else:
                newsets.append(aset)
    return newsets

# alexis'
def merge_alexis(data):
    bins = range(len(data))  # Initialize each bin[n] == n
    nums = dict()

    data = [set(m) for m in data]  # Convert to sets
    for r, row in enumerate(data):
        for num in row:
            if num not in nums:
                # New number: tag it with a pointer to this row's bin
                nums[num] = r
                continue
            else:
                dest = locatebin(bins, nums[num])
                if dest == r:
                    continue  # already in the same bin

                if dest > r:
                    dest, r = r, dest  # always merge into the smallest bin

                data[dest].update(data[r])
                data[r] = None
                # Update our indices to reflect the move
                bins[r] = dest
                r = dest

    # Filter out the empty bins
    have = [m for m in data if m]
    return have

def locatebin(bins, n):
    while bins[n] != n:
        n = bins[n]
    return n

lsts = []
size = 0
num = 0
max = 0
for line in open("/tmp/test.txt", "r"):
    lst = [int(x) for x in line.split()]
    size += len(lst)
    if len(lst) > max:
        max = len(lst)
    num += 1
    lsts.append(lst)
"""

setup += """
print "%i lists, {class_count} equally distributed classes, average size %i, max size %i" % (num, size/num, max)
""".format(class_count=class_count)

import timeit
print "niklas"
print timeit.timeit("merge_niklas(lsts)", setup=setup, number=3)
print "rik"
print timeit.timeit("merge_rik(lsts)", setup=setup, number=3)
print "katrielalex"
print timeit.timeit("merge_katrielalex(lsts)", setup=setup, number=3)
print "agf (1)"
print timeit.timeit("merge_agf_optimized(lsts)", setup=setup, number=3)
print "agf (2)"
print timeit.timeit("merge_agf_simple(lsts)", setup=setup, number=3)
print "alexis"
print timeit.timeit("merge_alexis(lsts)", setup=setup, number=3)

Эти временные интервалы, очевидно, зависят от конкретных параметров эталонного теста, таких как количество классов, количество списков, размер списка и т. Д. Адаптируйте эти параметры в соответствии с вашими потребностями для получения более полезных результатов.

Ниже приведены примеры выходных данных на моей машине для различных параметров. Они показывают, что все алгоритмы имеют свои сильные и слабые стороны, в зависимости от вида входных данных, которые они получают:

=====================
# many disjoint classes, large lists
class_count = 50
class_size = 1000
list_count_per_class = 100
large_list_sizes = list(range(100, 1000))
small_list_sizes = list(range(0, 100))
large_list_probability = 0.5
=====================

niklas
5000 lists, 50 equally distributed classes, average size 298, max size 999
4.80084705353
rik
5000 lists, 50 equally distributed classes, average size 298, max size 999
9.49251699448
katrielalex
5000 lists, 50 equally distributed classes, average size 298, max size 999
21.5317108631
agf (1)
5000 lists, 50 equally distributed classes, average size 298, max size 999
8.61671280861
agf (2)
5000 lists, 50 equally distributed classes, average size 298, max size 999
5.18117713928
=> alexis
=> 5000 lists, 50 equally distributed classes, average size 298, max size 999
=> 3.73504281044

===================
# less number of classes, large lists
class_count = 15
class_size = 1000
list_count_per_class = 300
large_list_sizes = list(range(100, 1000))
small_list_sizes = list(range(0, 100))
large_list_probability = 0.5
===================

niklas
4500 lists, 15 equally distributed classes, average size 296, max size 999
1.79993700981
rik
4500 lists, 15 equally distributed classes, average size 296, max size 999
2.58237695694
katrielalex
4500 lists, 15 equally distributed classes, average size 296, max size 999
19.5465381145
agf (1)
4500 lists, 15 equally distributed classes, average size 296, max size 999
2.75445604324
=> agf (2)
=> 4500 lists, 15 equally distributed classes, average size 296, max size 999
=> 1.77850699425
alexis
4500 lists, 15 equally distributed classes, average size 296, max size 999
3.23530197144

===================
# less number of classes, smaller lists
class_count = 15
class_size = 1000
list_count_per_class = 300
large_list_sizes = list(range(100, 1000))
small_list_sizes = list(range(0, 100))
large_list_probability = 0.1
===================

niklas
4500 lists, 15 equally distributed classes, average size 95, max size 997
0.773697137833
rik
4500 lists, 15 equally distributed classes, average size 95, max size 997
1.0523750782
katrielalex
4500 lists, 15 equally distributed classes, average size 95, max size 997
6.04466891289
agf (1)
4500 lists, 15 equally distributed classes, average size 95, max size 997
1.20285701752
=> agf (2)
=> 4500 lists, 15 equally distributed classes, average size 95, max size 997
=> 0.714507102966
alexis
4500 lists, 15 equally distributed classes, average size 95, max size 997
1.1286110878

Answer 2

Я попытался суммировать все, что было сказано и сделано по этой теме в этом вопросе и в дубликате.

Я попытался проверить и время каждого решения (весь код здесь).

тестирование

Это TestCase из модуля тестирования:

class MergeTestCase(unittest.TestCase):

    def setUp(self):
        with open('./lists/test_list.txt') as f:
            self.lsts = json.loads(f.read())
        self.merged = self.merge_func(deepcopy(self.lsts))

    def test_disjoint(self):
        """Check disjoint-ness of merged results"""
        from itertools import combinations
        for a,b in combinations(self.merged, 2):
            self.assertTrue(a.isdisjoint(b))

    def test_coverage(self):    # Credit to katrielalex
        """Check coverage original data"""
        merged_flat = set()
        for s in self.merged:
            merged_flat |= s

        original_flat = set()
        for lst in self.lsts:
            original_flat |= set(lst)

        self.assertTrue(merged_flat == original_flat)

    def test_subset(self):      # Credit to WolframH
        """Check that every original data is a subset"""
        for lst in self.lsts:
            self.assertTrue(any(set(lst) <= e for e in self.merged))

Этот тест предполагает список наборов в качестве результата, поэтому я не смог протестировать пару решений, которые работали со списками.

Я не мог проверить следующее:

katrielalex
steabert

Среди тех, что я мог проверить, два не удалось:

  -- Going to test: agf (optimized) --
Check disjoint-ness of merged results ... FAIL

  -- Going to test: robert king --
Check disjoint-ness of merged results ... FAIL

тайминг

Показатели тесно связаны с используемым тестом данных.

До сих пор три ответа пытались найти время для своего и других решений. Поскольку они использовали разные данные тестирования, у них были разные результаты.

1. Тест Niklas очень настраиваемый. С его бенчмарком можно было делать разные тесты, меняя некоторые параметры.

   Я использовал те же три набора параметров, которые он использовал в своем собственном ответе, и поместил их в три разных файла:

   filename = './lists/timing_1.txt'
   class_count = 50,
   class_size = 1000,
   list_count_per_class = 100,
   large_list_sizes = (100, 1000),
   small_list_sizes = (0, 100),
   large_list_probability = 0.5,
   
   filename = './lists/timing_2.txt'
   class_count = 15,
   class_size = 1000,
   list_count_per_class = 300,
   large_list_sizes = (100, 1000),
   small_list_sizes = (0, 100),
   large_list_probability = 0.5,
   
   filename = './lists/timing_3.txt'
   class_count = 15,
   class_size = 1000,
   list_count_per_class = 300,
   large_list_sizes = (100, 1000),
   small_list_sizes = (0, 100),
   large_list_probability = 0.1,
   

   Вот результаты, которые я получил:

   Из файла: timing_1.txt

   Timing with: >> Niklas << Benchmark
   Info: 5000 lists, average size 305, max size 999
   
   Timing Results:
   10.434  -- alexis
   11.476  -- agf
   11.555  -- Niklas B.
   13.622  -- Rik. Poggi
   14.016  -- agf (optimized)
   14.057  -- ChessMaster
   20.208  -- katrielalex
   21.697  -- steabert
   25.101  -- robert king
   76.870  -- Sven Marnach
   133.399  -- hochl
   

   Из файла: timing_2.txt

   Timing with: >> Niklas << Benchmark
   Info: 4500 lists, average size 305, max size 999
   
   Timing Results:
   8.247  -- Niklas B.
   8.286  -- agf
   8.637  -- Rik. Poggi
   8.967  -- alexis
   9.090  -- ChessMaster
   9.091  -- agf (optimized)
   18.186  -- katrielalex
   19.543  -- steabert
   22.852  -- robert king
   70.486  -- Sven Marnach
   104.405  -- hochl
   

   Из файла: timing_3.txt

   Timing with: >> Niklas << Benchmark
   Info: 4500 lists, average size 98, max size 999
   
   Timing Results:
   2.746  -- agf
   2.850  -- Niklas B.
   2.887  -- Rik. Poggi
   2.972  -- alexis
   3.077  -- ChessMaster
   3.174  -- agf (optimized)
   5.811  -- katrielalex
   7.208  -- robert king
   9.193  -- steabert
   23.536  -- Sven Marnach
   37.436  -- hochl
   

2. С данными тестирования Свена я получил следующие результаты:

   Timing with: >> Sven << Benchmark
   Info: 200 lists, average size 10, max size 10
   
   Timing Results:
   2.053  -- alexis
   2.199  -- ChessMaster
   2.410  -- agf (optimized)
   3.394  -- agf
   3.398  -- Rik. Poggi
   3.640  -- robert king
   3.719  -- steabert
   3.776  -- Niklas B.
   3.888  -- hochl
   4.610  -- Sven Marnach
   5.018  -- katrielalex
   

3. И, наконец, с тестом Agf я получил:

   Timing with: >> Agf << Benchmark
   Info: 2000 lists, average size 246, max size 500
   
   Timing Results:
   3.446  -- Rik. Poggi
   3.500  -- ChessMaster
   3.520  -- agf (optimized)
   3.527  -- Niklas B.
   3.527  -- agf
   3.902  -- hochl
   5.080  -- alexis
   15.997  -- steabert
   16.422  -- katrielalex
   18.317  -- robert king
   1257.152  -- Sven Marnach
   

Как я сказал в начале, весь код доступен в этом репозитории git. Все функции слияния находятся в файле с именем core.pyкаждая функция с именем, заканчивающимся на _merge будет автоматически загружаться во время тестов, поэтому не составит труда добавить / протестировать / улучшить собственное решение.

Дайте мне также знать, если что-то не так, это было много кодирования, и я мог бы использовать пару свежих глаз:)

Answer 3

Использование матричных манипуляций

Позвольте мне предвосхитить этот ответ следующим комментарием:

ЭТО НЕПРАВИЛЬНЫЙ СПОСОБ ЭТОГО. ЭТО НЕСКОЛЬКО ЧИСЛЕННОЙ НЕУСТОЙЧИВОСТИ И МНОГО МЕНЬШЕ, ЧЕМ ПРЕДСТАВЛЕНЫ ДРУГИЕ МЕТОДЫ, ИСПОЛЬЗУЙТЕ НА СВОЙ СТРАХ И РИСК.

При этом я не смог устоять перед решением проблемы с динамической точки зрения (и я надеюсь, что вы получите свежий взгляд на проблему). Теоретически это должно работать все время, но вычисления собственных значений часто могут потерпеть неудачу. Идея состоит в том, чтобы думать о вашем списке как о потоке строк и столбцов. Если две строки имеют общее значение, между ними существует связующий поток. Если бы мы думали об этих потоках как о воде, мы бы увидели, что потоки группируются в маленькие бассейны, когда между ними существует связующий путь. Для простоты я собираюсь использовать меньший набор, хотя он также работает с вашим набором данных:

from numpy import where, newaxis
from scipy import linalg, array, zeros

X = [[0,1,3],[2],[3,1]]

Нам нужно преобразовать данные в потоковый график. Если строка i переходит в значение j, мы помещаем его в матрицу. Здесь у нас есть 3 строки и 4 уникальных значения:

A = zeros((4,len(X)), dtype=float)
for i,row in enumerate(X):
    for val in row: A[val,i] = 1

В общем, вам нужно изменить 4 чтобы захватить количество уникальных значений у вас есть. Если набор представляет собой список целых чисел, начиная с 0, как у нас, вы можете просто сделать это наибольшее число. Теперь выполним разложение по собственным значениям. Точнее SVD, так как наша матрица не квадратная.

S  = linalg.svd(A)

Мы хотим оставить только 3х3 часть этого ответа, так как он будет представлять поток пулов. На самом деле мы хотим только абсолютные значения этой матрицы; мы заботимся только о наличии потока в этом кластерном пространстве.

M  = abs(S[2])

Мы можем думать об этой матрице M как о марковской матрице и делать ее явной посредством нормализации строк. Как только мы получим это, мы вычисляем декомпозицию собственного значения (слева). этой матрицы.

M /=  M.sum(axis=1)[:,newaxis]
U,V = linalg.eig(M,left=True, right=False)
V = abs(V)

Теперь несвязная (неэргодическая) марковская матрица обладает хорошим свойством, что для каждого несвязного кластера существует собственное значение единицы. Собственные векторы, связанные с этими значениями единства, - это те, которые мы хотим:

idx = where(U > .999)[0]
C = V.T[idx] > 0

Я должен использовать.999 из-за вышеупомянутой численной нестабильности. На этом мы закончили! Каждый независимый кластер может теперь вытянуть соответствующие строки:

for cluster in C:
    print where(A[:,cluster].sum(axis=1))[0]

Что дает, как и предполагалось:

[0 1 3]
[2]

+ Изменить X на ваш lst и вы получите: [ 0 1 3 4 5 10 11 16] [2 8],

---

добавление

Почему это может быть полезно? Я не знаю, откуда берутся ваши базовые данные, но что происходит, когда соединения не абсолютны? Скажи ряд 1 есть запись 3 80% времени - как бы вы обобщили проблему? Приведенный выше метод потока будет работать нормально и будет полностью параметризован .999 ценность, чем дальше от единства, тем слабее ассоциация.

---

Визуальное представление

Поскольку картинка стоит 1 тыс. Слов, вот графики матриц A и V для моего примера и вашей lst соответственно. Обратите внимание, как в V разбивается на два кластера (это блок-диагональная матрица с двумя блоками после перестановки), поскольку для каждого примера было только два уникальных списка!

---

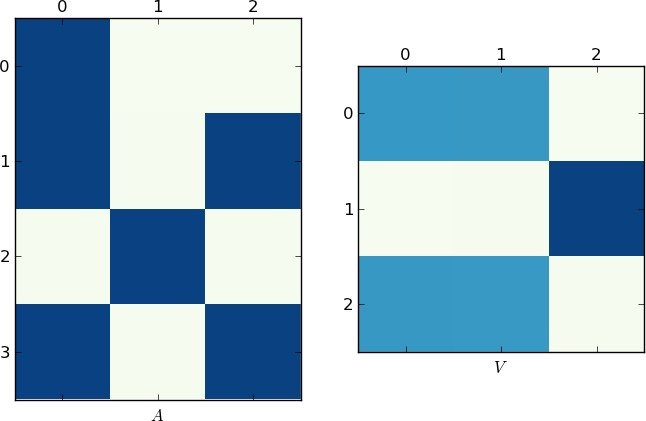
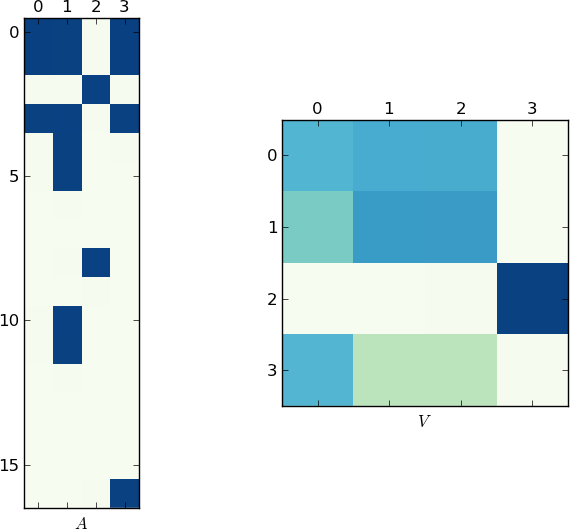
Быстрая реализация

Оглядываясь назад, я понял, что вы можете пропустить шаг SVD и вычислить только одну распаковку:

M = dot(A.T,A)
M /=  M.sum(axis=1)[:,newaxis]
U,V = linalg.eig(M,left=True, right=False)

Преимущество этого метода (помимо скорости) заключается в том, что M теперь симметричен, следовательно, вычисления могут быть более быстрыми и более точными (без мнимых значений, о которых нужно беспокоиться).

Answer 4

РЕДАКТИРОВАТЬ: ОК, другие вопросы были закрыты, размещение здесь.

Хороший вопрос! Намного проще, если вы думаете о ней как о проблеме связанных компонентов в графе. Следующий код использует отличный networkx библиотека графов и pairs Функция из этого вопроса.

def pairs(lst):
    i = iter(lst)
    first = prev = item = i.next()
    for item in i:
        yield prev, item
        prev = item
    yield item, first

lists = [[1,2,3],[3,5,6],[8,9,10],[11,12,13]]

import networkx
g = networkx.Graph()
for sub_list in lists:
    for edge in pairs(sub_list):
            g.add_edge(*edge)

networkx.connected_components(g)
[[1, 2, 3, 5, 6], [8, 9, 10], [11, 12, 13]]

---

объяснение

Создаем новый (пустой) график g, Для каждого подсписка в lists, рассмотреть его элементы как узлы графа и добавить ребро между ними. (Поскольку нас заботит только связность, нам не нужно добавлять все ребра - только соседние!) Обратите внимание, что add_edge берет два объекта, обрабатывает их как узлы (и добавляет их, если их там еще нет) и добавляет грань между ними.

Тогда мы просто находим связные компоненты графа - решенная проблема! - и вывести их как наши пересекающиеся множества.

Answer 5

Вот мой ответ. Я не проверял это с сегодняшней партией ответов.

Алгоритмы, основанные на пересечении, - это O(N^2), поскольку они проверяют каждый новый набор на соответствие всем существующим, поэтому я использовал подход, который индексирует каждое число и работает близко к O(N) (если мы примем, что поиск в словаре O(1)). Затем я провел тесты и почувствовал себя полным идиотом, потому что он работал медленнее, но при ближайшем рассмотрении оказалось, что тестовые данные заканчиваются лишь несколькими отличными наборами результатов, поэтому квадратичным алгоритмам не нужно много работать для делать. Протестируйте его с более чем 10-15 различными бинами, и мой алгоритм намного быстрее. Попробуйте тестовые данные с более чем 50 различными бинами, и это будет чрезвычайно быстро.

(Редактировать: была также проблема с тем, как выполняется тест, но я ошибся в своем диагнозе. Я изменил свой код, чтобы он работал так, как выполняются повторные тесты).

def mergelists5(data):
    """Check each number in our arrays only once, merging when we find
    a number we have seen before.
    """

    bins = range(len(data))  # Initialize each bin[n] == n
    nums = dict()

    data = [set(m) for m in data ]  # Convert to sets    
    for r, row in enumerate(data):
        for num in row:
            if num not in nums:
                # New number: tag it with a pointer to this row's bin
                nums[num] = r
                continue
            else:
                dest = locatebin(bins, nums[num])
                if dest == r:
                    continue # already in the same bin

                if dest > r:
                    dest, r = r, dest   # always merge into the smallest bin

                data[dest].update(data[r]) 
                data[r] = None
                # Update our indices to reflect the move
                bins[r] = dest
                r = dest 

    # Filter out the empty bins
    have = [ m for m in data if m ]
    print len(have), "groups in result"
    return have


def locatebin(bins, n):
    """
    Find the bin where list n has ended up: Follow bin references until
    we find a bin that has not moved.
    """
    while bins[n] != n:
        n = bins[n]
    return n

Answer 6

Эта новая функция выполняет только минимально необходимое количество тестов на дизъюнктность, чего не могут сделать другие подобные решения. Он также использует deque чтобы избежать как можно большего количества операций с линейным временем, таких как нарезка и удаление списка с самого начала списка.

from collections import deque

def merge(lists):
    sets = deque(set(lst) for lst in lists if lst)
    results = []
    disjoint = 0
    current = sets.pop()
    while True:
        merged = False
        newsets = deque()
        for _ in xrange(disjoint, len(sets)):
            this = sets.pop()
            if not current.isdisjoint(this):
                current.update(this)
                merged = True
                disjoint = 0
            else:
                newsets.append(this)
                disjoint += 1
        if sets:
            newsets.extendleft(sets)
        if not merged:
            results.append(current)
            try:
                current = newsets.pop()
            except IndexError:
                break
            disjoint = 0
        sets = newsets
    return results

Чем меньше совпадений между наборами в данном наборе данных, тем лучше это будет по сравнению с другими функциями.

Вот пример случая. Если у вас 4 комплекта, вам нужно сравнить:

1, 2
1, 3
1, 4
2, 3
2, 4
3, 4

Если 1 пересекается с 3, то 2 необходимо повторно протестировать, чтобы увидеть, не пересекается ли теперь с 1, чтобы безопасно пропустить тестирование 2 против 3.

Есть два способа справиться с этим. Первый - это перезапустить тестирование набора 1 по отношению к другим наборам после каждого перекрытия и слияния. Второе - продолжить тестирование, сравнив 1 с 4, затем вернувшись назад и повторно протестировав. Последнее приводит к меньшему количеству тестов дизъюнктности, так как за один проход происходит больше слияний, поэтому при повторном тестировании остается меньше наборов для тестирования.

Проблема состоит в том, чтобы отследить, какие наборы должны быть повторно протестированы. В приведенном выше примере 1 необходимо повторно протестировать против 2, но не против 4, поскольку 1 уже был в своем текущем состоянии, прежде чем 4 был протестирован в первый раз.

disjoint Счетчик позволяет отслеживать это.

---

Мой ответ не помогает с основной проблемой поиска улучшенного алгоритма перекодирования в FORTRAN; это как раз то, что мне кажется самым простым и элегантным способом реализации алгоритма в Python.

Согласно моему тестированию (или тесту в принятом ответе), оно немного (до 10%) быстрее, чем следующее быстрое решение.

def merge0(lists):
    newsets, sets = [set(lst) for lst in lists if lst], []
    while len(sets) != len(newsets):
        sets, newsets = newsets, []
        for aset in sets:
            for eachset in newsets:
                if not aset.isdisjoint(eachset):
                    eachset.update(aset)
                    break
            else:
                newsets.append(aset)
    return newsets

Нет необходимости в непифоновых счетчиках (i, range) или сложная мутация (del, pop, insert) используется в других реализациях. Он использует только простую итерацию, объединяет перекрывающиеся наборы самым простым способом и создает один новый список при каждом прохождении данных.

Моя (более быстрая и простая) версия тестового кода:

import random

tenk = range(10000)
lsts = [random.sample(tenk, random.randint(0, 500)) for _ in range(2000)]

setup = """
def merge0(lists):
  newsets, sets = [set(lst) for lst in lists if lst], []
  while len(sets) != len(newsets):
    sets, newsets = newsets, []
    for aset in sets:
      for eachset in newsets:
        if not aset.isdisjoint(eachset):
          eachset.update(aset)
          break
      else:
        newsets.append(aset)
  return newsets

def merge1(lsts):
  sets = [set(lst) for lst in lsts if lst]
  merged = 1
  while merged:
    merged = 0
    results = []
    while sets:
      common, rest = sets[0], sets[1:]
      sets = []
      for x in rest:
        if x.isdisjoint(common):
          sets.append(x)
        else:
          merged = 1
          common |= x
      results.append(common)
    sets = results
  return sets

lsts = """ + repr(lsts)

import timeit
print timeit.timeit("merge0(lsts)", setup=setup, number=10)
print timeit.timeit("merge1(lsts)", setup=setup, number=10)

Answer 7

Вот реализация, использующая структуру данных с непересекающимися наборами (в частности, непересекающийся лес), благодаря подсказке comestorm о слиянии множеств, у которых есть хотя бы один общий элемент. Я использую сжатие пути для небольшого (~5%) улучшения скорости; это не совсем необходимо (и это мешает find будучи хвостом рекурсивным, что может замедлить ход событий). Обратите внимание, что я использую dict представлять непересекающийся лес; учитывая, что данные int s, массив также будет работать, хотя он может быть не намного быстрее.

def merge(data):
    parents = {}
    def find(i):
        j = parents.get(i, i)
        if j == i:
            return i
        k = find(j)
        if k != j:
            parents[i] = k
        return k
    for l in filter(None, data):
        parents.update(dict.fromkeys(map(find, l), find(l[0])))
    merged = {}
    for k, v in parents.items():
        merged.setdefault(find(v), []).append(k)
    return merged.values()

Этот подход сопоставим с другими лучшими алгоритмами в тестах Рика.

Answer 8

Это был бы мой обновленный подход:

def merge(data):
    sets = (set(e) for e in data if e)
    results = [next(sets)]
    for e_set in sets:
        to_update = []
        for i,res in enumerate(results):
            if not e_set.isdisjoint(res):
                to_update.insert(0,i)

        if not to_update:
            results.append(e_set)
        else:
            last = results[to_update.pop(-1)]
            for i in to_update:
                last |= results[i]
                del results[i]
            last |= e_set

    return results

Примечание. При объединении пустые списки будут удалены.

Обновление: надежность.

Вам нужны два теста для 100% надежности успеха:

• Убедитесь, что все результирующие множества не связаны друг с другом:

  merged = [{0, 1, 3, 4, 5, 10, 11, 16}, {8, 2}, {8}]
  
  from itertools import combinations
  for a,b in combinations(merged,2):
      if not a.isdisjoint(b):
          raise Exception(a,b)    # just an example
  

• Убедитесь, что объединенный набор охватывает исходные данные. (как предложено katrielalex)

Я думаю, что это займет некоторое время, но, возможно, оно того стоит, если вы хотите быть на 100% уверены.

Answer 9

Просто для удовольствия...

def merge(mylists):
    results, sets = [], [set(lst) for lst in mylists if lst]
    upd, isd, pop = set.update, set.isdisjoint, sets.pop
    while sets:
        if not [upd(sets[0],pop(i)) for i in xrange(len(sets)-1,0,-1) if not isd(sets[0],sets[i])]:
            results.append(pop(0))
    return results

и мой переписать лучший ответ

def merge(lsts):
  sets = map(set,lsts)
  results = []
  while sets:
    first, rest = sets[0], sets[1:]
    merged = False
    sets = []
    for s in rest:
      if s and s.isdisjoint(first):
        sets.append(s)
      else:
        first |= s
        merged = True
    if merged: sets.append(first)
    else: results.append(first)
  return results

Answer 10

Это медленнее, чем решение, предлагаемое Никласом (я получил 3,9 с на test.txt вместо 0,5 с для его решения), но дает тот же результат и может быть легче реализовать, например, в Fortran, поскольку он не использует наборы, только сортировка по общему количеству элементов, а затем один проход через все из них.

Он возвращает список с идентификаторами объединенных списков, поэтому также отслеживает пустые списки, они остаются не объединенными.

def merge(lsts):
        # this is an index list that stores the joined id for each list
        joined = range(len(lsts))
        # create an ordered list with indices
        indexed_list = sorted((el,index) for index,lst in enumerate(lsts) for el in lst)
        # loop throught the ordered list, and if two elements are the same and
        # the lists are not yet joined, alter the list with joined id
        el_0,idx_0 = None,None
        for el,idx in indexed_list:
                if el == el_0 and joined[idx] != joined[idx_0]:
                        old = joined[idx]
                        rep = joined[idx_0]
                        joined = [rep if id == old else id for id in joined]
                el_0, idx_0 = el, idx
        return joined

Answer 11

lists = [[1,2,3],[3,5,6],[8,9,10],[11,12,13]]

import networkx as nx
g = nx.Graph()

for sub_list in lists:
    for i in range(1,len(sub_list)):
        g.add_edge(sub_list[0],sub_list[i])

print nx.connected_components(g)
#[[1, 2, 3, 5, 6], [8, 9, 10], [11, 12, 13]]

Спектакль:

5000 lists, 5 classes, average size 74, max size 1000
15.2264976415

Производительность слияния1:

print timeit.timeit("merge1(lsts)", setup=setup, number=10)
5000 lists, 5 classes, average size 74, max size 1000
1.26998780571

Так что это в 11 раз медленнее, чем самый быстрый... но код гораздо проще и удобочитаемее!

Answer 12

Вот функция (Python 3.1), чтобы проверить, в порядке ли результат функции слияния. Это проверяет:

• Являются ли результирующие наборы непересекающимися? (количество элементов объединения == сумма номеров элементов)
• Элементы набора результатов совпадают со списками ввода?
• Является ли каждый входной список подмножеством набора результатов?
• Является ли каждый набор результатов минимальным, т. Е. Невозможно ли разбить его на два меньших набора?
• Он не проверяет, есть ли пустые наборы результатов - я не знаю, хотите вы их или нет...

,

from itertools import chain

def check(lsts, result):
    lsts = [set(s) for s in lsts]
    all_items = set(chain(*lsts))
    all_result_items = set(chain(*result))
    num_result_items = sum(len(s) for s in result)
    if num_result_items != len(all_result_items):
        print("Error: result sets overlap!")
        print(num_result_items, len(all_result_items))
        print(sorted(map(len, result)), sorted(map(len, lsts)))
    if all_items != all_result_items:
        print("Error: result doesn't match input lists!")
    if not all(any(set(s).issubset(t) for t in result) for s in lst):
        print("Error: not all input lists are contained in a result set!")

    seen = set()
    todo = list(filter(bool, lsts))
    done = False
    while not done:
        deletes = []
        for i, s in enumerate(todo): # intersection with seen, or with unseen result set, is OK
            if not s.isdisjoint(seen) or any(t.isdisjoint(seen) for t in result if not s.isdisjoint(t)):
                seen.update(s)
                deletes.append(i)
        for i in reversed(deletes):
            del todo[i]
        done = not deletes
    if todo:
        print("Error: A result set should be split into two or more parts!")
        print(todo)

Answer 13

Во-первых, я не совсем уверен, что критерии справедливы:

Добавление следующего кода в начало моей функции:

c = Counter(chain(*lists))
    print c[1]
"88"

Это означает, что из всех значений во всех списках есть только 88 различных значений. Обычно в реальном мире дубликаты встречаются редко, и вы ожидаете гораздо более четких значений. (конечно, я не знаю, откуда ваши данные, поэтому не могу делать предположения).

Поскольку дубликаты встречаются чаще, это означает, что наборы с меньшей вероятностью будут непересекающимися. Это означает, что метод set.isdisjoint() будет намного быстрее, потому что только после нескольких тестов он обнаружит, что наборы не пересекаются.

Сказав все это, я считаю, что представленные методы, использующие дизъюнкт, являются самыми быстрыми в любом случае, но я просто говорю, что вместо того, чтобы быть в 20 раз быстрее, возможно, они должны быть только в 10 раз быстрее, чем другие методы с другим тестированием производительности.

В любом случае, я подумал, что попробую немного другую технику, чтобы решить эту проблему, однако сортировка слиянием была слишком медленной, этот метод примерно в 20 раз медленнее, чем два самых быстрых метода, использующих бенчмаркинг:

Я думал, что закажу все

import heapq
from itertools import chain
def merge6(lists):
    for l in lists:
        l.sort()
    one_list = heapq.merge(*[zip(l,[i]*len(l)) for i,l in enumerate(lists)]) #iterating through one_list takes 25 seconds!!
    previous = one_list.next()

    d = {i:i for i in range(len(lists))}
    for current in one_list:
        if current[0]==previous[0]:
            d[current[1]] = d[previous[1]]
        previous=current

    groups=[[] for i in range(len(lists))]
    for k in d:
        groups[d[k]].append(lists[k]) #add a each list to its group

    return [set(chain(*g)) for g in groups if g] #since each subroup in each g is sorted, it would be faster to merge these subgroups removing duplicates along the way.


lists = [[1,2,3],[3,5,6],[8,9,10],[11,12,13]]
print merge6(lists)
"[set([1, 2, 3, 5, 6]), set([8, 9, 10]), set([11, 12, 13])]""



import timeit
print timeit.timeit("merge1(lsts)", setup=setup, number=10)
print timeit.timeit("merge4(lsts)", setup=setup, number=10)
print timeit.timeit("merge6(lsts)", setup=setup, number=10)
5000 lists, 5 classes, average size 74, max size 1000
1.26732238315
5000 lists, 5 classes, average size 74, max size 1000
1.16062907437
5000 lists, 5 classes, average size 74, max size 1000
30.7257182826

Answer 14

Я нашел ответ @Niklas B. действительно полезным ... но мне потребовалось некоторое время, чтобы прочитать его и понять логику. Это переписывание точно такого же кода с новыми именами переменных и дополнительным объяснением... чтобы помочь другим N00bs!

      def mergeUntilOnlyDisjointSetsRemain(_listsOfLists):

    """Function for merging lists until there are only disjoint sets"""
    
    """Imagine this algorithm as if it were processing train cars filled with
    integers. It takes the first car of the train, separates it from the rest, 
    and then compares the first car to each subsequent car.
    Start by renaming the first car to 'common'
    If the two train cars have a common integer, you merge the two cars into
    common, and continue down the line until you reach the end of the train.
    Once you reach the end of the train, place the common car in results, (which
    is essentially a collection of train cars that have already been compared 
    to all other cars).
    You can exit the loop as soon as you get to the end of the train without
    merging any of the cars. This is controlled by the continueMerge variable.
    This variable is only reset to True after a merge operation.
    """

    # Start by creating a trainCar(i.e. a set) from each list in our listOfLists
    freightTrain = [set(trainCar) for trainCar in _listsOfLists if trainCar]

    # This continueMerge means that we have not yet compared all cars in the train.
    continueMerge = True
    while continueMerge:
        # Reset the while loop trigger.
        continueMerge = False
        # Create a fresh empty list of cars that have already been cross checked
        crossCheckedCars = []
        # While there are still elements in freightTrain
        while freightTrain:
            # Split the freightTrain up, into first car vs all the remaining cars
            commonFirstTrainCar = freightTrain[0]
            remainingCars = freightTrain[1:]
            # The freightTrain is now empty
            freightTrain = []
            # Iterate over all the remaining traincars
            for currentTrainCar in remainingCars:
                # If there are not any common integers with the first car...
                if currentTrainCar.isdisjoint(commonFirstTrainCar):
                    # Add each train car back onto the freightTrain
                    freightTrain.append(currentTrainCar)
                # But if they share a common integer...
                else:
                    # Trigger the reset switch to continueMerging cars
                    continueMerge = True
                    # and Join he cars together
                    commonFirstTrainCar |= currentTrainCar
            # Once we have checked commonFirstTrainCar, remove it from the 
            # freightTrain and place it in crossCheckedCars
            crossCheckedCars.append(commonFirstTrainCar)

        # Now we have compared the first car to all subsequent cars
        # (... but we aren't finished because the 5th and 7th cars might have
        # had a common integer with each other... but only 1st and 5th cars
        # shared an integer the first time around... so the 1st and 5th cars
        # were merged, but the 7th car is still alone!)

        # Reset the system by creating a new freightTrain
        freightTrain = crossCheckedCars

    # Post-process the freight train to turn it into lists instead of sets
    listsForReturnTripHome = []
    for processedTraincar in freightTrain:
        listsForReturnTripHome.append(list(processedTraincar))
    return listsForReturnTripHome

Answer 15

Сегодня мне понадобилась эта функция, и я наткнулся как на эту тему SO, так и на ее дубликат. Прежде всего, огромное спасибо всем, кто принял участие, особенно @alexis, чей ответ сильно повлиял на мой, и @Rik Poggi, чей репозиторий GitHub оказался чрезвычайно полезным для тестирования и оценки моей версии. Это такая тема, которая делает НАСТОЛЬКО бесценным!

Несколько примечаний:

• Я переработал репозиторий, чтобы переместить «deepcopy(lsts)» из резервного исполнения в установку. С использованиемtimeit.repeat, у нас точно такое же поведение и безопасность, ноdeepcopyне влияет на тайминги. Это объясняет, почему указанные ниже тайминги такие низкие.
• Я добавил в репозиторий скрипт профилировщика, поэтому, если вы добавите свою функцию, вы сможете легко профилировать ее по любому из списков.
• Моя вилка репозитория @Rik Poggi находится здесь.
• Как было сказано выше, моя версия представляет собой переработку ответа @alexis. Оба мы являемся производными от алгоритма поиска объединения, но основное отличие состоит в том, что моя версия обновляет все родительские узлы (bin_ref) при слиянии, а не только основного узла. Это позволяет мне избежать рекурсивного обхода дерева в ответе @alexis (locatebin), и я думаю, что это делает код более понятным.
• Это довольно непрозрачный способ сделать то, что мы хотим (если только вы не математик, а я нет), поэтому я постарался сделать код максимально читабельным. Я считаю, что в данном случае «читаемый» -> «поддерживаемый».
• Моя версия не делает слишком много предположений относительно входных данных. Мои требования былиlist[tuple[Path]], поэтому я сделал версию, в которой не слишком заботились о данных внутри. Пока вы проходитеIterable[Iterable[T]]гдеTхешируется, с вами все будет в порядке.

О результатах:

• Моя версия, кажется, лучше работает с большими наборами данных. Его производительность немного ниже (в худшем случае в 2,5 раза медленнее, чем в лучшем случае), поскольку наборы данных становятся меньше. Для наборов данных среднего размера отдайте предпочтение версии @Rik Poggi. Для наборов данных небольшого размера отдайте предпочтение версии @alexis.

      from itertools import chain
from typing import Iterable, TypeVar

T = TypeVar('T')


def merge_intersections(lists: Iterable[Iterable[T]]) -> list[set[T]]:
    """
    Merges lists based on whether or not they intersect. Returns a list
    of mutually disjoint sets.

    How it works:
    The general idea is to iterate over the sequences and merge them in
    their "intersection-bins". To do so, for each sequence, we look for
    items that were already encountered during previous iteration. If we
    don't find any, this means the current sequence might be disjoint
    from the rest, so we put it in its own bin. If, on the other hand,
    we find previously encountered items, this means one or more bins
    already exist for these items. If more than one bin exists we merge
    them (updating the reference of all contained items). Finally we put
    the current sequence's items in the bin.

    Usage:
    ::
        >>> result = merge_intersections([[1, 2], [2, 4], [7, 8], [3, 2], [4, 5]])
        >>> result = sorted(sorted(s) for s in result)
        [[1, 2, 3, 4, 5], [7, 8]]
    """
    bins: dict[T: set[T]] = dict()
    bin_refs: dict[T: T] = dict()
    for lst in lists:
        if not lst:
            continue

        # Gather the bin refs of all items in the list that we have
        # already seen.
        encountered_items_bin_refs = {
            bin_refs[item]
            for item in lst
            if item in bin_refs
        }
        if len(encountered_items_bin_refs) >= 1:
            # Some of the items in `lst` have already been seen in a
            # previous iteration. They are therefore already attached
            # to a bin. Select any of their corresponding bin ref.
            bin_ref = encountered_items_bin_refs.pop()
            # If the previously-seen items were not all attached to the
            # same bin, their respective bins need to be merged into
            # the selected one.
            if len(encountered_items_bin_refs) > 0:
                to_merge_bins = [bins.pop(ref) for ref in encountered_items_bin_refs]
                bins[bin_ref].update(chain(*to_merge_bins))
                for item in chain(*to_merge_bins):
                    bin_refs[item] = bin_ref
            bins[bin_ref].update(lst)
        else:
            # None of the items in `lst` have already been seen in a
            # previous iteration. Therefore, we can safely pick any
            # item as our new bin ref and create the corresponding bin.
            bin_ref = next(iter(lst))
            bins[bin_ref] = set(lst)
        for item in lst:
            bin_refs[item] = bin_ref
    return list(bins.values())

Результаты тестов:

      Timing with: >> Niklas << Benchmark
Info: 5000 lists, average size 305, max size 999
(from file: ./lists/timing_1.txt)
0.200 (1x) -- takeshi
0.328 (1.6x) -- alexis
0.473 (2.4x) -- agf
0.746 (3.7x) -- Rik. Poggi
0.776 (3.9x) -- Niks rewrite
0.792 (4x) -- Niklas B.
1.419 (7.1x) -- agf (optimized)
1.480 (7.4x) -- ChessMaster
1.579 (7.9x) -- katrielalex
1.627 (8.2x) -- steabert
1.938 (9.7x) -- robert king
9.273 (46x) -- Sven Marnach
33.779 (169x) -- hochl

Timing with: >> Niklas << Benchmark
Info: 4500 lists, average size 305, max size 999
(from file: ./lists/timing_2.txt)
0.158 (1x) -- takeshi
0.166 (1x) -- agf
0.231 (1.5x) -- Niks rewrite
0.232 (1.5x) -- Rik. Poggi
0.233 (1.5x) -- Niklas B.
0.268 (1.7x) -- alexis
0.408 (2.6x) -- ChessMaster
0.422 (2.7x) -- agf (optimized)
1.408 (8.9x) -- katrielalex
1.483 (9.4x) -- steabert
1.924 (12x) -- robert king
8.622 (55x) -- Sven Marnach
25.952 (164x) -- hochl

Timing with: >> Niklas << Benchmark
Info: 4500 lists, average size 98, max size 999
(from file: ./lists/timing_3.txt)
0.059 (1x) -- takeshi
0.068 (1.1x) -- agf
0.094 (1.6x) -- alexis
0.095 (1.6x) -- Rik. Poggi
0.095 (1.6x) -- Niklas B.
0.097 (1.6x) -- Niks rewrite
0.183 (3.1x) -- ChessMaster
0.192 (3.2x) -- agf (optimized)
0.425 (7.2x) -- katrielalex
0.586 (9.9x) -- robert king
0.787 (13x) -- steabert
2.827 (48x) -- Sven Marnach
9.162 (155x) -- hochl

Timing with: >> Sven << Benchmark
Info: 200 lists, average size 10, max size 10
0.000 (1x) -- alexis
0.001 (1.3x) -- ChessMaster
0.001 (1.8x) -- agf (optimized)
0.001 (1.9x) -- takeshi
0.002 (3.7x) -- steabert
0.002 (3.7x) -- robert king
0.002 (4.2x) -- katrielalex
0.002 (4.6x) -- Rik. Poggi
0.002 (4.8x) -- agf
0.002 (5.1x) -- Niklas B.
0.002 (5.5x) -- hochl
0.003 (6.1x) -- Niks rewrite
0.003 (7.7x) -- Sven Marnach

Timing with: >> Agf << Benchmark
Info: 2000 lists, average size 253, max size 500
0.030 (1x) -- Rik. Poggi
0.035 (1.2x) -- ChessMaster
0.036 (1.2x) -- agf
0.036 (1.2x) -- agf (optimized)
0.037 (1.2x) -- Niks rewrite
0.038 (1.3x) -- Niklas B.
0.060 (2x) -- hochl
0.074 (2.5x) -- takeshi
0.118 (3.9x) -- alexis
0.520 (17x) -- katrielalex
0.528 (18x) -- steabert
0.694 (23x) -- robert king
34.746 (1158x) -- Sven Marnach

Результаты теста:

      ### Going to test: takeshi ###

test_coverage (__main__.MergeTestCase)
Check coverage original data ... ok
test_disjoint (__main__.MergeTestCase)
Check disjoint-ness of merged results ... ok
test_subset (__main__.MergeTestCase)
Check that every original data is a subset ... ok

----------------------------------------------------------------------
Ran 3 tests in 0.008s

OK

Answer 16

Мое решение хорошо работает с небольшими списками и вполне читабельно без зависимостей.

def merge_list(starting_list):
    final_list = []
    for i,v in enumerate(starting_list[:-1]):
        if set(v)&set(starting_list[i+1]):
            starting_list[i+1].extend(list(set(v) - set(starting_list[i+1])))
        else:
            final_list.append(v)
    final_list.append(starting_list[-1])
    return final_list

Бенчмаркинг это:

списки = [[1,2,3], [3,5,6], [8,9,10], [11,12,13]]

% timeit merge_list (списки)

100000 циклов, лучшее из 3: 4,9 мкс на цикл

Answer 17

Это можно решить в O(n) с помощью алгоритма поиска объединения. Учитывая первые две строки ваших данных, ребрами для использования в объединении-поиске являются следующие пары: (0,1),(1,3),(1,0),(0,3),(3,4),(4,5),(5,10)

Answer 18

Использовать flag чтобы гарантировать получение окончательных взаимоисключающих результатов

def merge(lists): 
    while(1):
        flag=0
        for i in range(0,len(lists)):
            for j in range(i+1,len(lists)):
                if len(intersection(lists[i],lists[j]))!=0:
                    lists[i]=union(lists[i],lists[j])
                    lists.remove(lists[j])
                    flag+=1
                    break
        if flag==0:
            break
    return lists

Answer 19

from itertools import combinations


def merge(elements_list):
    d = {index: set(elements) for index, elements in enumerate(elements_list)}

    while any(not set.isdisjoint(d[i], d[j]) for i, j in combinations(d.keys(), 2)):
        merged = set()
        for i, j in combinations(d.keys(), 2):
            if not set.isdisjoint(d[i], d[j]):
                d[i] = set.union(d[i], d[j])
                merged.add(j)

        for k in merged:
            d.pop(k)    

    return [v for v in d.values() if v]

lst = [[65, 17, 5, 30, 79, 56, 48, 62],
       [6, 97, 32, 93, 55, 14, 70, 32],
       [75, 37, 83, 34, 9, 19, 14, 64],
       [43, 71],
       [],
       [89, 49, 1, 30, 28, 3, 63],
       [35, 21, 68, 94, 57, 94, 9, 3],
       [16],
       [29, 9, 97, 43],
       [17, 63, 24]]

print(merge(lst))