Учебник для scipy.cluster.hierarchy

Question

Я пытаюсь понять, как управлять иерархическим кластером, но документация слишком... техническая?... и я не могу понять, как это работает.

Есть ли какой-нибудь учебник, с которого можно начать, объясняя шаг за шагом некоторые простые задачи?

Допустим, у меня есть следующий набор данных:

a = np.array([[0,   0  ],
              [1,   0  ],
              [0,   1  ],
              [1,   1  ], 
              [0.5, 0  ],
              [0,   0.5],
              [0.5, 0.5],
              [2,   2  ],
              [2,   3  ],
              [3,   2  ],
              [3,   3  ]])

Я легко могу сделать иерархию кластеров и построить дендрограмму:

z = linkage(a)
d = dendrogram(z)

• Теперь, как я могу восстановить конкретный кластер? Допустим, тот, с элементами [0,1,2,4,5,6] в дендрограмме?
• Как я могу вернуть значения этих элементов?

Answer 1

Существует три этапа в иерархической агломерационной кластеризации (HAC):

1. Количественные данные (metric аргумент)
2. Данные кластера (method аргумент)
3. Выберите количество кластеров

дела

z = linkage(a)

выполнит первые два шага. Поскольку вы не указали никаких параметров, он использует стандартные значения

1. metric = 'euclidean'
2. method = 'single'

Так z = linkage(a) даст вам единую связанную иерархическую агломерацию a, Эта кластеризация является своего рода иерархией решений. Из этой иерархии вы получаете некоторую информацию о структуре ваших данных. Что вы можете сделать сейчас:

• Проверьте, какие metric уместно, например cityblock или же chebychev будет количественно определять ваши данные (cityblock, euclidean а также chebychev соответствовать L1, L2, а также L_inf норма)
• Проверьте различные свойства / поведение methdos (например single, complete а также average)
• Проверьте, как определить количество кластеров, например, читая вики об этом
• Вычислить индексы для найденных решений (кластеров), таких как коэффициент силуэта (с этим коэффициентом вы получаете обратную связь о качестве того, насколько хорошо точка / наблюдение соответствует кластеру, которому она назначена кластеризацией). Различные индексы используют разные критерии для определения кластеризации.

Вот с чего начать

import numpy as np
import scipy.cluster.hierarchy as hac
import matplotlib.pyplot as plt


a = np.array([[0.1,   2.5],
              [1.5,   .4 ],
              [0.3,   1  ],
              [1  ,   .8 ],
              [0.5,   0  ],
              [0  ,   0.5],
              [0.5,   0.5],
              [2.7,   2  ],
              [2.2,   3.1],
              [3  ,   2  ],
              [3.2,   1.3]])

fig, axes23 = plt.subplots(2, 3)

for method, axes in zip(['single', 'complete'], axes23):
    z = hac.linkage(a, method=method)

    # Plotting
    axes[0].plot(range(1, len(z)+1), z[::-1, 2])
    knee = np.diff(z[::-1, 2], 2)
    axes[0].plot(range(2, len(z)), knee)

    num_clust1 = knee.argmax() + 2
    knee[knee.argmax()] = 0
    num_clust2 = knee.argmax() + 2

    axes[0].text(num_clust1, z[::-1, 2][num_clust1-1], 'possible\n<- knee point')

    part1 = hac.fcluster(z, num_clust1, 'maxclust')
    part2 = hac.fcluster(z, num_clust2, 'maxclust')

    clr = ['#2200CC' ,'#D9007E' ,'#FF6600' ,'#FFCC00' ,'#ACE600' ,'#0099CC' ,
    '#8900CC' ,'#FF0000' ,'#FF9900' ,'#FFFF00' ,'#00CC01' ,'#0055CC']

    for part, ax in zip([part1, part2], axes[1:]):
        for cluster in set(part):
            ax.scatter(a[part == cluster, 0], a[part == cluster, 1], 
                       color=clr[cluster])

    m = '\n(method: {})'.format(method)
    plt.setp(axes[0], title='Screeplot{}'.format(m), xlabel='partition',
             ylabel='{}\ncluster distance'.format(m))
    plt.setp(axes[1], title='{} Clusters'.format(num_clust1))
    plt.setp(axes[2], title='{} Clusters'.format(num_clust2))

plt.tight_layout()
plt.show()

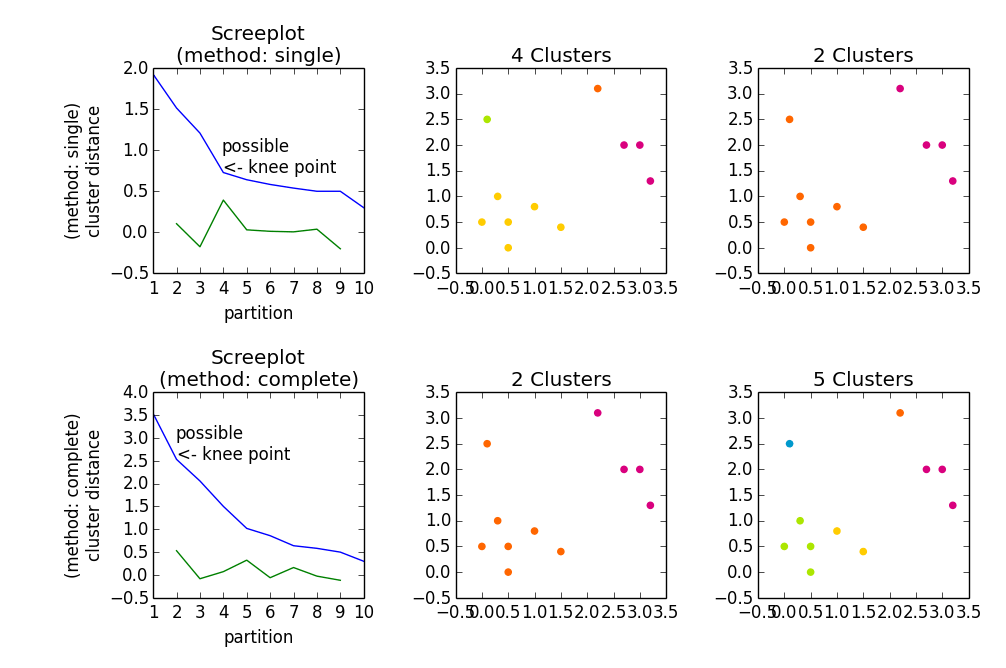
дает