Симуляция ошибок типа I в R

Question

Я пытаюсь рассчитать частоту ошибок и мощность типа i для корреляционного теста для двумерных нормальных данных с использованием моделирования Монте-Карло.

Но я получаю неожиданные значения для ошибки типа I и мощности. (ошибка типа I как 0,864)

Мне нужно знать, сделал ли я какую-то ошибку. Может кто-нибудь мне помочь?

set.seed(160230)
library("mvtnorm", lib.loc="~/R/win-library/3.4")
sigma= matrix(c(1,0.8,0.8,1),2,2) 
mu <- c(0,0)
#bivariate normal data
sim=replicate(n=1000 , rmvnorm(10,mean=mu , sigma = sigma))

pval1=c()

for(i in 1:1000)
{
 pval1[i]=cor.test(sim[,1,i],sim[,2,i],method = c("pearson"))$p.value

  }
#type1 error rate
mean(pval1<0.05)

#power
mean(pval3>0.05)

Answer 1

Ваш код в порядке, но вы неправильно настроили симуляции.

В вашем коде вы

1. Смоделируйте двумерные данные с сильной корреляцией, rho=0,8.
2. Проверьте гипотезу, что H0: rho=0.

Таким образом, вы моделируете данные в соответствии с альтернативной гипотезой, поэтому вы получаете результат 0,864. Это по сути ваша сила для этой конкретной альтернативы. Вместо этого вы можете сделать следующее:

Сначала смоделируйте данные под нулевой гипотезой

sigma <- matrix(c(1,0,0,1),2,2) 
mu <- c(0,0)
#bivariate normal data under H0
sim <- replicate(n=1000, rmvnorm(10, mean=mu, sigma = sigma))

# Test the actual level under H0

result <- sapply(1:1000, function(i) { 
    cor.test(sim[,1,i],sim[,2,i],method = c("pearson"))$p.value})

mean(result < 0.05)

что дает значение около 0,05. По альтернативе вы можете использовать свой код с соотношением 0,8 (или каким-либо другим числом). Вы можете обобщить это с помощью следующего кода, чтобы легко получить мощность для нескольких корреляций.

rho <- seq(0, .9, .1)
pwr <- sapply(rho, function(r) {
    sigma <- matrix(c(1,r,r,1),2,2) 
    mu <- c(0,0)
    #bivariate normal data 
    sim <- replicate(n=1000, rmvnorm(10, mean=mu, sigma = sigma))

    # Test the actual level
    result <- sapply(1:1000, function(i) { 
        cor.test(sim[,1,i],sim[,2,i],method = c("pearson"))$p.value})

    mean(result < 0.05)
})

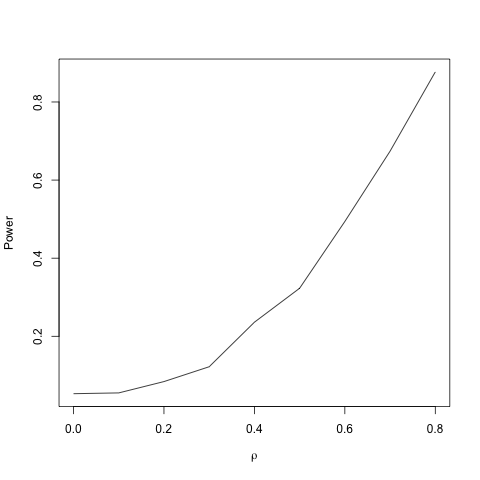
Затем вы можете увидеть влияние корреляции на мощность, отображая отношения

plot(rho, pwr, type="l", xlab=expression(rho), ylab="Power")