Алгоритм Fast Arc Cos?
У меня есть своя, очень быстрая функция cos:
float sine(float x)
{
const float B = 4/pi;
const float C = -4/(pi*pi);
float y = B * x + C * x * abs(x);
// const float Q = 0.775;
const float P = 0.225;
y = P * (y * abs(y) - y) + y; // Q * y + P * y * abs(y)
return y;
}
float cosine(float x)
{
return sine(x + (pi / 2));
}
Но теперь, когда я создаю профиль, я вижу, что acos() убивает процессор. Мне не нужна интенсивная точность. Какой быстрый способ рассчитать acos(x) Спасибо.
8 ответов
Простое кубическое приближение, полином Лагранжа для x ∈ {-1, -½, 0, ½, 1}, имеет вид:
double acos(x) {
return (-0.69813170079773212 * x * x - 0.87266462599716477) * x + 1.5707963267948966;
}
Максимальная погрешность составляет около 0,18 рад.
Есть запасная память? Таблица поиска (с интерполяцией, если требуется) будет самой быстрой.
У nVidia есть несколько замечательных ресурсов, которые показывают, как аппроксимировать очень дорогие математические функции, например: acos asin atan2 и т. д.
Эти алгоритмы дают хорошие результаты, когда скорость выполнения более важна (в пределах разумного), чем точность. Вот их функция acos:
// Absolute error <= 6.7e-5
float acos(float x) {
float negate = float(x < 0);
x = abs(x);
float ret = -0.0187293;
ret = ret * x;
ret = ret + 0.0742610;
ret = ret * x;
ret = ret - 0.2121144;
ret = ret * x;
ret = ret + 1.5707288;
ret = ret * sqrt(1.0-x);
ret = ret - 2 * negate * ret;
return negate * 3.14159265358979 + ret;
}
А вот результаты для расчета acos(0.5):
nVidia: result: 1.0471513828611643
math.h: result: 1.0471975511965976
Это довольно близко! В зависимости от требуемой степени точности, это может быть хорошим вариантом для вас.
У меня есть свой. Это довольно точно и вроде быстро. Он работает на основе теоремы, которую я построил вокруг сходимости четвертого порядка. Это действительно интересно, и вы можете увидеть уравнение и то, как быстро оно может приблизить мое естественное логарифмическое приближение здесь: https://www.desmos.com/calculator/yb04qt8jx4
Вот мой код arccos:
function acos(x)
local a=1.43+0.59*x a=(a+(2+2*x)/a)/2
local b=1.65-1.41*x b=(b+(2-2*x)/b)/2
local c=0.88-0.77*x c=(c+(2-a)/c)/2
return (8*(c+(2-a)/c)-(b+(2-2*x)/b))/6
end
Многое из этого - просто приближение квадратного корня. Он также работает очень хорошо, если только вы не слишком близко к получению квадратного корня из 0. Он имеет среднюю ошибку (исключая x=0,99 к 1) 0,0003. Проблема, однако, в том, что при 0,99 он начинает дерьмо, а при х =1 разница в точности становится 0,05. Конечно, это можно решить, выполнив больше итераций с квадратными корнями (lol nope) или, если немного, например, если x>0.99, то использовать другой набор линеаризаций квадратного корня, но это делает код длинным и уродливым.,
Если вам не очень важна точность, вы можете просто сделать одну итерацию на квадратный корень, что все равно должно держать вас где-то в диапазоне 0,0162 или что-то еще, насколько это возможно:
function acos(x)
local a=1.43+0.59*x a=(a+(2+2*x)/a)/2
local b=1.65-1.41*x b=(b+(2-2*x)/b)/2
local c=0.88-0.77*x c=(c+(2-a)/c)/2
return 8/3*c-b/3
end
Если вы согласны с этим, вы можете использовать уже существующий код с квадратным корнем. Это избавит от уравнения, которое сходит с ума при x=1:
function acos(x)
local a = math.sqrt(2+2*x)
local b = math.sqrt(2-2*x)
local c = math.sqrt(2-a)
return 8/3*d-b/3
end
Честно говоря, хотя, если вам действительно не хватает времени, помните, что вы можете линеаризовать arccos в 3.14159-1.57079x и просто сделать:
function acos(x)
return 1.57079-1.57079*x
end
В любом случае, если вы хотите увидеть список моих уравнений аппроксимации арккос, вы можете перейти по https://www.desmos.com/calculator/tcaty2sv8l Я знаю, что мои аппроксимации не являются лучшими для некоторых вещей, но если вы Вы делаете что-то, где мои приближения будут полезны, пожалуйста, используйте их, но попробуйте дать мне кредит.
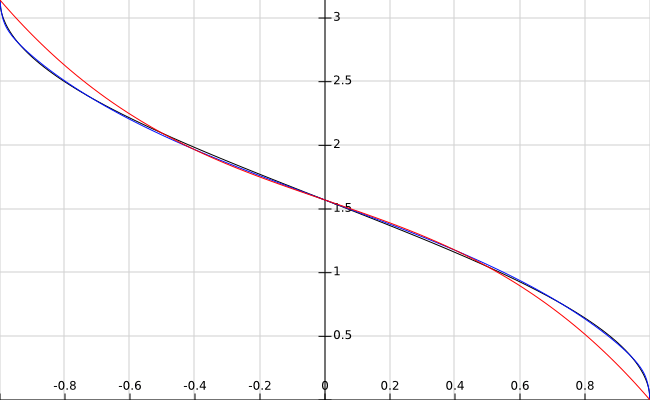
Вы можете аппроксимировать обратный косинус с помощью полинома, как предложено dan04, но полином - довольно плохое приближение вблизи -1 и 1, где производная обратного косинуса уходит в бесконечность. Когда вы увеличиваете степень многочлена, вы нажимаете на убывающую отдачу быстро, и все еще трудно получить хорошее приближение к конечным точкам. Рациональная функция (отношение двух полиномов) может дать гораздо лучшее приближение в этом случае.
acos(x) ≈ π/2 + (ax + bx³) / (1 + cx² + dx⁴)
где
a = -0.939115566365855
b = 0.9217841528914573
c = -1.2845906244690837
d = 0.295624144969963174
имеет максимальную абсолютную погрешность 0,017 радиан (0,96 градуса) на интервале (-1, 1). Вот график (обратный косинус в черном, приближение кубического полинома в красном, функция выше в синем) для сравнения:
Вышеприведенные коэффициенты были выбраны, чтобы минимизировать максимальную абсолютную ошибку во всей области. Если вы хотите допустить большую ошибку на конечных точках, ошибку на интервале (-0,98, 0,98) можно сделать намного меньшей. Числитель степени 5 и знаменатель степени 2 примерно такой же быстрый, как указанная выше функция, но немного менее точен. За счет производительности вы можете повысить точность, используя полиномы более высокой степени.
Замечание о производительности: вычисление двух полиномов по-прежнему очень дешево, и вы можете использовать объединенные инструкции умножения-сложения. Деление не так уж плохо, потому что вы можете использовать аппаратное взаимное приближение и умножение. Ошибка в обратном приближении незначительна по сравнению с ошибкой в приближении acos. На 2,6 ГГц Skylake i7 это приближение может делать около 8 обратных косинусов каждые 6 циклов с использованием AVX. (То есть пропускная способность, задержка превышает 6 циклов.)
Другой подход, который вы можете использовать, это использовать комплексные числа. Из формулы де Мойвра
ⅈx = cos (π / 2 * x) + ⅈ * sin (π / 2 * x)
Пусть θ = π/2*x. Тогда x = 2θ/π, поэтому
- грех (θ) = ℑ (ⅈ ^2θ / π)
- cos (θ) = ℜ (ⅈ ^2θ / π)
Как вы можете рассчитать силы ⅈ без греха и cos? Начните с предварительно вычисленной таблицы для степеней 2:
- ⅈ4 = 1
- ⅈ2 = -1
- ⅈ1 = ⅈ
- ⅈ1/2 = 0,7071067811865476 + 0,7071067811865475 * ⅈ
- ⅈ1/4 = 0,9238795325112867 + 0,3826834323650898 * ⅈ
- ⅈ1/8 = 0,9807852804032304 + 0,19509032201612825 * ⅈ
- 1/16 = 0,9951847266721969 + 0,0980171403295606 * *
- ⅈ1/32 = 0,9995954562051724 + 0,049067674327418015 * ⅈ
- ⅈ1/64 = 0,9996988186962042 + 0,024541228522912288 * ⅈ
- ⅈ1/128 = 0,999997018391445 + 0,012271538285719925 * ⅈ
- 251/256 = 0,9999911752826011 + 0,006135884649154475 * ⅈ
Чтобы вычислить произвольные значения ⅈx, аппроксимируйте показатель степени в виде двоичной дроби, а затем умножьте вместе соответствующие значения из таблицы.
Например, чтобы найти грех и cos 72 ° = 0,8π / 2:
ⅈ0,8≈ 25205/256= ⅈ0b11001101= ⅈ1/2 * ⅈ1/4 * ⅈ1/32 * ⅈ1/64 * ⅈ1/256
= 0,3078496400415349 + 0,9514350209690084 * ⅈ
- грех (72°) ≈ 0,9514350209690084 ("точное" значение 0,9510565162951535)
- cos (72°) ≈ 0,3078496400415349 ("точное" значение - 0,30901699437494745).
Чтобы найти asin и acos, вы можете использовать эту таблицу с методом деления пополам:
Например, чтобы найти asin(0,6) (наименьший угол в треугольнике 3-4-5):
- ⅈ0 = 1 + 0* ⅈ. Грех слишком мал, поэтому увеличьте х на 1/2.
- ⅈ1/2 = 0,7071067811865476 + 0,7071067811865475* ⅈ. Грех слишком велик, поэтому уменьшите х на 1/4.
- ⅈ1/4 = 0,9238795325112867 + 0,3826834323650898* ⅈ. Грех слишком мал, поэтому увеличьте х на 1/8.
- ⅈ3/8 = 0,8314696123025452 + 0,5555702330196022* ⅈ. Грех все еще слишком мал, поэтому увеличьте х на 1/16.
- ⅈ7/16 = 0,773010453362737 + 0,6343932841636455* ⅈ. Грех слишком велик, поэтому уменьшите х на 1/32.
- /13/32 = 0,8032075314806449 + 0,5956993044924334* ⅈ.
Каждый раз, когда вы увеличиваете x, умножьте на соответствующую степень ⅈ. Каждый раз, когда вы уменьшаете x, делите на соответствующую степень ⅈ.
Если мы остановимся здесь, мы получим acos(0,6) ≈ 13/32*π/2 = 0,6381360077604268 ("точное" значение составляет 0,6435011087932844.)
Точность, конечно, зависит от количества итераций. Для быстрого и грязного приближения используйте 10 итераций. Для "высокой точности" используйте 50-60 итераций.
Быстрая реализация арккозина с точностью около 0,5 градуса может быть основана на наблюдении, что для x в [0,1], acos(x) ≈ √(2*(1-x)). Дополнительный масштабный коэффициент повышает точность около нуля. Оптимальный фактор может быть найден простым бинарным поиском. Отрицательные аргументы обрабатываются в соответствии с acos (-x) = π - acos (x).
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <string.h>
#include <math.h>
// Approximate acos(a) with relative error < 5.15e-3
// This uses an idea from Robert Harley's posting in comp.arch.arithmetic on 1996/07/12
// https://groups.google.com/forum/#!original/comp.arch.arithmetic/wqCPkCCXqWs/T9qCkHtGE2YJ
float fast_acos (float a)
{
const float PI = 3.14159265f;
const float C = 0.10501094f;
float r, s, t, u;
t = (a < 0) ? (-a) : a; // handle negative arguments
u = 1.0f - t;
s = sqrtf (u + u);
r = C * u * s + s; // or fmaf (C * u, s, s) if FMA support in hardware
if (a < 0) r = PI - r; // handle negative arguments
return r;
}
float uint_as_float (uint32_t a)
{
float r;
memcpy (&r, &a, sizeof(r));
return r;
}
int main (void)
{
double maxrelerr = 0.0;
uint32_t a = 0;
do {
float x = uint_as_float (a);
float r = fast_acos (x);
double xx = (double)x;
double res = (double)r;
double ref = acos (xx);
double relerr = (res - ref) / ref;
if (fabs (relerr) > maxrelerr) {
maxrelerr = fabs (relerr);
printf ("xx=% 15.8e res=% 15.8e ref=% 15.8e rel.err=% 15.8e\n",
xx, res, ref, relerr);
}
a++;
} while (a);
printf ("maximum relative error = %15.8e\n", maxrelerr);
return EXIT_SUCCESS;
}
Выходные данные вышеупомянутого тестового леса должны выглядеть примерно так:
xx= 0.00000000e+000 res= 1.56272149e+000 ref= 1.57079633e+000 rel.err=-5.14060021e-003
xx= 2.98023259e-008 res= 1.56272137e+000 ref= 1.57079630e+000 rel.err=-5.14065723e-003
xx= 8.94069672e-008 res= 1.56272125e+000 ref= 1.57079624e+000 rel.err=-5.14069537e-003
xx=-2.98023259e-008 res= 1.57887137e+000 ref= 1.57079636e+000 rel.err= 5.14071269e-003
xx=-8.94069672e-008 res= 1.57887149e+000 ref= 1.57079642e+000 rel.err= 5.14075044e-003
maximum relative error = 5.14075044e-003
Вот отличный веб-сайт с множеством вариантов: https://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/arcsin/onlyelem.html
Лично я пошел с приближением Чебышева-Паде со следующим кодом:
double arccos(double x) {
const double pi = 3.141592653;
return pi / 2 - (.5689111419 - .2644381021*x - .4212611542*(2*x - 1)*(2*x - 1)
+ .1475622352*(2*x - 1)*(2*x - 1)*(2*x - 1))
/ (2.006022274 - 2.343685222*x + .3316406750*(2*x - 1)*(2*x - 1) +
.02607135626*(2*x - 1)*(2*x - 1)*(2*x - 1));
}
Если вы используете Microsoft VC++, вот версия встроенного кода FPU __asm x87 без всех заполнителей CRT, проверок ошибок и т. Д., И в отличие от самого раннего классического кода ASM, который вы можете найти, он использует FMUL вместо более медленного FDIV. Он компилируется / работает с Microsoft VC++ 2005 Express/Pro, чего я всегда придерживаюсь по разным причинам.
Немного сложно настроить функцию с помощью "__declspec(naked)/__fastcall", правильно извлекать параметры, обрабатывать стек, так что не для слабонервных. Если он не компилируется с ошибками в вашей версии, не беспокойтесь, если у вас нет опыта. Или спросите меня, я могу переписать его в более дружелюбном блоке __asm {}. Я бы вручную встроил это, если это критическая часть функции в цикле для дальнейшего повышения производительности, если это необходимо.
extern float __fastcall fs_acos(float x);
extern double __fastcall fs_Acos(double x);
// ACOS(x)- Computes the arccosine of ST(0)
// Allowable range: -1<=x<=+1
// Derivative Formulas: acos(x) = atan(sqrt((1 - x * x)/(x * x))) OR
// acos(x) = atan2(sqrt(1 - x * x), x)
// e.g. acos(-1.0) = 3.1415927
__declspec(naked) float __fastcall fs_acos(float x) { __asm {
FLD DWORD PTR [ESP+4] ;// Load/Push parameter 'x' to FPU stack
FLD1 ;// Load 1.0
FADD ST, ST(1) ;// Compute 1.0 + 'x'
FLD1 ;// Load 1.0
FSUB ST, ST(2) ;// Compute 1.0 - 'x'
FMULP ST(1), ST ;// Compute (1-x) * (1+x)
FSQRT ;// Compute sqrt(result)
FXCH ST(1)
FPATAN ;// Compute arctangent of result / 'x' (ST1/ST0)
RET 4
}}
__declspec(naked) double __fastcall fs_Acos(double x) { __asm { //
FLD QWORD PTR [ESP+4] ;// Load/Push parameter 'x' to FPU stack
FLD1 ;// Load 1.0
FADD ST, ST(1) ;// Compute (1.0 + 'x')
FLD1 ;// Load 1.0
FSUB ST, ST(2) ;// Compute (1.0 - 'x')
FMULP ST(1), ST ;// Compute (1-x) * (1+x)
FSQRT ;// Compute sqrt((1-x) * (1+x))
FXCH ST(1)
FPATAN ;// Compute arctangent of result / 'x' (ST1/ST0)
RET 8
}}
К сожалению, у меня недостаточно репутации для комментариев. Вот небольшая модификация функции Nvidia, которая касается того факта, что числа, которые должны быть <= 1, при максимально сохранении производительности.
Это может быть важно, поскольку ошибки округления могут привести к тому, что число, которое должно быть 1,0, будет (ну, немного) больше 1,0.
double safer_acos(double x) {
double negate = double(x < 0);
x = abs(x);
x -= double(x>1.0)*(x-1.0); // <- equivalent to min(1.0,x), but faster
double ret = -0.0187293;
ret = ret * x;
ret = ret + 0.0742610;
ret = ret * x;
ret = ret - 0.2121144;
ret = ret * x;
ret = ret + 1.5707288;
ret = ret * sqrt(1.0-x);
ret = ret - 2 * negate * ret;
return negate * 3.14159265358979 + ret;
// In a single line (no gain using gcc)
//return negate * 3.14159265358979 + (((((-0.0187293*x)+ 0.0742610)*x - 0.2121144)*x + 1.5707288)* sqrt(1.0-x))*(1.0-2.0*negate);
}
float v,x;
cin>>x;
v=x;
x=(x*3.141592654)/180;
float a,b,c,d,e,f,g,sum=0;
a=(x*x)/ar[2];
b=(x*x*x*x)/ar[4];
c=(x*x*x*x*x*x)/ar[6];
d=(x*x*x*x*x*x*x*x)/ar[8];
sum=1-a+b-c+d;
cout<<"cos("<<v<<") = "<<sum;