Положение солнца с учетом времени суток, широты и долготы в php

Question

Это php-реализация кода Джоша r для вычисления положения солнца для данной даты и времени:

Это исправленный код после помощи MvG:

function getSunPosition($lat, $long, $year, $month, $day, $hour, $min) {
  // From https://stackru.com/questions/8708048/position-of-the-sun-given-time-of-day-latitude-and-longitude?rq=1

  // Get Julian date for date at noon
  $jd = gregoriantojd($month,$day,$year);

  //correct for half-day offset
  $dayfrac = $hour / 24 - .5;

  //now set the fraction of a day      
  $frac = $dayfrac + $min / 60 / 24;
  $jd = $jd + $frac;

  // The input to the Atronomer's almanach is the difference between
  // the Julian date and JD 2451545.0 (noon, 1 January 2000)
  $time = ($jd - 2451545);
  // Ecliptic coordinates

  // Mean longitude
  $mnlong = (280.460 + 0.9856474 * $time);
  $mnlong = fmod($mnlong,360);      
  if ($mnlong < 0) $mnlong = ($mnlong + 360);

  // Mean anomaly
  $mnanom = (357.528 + 0.9856003 * $time);
  $mnanom = fmod($mnanom,360);
  if ($mnanom < 0) $mnanom = ($mnanom + 360);
  $mnanom = deg2rad($mnanom);

  // Ecliptic longitude and obliquity of ecliptic
  $eclong = ($mnlong + 1.915 * sin($mnanom) + 0.020 * sin(2 * $mnanom));
  $eclong = fmod($eclong,360);
  if ($eclong < 0) $eclong = ($eclong + 360);
  $oblqec = (23.439 - 0.0000004 * $time);
  $eclong = deg2rad($eclong);
  $oblqec = deg2rad($oblqec);

  // Celestial coordinates
  // Right ascension and declination
  $num = (cos($oblqec) * sin($eclong));
  $den = (cos($eclong));
  $ra = (atan($num / $den));
  if ($den < 0) $ra = ($ra + pi());
  if ($den >= 0 && $num <0) $ra = ($ra + 2*pi());
  $dec = (asin(sin($oblqec) * sin($eclong)));

  // Local coordinates
  // Greenwich mean sidereal time
  //$h = $hour + $min / 60 + $sec / 3600;
  $h = $hour + $min / 60;
  $gmst = (6.697375 + .0657098242 * $time + $h);
  $gmst = fmod($gmst,24);
  if ($gmst < 0) $gmst = ($gmst + 24);

  // Local mean sidereal time
  $lmst = ($gmst + $long / 15);
  $lmst = fmod($lmst,24);
  if ($lmst < 0) $lmst = ($lmst + 24);
  $lmst = deg2rad($lmst * 15);

  // Hour angle
  $ha = ($lmst - $ra);
  if ($ha < pi()) $ha = ($ha + 2*pi());
  if ($ha > pi()) $ha = ($ha - 2*pi());

  // Latitude to radians
  $lat = deg2rad($lat);

  // Azimuth and elevation
  $el = (asin(sin($dec) * sin($lat) + cos($dec) * cos($lat) * cos($ha)));
  $az = (asin(-cos($dec) * sin($ha) / cos($el)));

  // For logic and names, see Spencer, J.W. 1989. Solar Energy. 42(4):353      
  if ((sin($dec) - sin($el) * sin($lat)) >00) {
    if(sin($az) < 0) $az = ($az + 2*pi());
  } else {
    $az = (pi() - $az);
  }

  $el = rad2deg($el);
  $az = rad2deg($az);
  $lat = rad2deg($lat);

  return array(number_format($el,2),number_format($az,2));
}

Это было проверено с Конго (около Экватора) широта / долгота: -4,77867 / 11,86364 на дату 1 сентября 2013 года в 10:00. В этом случае правильный ответ: высота = 67,77503 азимута = 54,51532

Спасибо за вашу помощь в отладке этого PHP-кода!

Грег Фабр.

Answer 1

Я верю линии

if ($dayfrac < 0) $dayfrac += 1;

в ошибке. Если вы находитесь до полудня, вы не хотите ссылаться на то же время днем ​​позже, но вместо этого вы хотите указать время до полудня, то есть вычесть из юлианской даты, которая представляет полдень.

При удалении этой строки примерная дата соответствует дате, вычисленной с использованием http://www.imcce.fr/en/grandpublic/temps/jour_julien.php, а именно 2456536.9166666665. Результирующий

$el = 67.775028608168
$az = 54.515316112281

Выглядит довольно хорошо для меня. В частности, это согласуется с пробегом R

elevation = 67.77503
azimuth = 54.51532

а также с тем, что говорит Stellarium (хотя я цитировал это неправильно в комментарии выше):

Alt = 67°46'30" = 67.775
Az  = 54°30'60" = 45.5167

Он также (почти) согласен с http://www.sunearthtools.com/, поэтому, я полагаю, вы допустили ошибку при первом вводе данных:

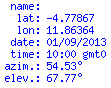
Так что я бы сказал, что это решает проблему.