Пространственная статистика с несколькими выходами и гауссовскими процессами

Question

В последнее время я изучаю гауссовские процессы. Перспектива вероятностного мульти-вывода является многообещающей в моей области. В частности, пространственная статистика. Но я столкнулся с тремя проблемами:

1. мульти-Ouput
2. переоснащение и
3. анизотропии.

Позвольте мне провести простое тематическое исследование с meuse набор данных (из пакета R sp).

ОБНОВЛЕНИЕ: Блокнот Jupyter, используемый для этого вопроса и обновленный в соответствии с ответом Грра, находится здесь.

import pandas as pd
import numpy as np
import matplotlib.pylab as plt
%matplotlib inline

meuse = pd.read_csv(filepath_or_buffer='https://gist.githubusercontent.com/essicolo/91a2666f7c5972a91bca763daecdc5ff/raw/056bda04114d55b793469b2ab0097ec01a6d66c6/meuse.csv', sep=',')

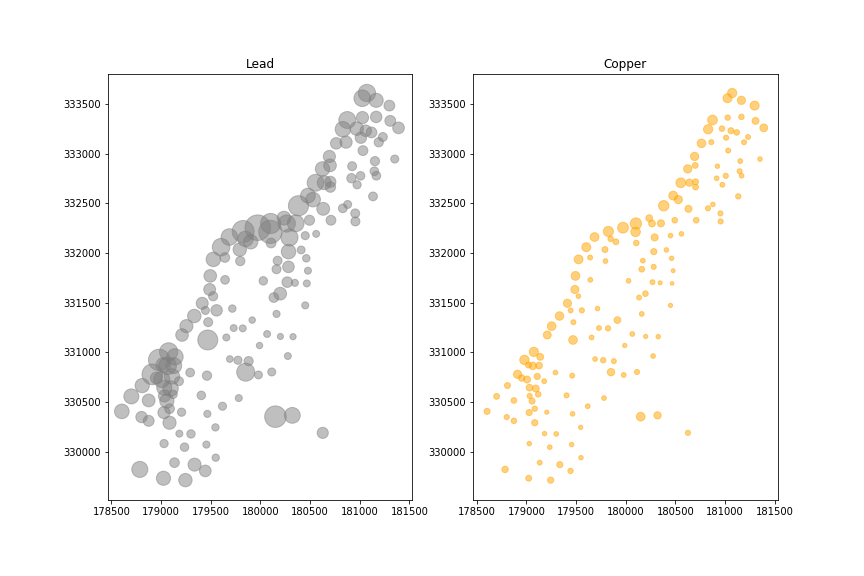
Для примера остановимся на меди и свинце.

fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(121, aspect=1)
ax1.set_title('Lead')
ax1.scatter(x=meuse.x, y=meuse.y, s=meuse.lead, alpha=0.5, color='grey')

ax2 = fig.add_subplot(122, aspect=1)
ax2.set_title('Copper')
ax2.scatter(x=meuse.x, y=meuse.y, s=meuse.copper, alpha=0.5, color='orange')

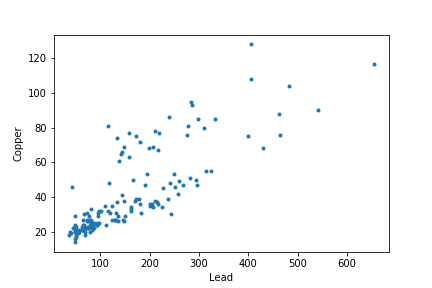
На самом деле, концентрации меди и свинца взаимосвязаны.

plt.plot(meuse['lead'], meuse['copper'], '.')
plt.xlabel('Lead')
plt.ylabel('Copper')

Таким образом, это проблема с несколькими выходами.

from sklearn.gaussian_process.kernels import RBF
from sklearn.gaussian_process import GaussianProcessRegressor as GPR
reg = GPR(kernel=RBF())
reg.fit(X=meuse[['x', 'y']], y=meuse[['lead', 'copper']])
predicted = reg.predict(meuse[['x', 'y']])

Первый вопрос: построено ли ядро ​​для коррелированного мульти-вывода, когда у имеет более одного измерения? Если нет, как я могу указать ядро?

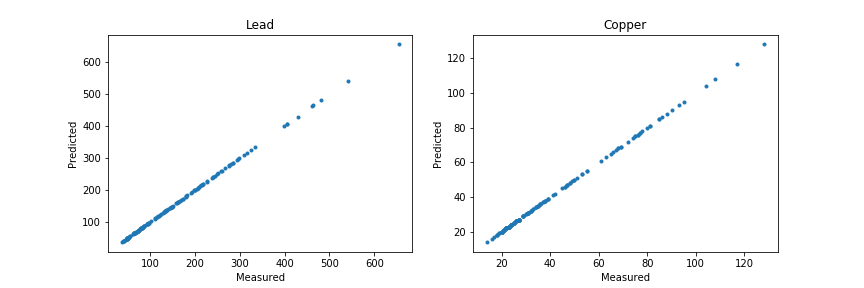
Я продолжаю анализ, чтобы показать вторую проблему, переоснащение:

fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(121)
ax1.set_title('Lead')
ax1.set_xlabel('Measured')
ax1.set_ylabel('Predicted')
ax1.plot(meuse.lead, predicted[:,0], '.')

ax2 = fig.add_subplot(122)
ax2.set_title('Copper')
ax2.set_xlabel('Measured')
ax2.set_ylabel('Predicted')
ax2.plot(meuse.copper, predicted[:,1], '.')

Я создал сетку координат х и у, и все концентрации в этой сетке были предсказаны как нули.

Наконец, последняя проблема, которая особенно проявляется в 3D для почв: как я могу указать анизотропию в таких моделях?

Answer 1

Прежде всего вам нужно разделить ваши данные. Обучение модели, а затем прогнозирование на тех же данных обучения будет выглядеть как переобучение, как вы наблюдали, но вы не тестировали свою модель на каких-либо удерживающих данных, поэтому вы не представляете, как она работает в дикой природе. Попробуйте разделить ваши данные с sklearn.model_selection.train_test_split вот так:

X_train, X_test, y_train, y_test = train_test_split(meuse[['x', 'y']], meuse[['lead', 'copper']])

Тогда вы можете тренировать свою модель. Тем не менее, у вас также есть проблема там. Когда вы тренируете модель так, как вы это делаете, вы получаете ядро ​​с length_scale=1e-05, По сути, в вашей модели нет шума. Прогнозы, сделанные с помощью этой настройки, будут так сильно центрированы вокруг ваших входных точек (X_train) что вы не сможете делать какие-либо прогнозы относительно сайтов вокруг них. Вам нужно изменить alpha параметр GaussianProcessRegressor чтобы исправить это. Это то, что вам, вероятно, понадобится для поиска по сетке, поскольку значение по умолчанию 1e-10. Для примера я использовал alpha=0.1,

reg = GPR(RBF(), alpha=0.1)
reg.fit(X_train, y_train)
predicted = reg.predict(X_test)

fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(121)
ax1.set_title('Lead')
ax1.set_xlabel('Measured')
ax1.set_ylabel('Predicted')
ax1.plot(y_test.lead, predicted[:,0], '.')

ax2 = fig.add_subplot(122)
ax2.set_title('Copper')
ax2.set_xlabel('Measured')
ax2.set_ylabel('Predicted')
ax2.plot(y_test.copper, predicted[:,1], '.')

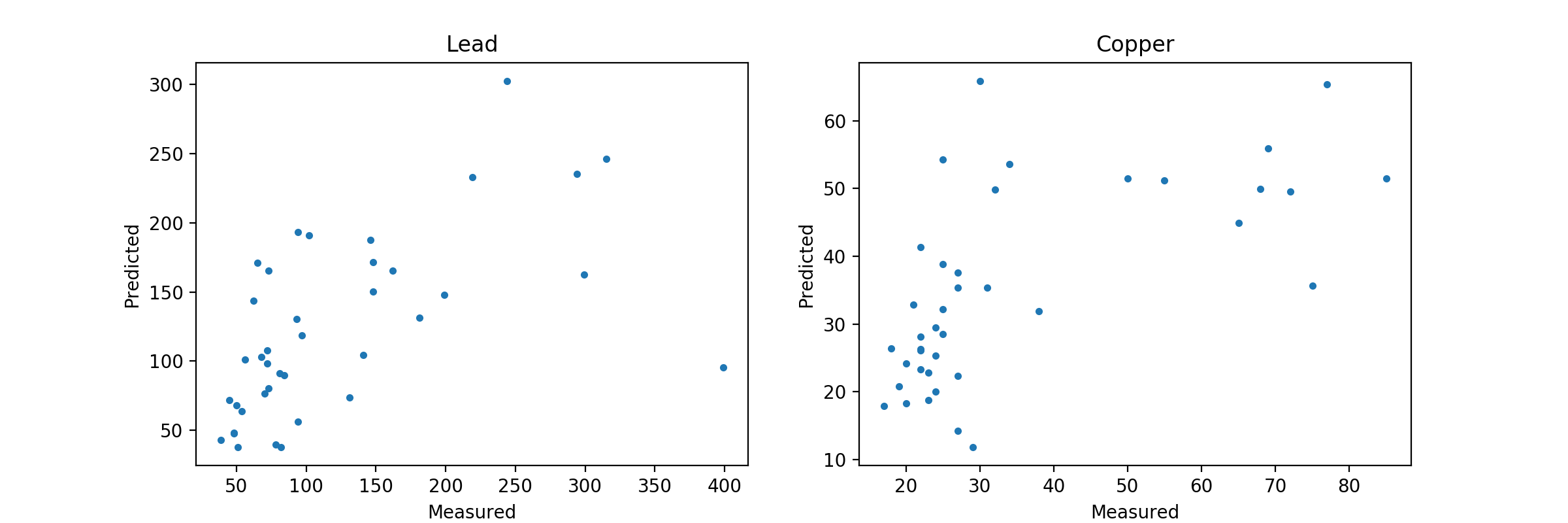
Это приводит к этому графику:

Как вы можете видеть, здесь нет проблем с переоснащением, на самом деле это может быть недостаточно. Как я уже говорил, вам нужно будет сделать несколько GridSearchCV для этой модели, чтобы создать оптимальную настройку с учетом ваших данных.

Итак, чтобы ответить на ваши вопросы:

1. Модель отлично справляется с мульти выходом.

2. Устранение неисправностей может быть решено путем правильного разделения данных или тестирования на другом наборе задержек.

3. Взгляните на раздел " Ядро радиальной базисной функции RBF " руководства по гауссовским процессам, чтобы узнать, как применять анизотропное ядро ​​в отличие от применяемого выше изотропного ядра.

Обновление вопроса в комментариях

Когда вы пишете "модель обрабатывает несколько выходов достаточно хорошо, как есть", вы говорите, что модель "как есть" построена для коррелированных целей, или что модель обрабатывает их достаточно хорошо, как набор независимых моделей?

Хороший вопрос. Из того, что я понимаю о GaussianProcessRegressor, я не верю, что он способен хранить несколько моделей внутри. Так что это единственная модель. При этом, что интересно в вашем вопросе, так это утверждение "построено для взаимосвязанных целей". В этой ситуации наши две цели действительно кажутся достаточно коррелированными (коэффициент корреляции Пирсона = 0,818, р =1,25e-38), поэтому я действительно вижу здесь два вопроса:

1. Для коррелированных данных, если мы построим модели для обеих целей, а также для отдельных целей, как будут сравниваться результаты?

2. Для некоррелированных данных справедливо ли сказанное выше?

К сожалению, мы не можем проверить второй вопрос, не создав новый "поддельный" набор данных, который несколько выходит за рамки того, что мы здесь делаем. Мы можем, однако, ответить на первый вопрос довольно легко. Используя одно и то же разделение поезд / тест, мы можем обучить две новые модели с одинаковыми гиперпараметрами для индивидуального прогнозирования содержания свинца и меди. Тогда мы можем тренировать MultiOutputRegressor используя оба класса. И, наконец, сравните их все с оригинальной моделью. Вот так:

reg = GPR(RBF(), alpha=1)
reg.fit(X_train, y_train)
preds = reg.predict(X_test)
reg_lead = GPR(RBF(), alpha=1)
reg_lead.fit(X_train, y_train.lead)
lead_preds = reg_lead.predict(X_test)
reg_cop = GPR(RBF(), alpha=1)
reg_cop.fit(X_train, y_train.copper)
cop_preds = reg_cop.predict(X_test)
multi_reg = MultiOutputRegressor(GPR(RBF(), alpha=1))
multi_reg.fit(X_train, y_train)
multi_preds = multi_reg.predict(X_test)

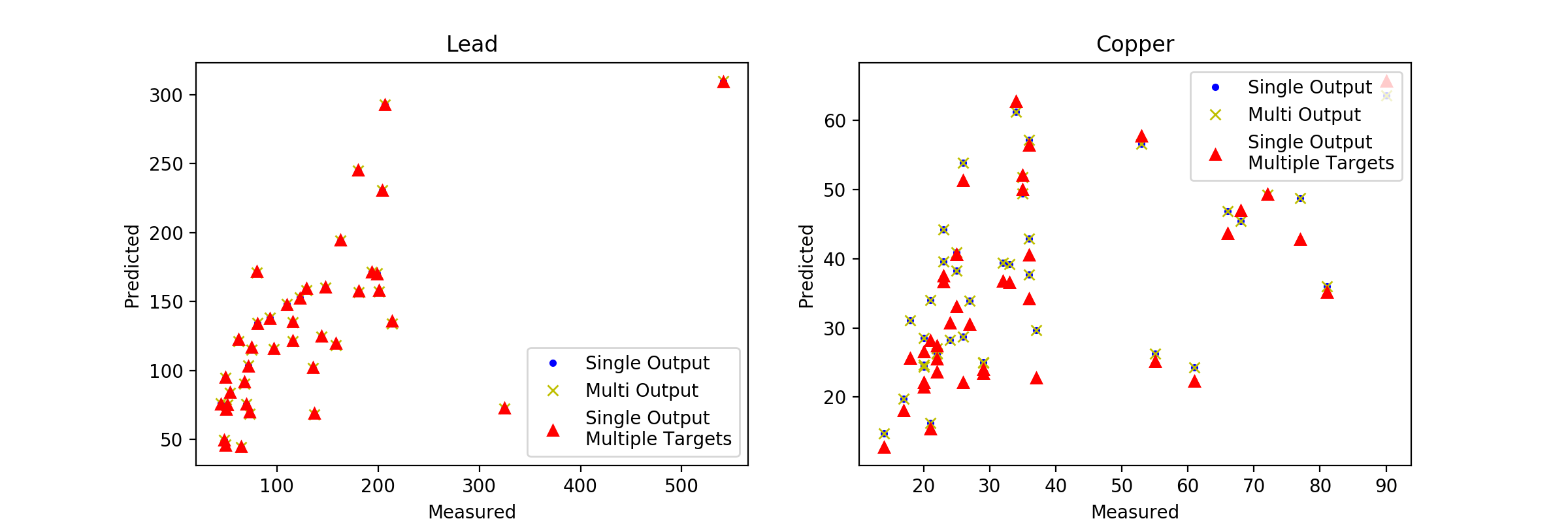
Теперь у нас есть несколько моделей, которые мы можем сравнить. Давайте построим прогнозы и посмотрим, что мы получим.

Интересно, что в прогнозах по лидерам нет видимой разницы, но в прогнозах по меди есть некоторые. И они существуют только между исходной моделью GPR и другими нашими моделями. Переходя к более количественным показателям погрешности, мы видим, что для объясненной дисперсии исходная модель работает немного лучше, чем наш MultiOutputRegressor. Интересно то, что объясненная дисперсия для модели из меди значительно ниже, чем для модели из свинца (это фактически соответствует поведению отдельных компонентов двух других моделей). Все это очень интересно и может привести нас к нескольким разным путям разработки к нашей окончательной модели.

Я думаю, что важным моментом здесь является то, что все итерации модели, по-видимому, находятся в одной и той же области, и в этом сценарии нет явного победителя. Это тот случай, когда вам нужно будет выполнить какой-то значительный поиск по сетке и, возможно, вам поможет реализация анизотропного ядра и любых других знаний, относящихся к конкретной области, но, поскольку это наш пример, он далек от полезной модели.