IR Рассчитать среднюю точность от варьирования соответствующих документов до ранга K

Question

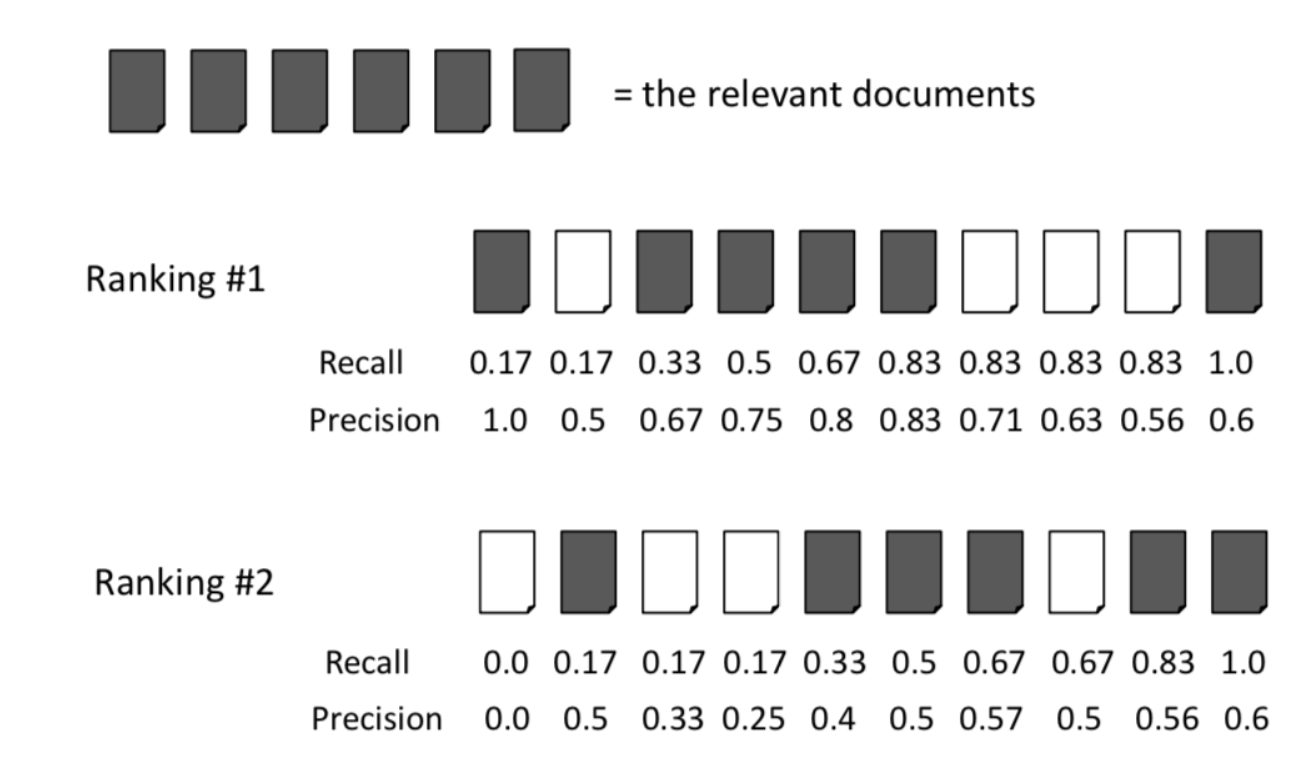
Приведенная выше диаграмма показывает стандартный пример точности и отзыва в настройке поиска документа.

Чтобы вычислить среднюю точность для ранга 1, вам достаточно сделать:

(1,0 + 0,67 + 0,75 + 0,8 + 0,83 + 0,6) / 6 = 0,78

Приведенный выше пример отлично подходит для небольших коллекций документов, но, скажем, у вас есть поисковая система с 100 000 документов, а запрос может содержать 100 релевантных документов. Как бы это было адаптировано, если бы вы сохранили длину K в 10?

Пример:

Было решено, что запрос для Ранжирования № 1 имеет 20 соответствующих документов, и это становится:

(1,0 + 0,67 + 0,75 + 0,8 + 0,83 + 0,6) / 20 = 0,23

или вы все еще делите на 6, потому что это число соответствующих документов в пределах ранга длины K?

Answer 1

Вы делите на общее количество соответствующих |R| даже если оно больше, чем ваша отсечка, К.

Это кажется немного глупым, но представьте, что ваша система вернула только 10 документов вместо того, чтобы вы решили сократить рейтинг в этот момент. AP хочет "наказать" эту систему по сравнению с той, которая получает больше документов.

В традиционной оценке IR вы устанавливаете K=1000 при расчете AP, и обычно |R| меньше 1000. В приведенном выше примере с домашним заданием / учебником цель состоит в том, чтобы вычислить вручную, чтобы у них было очень маленькое значение K, но при компьютерной оценке вы хотите получить такое большое значение K, которое будет разумным.

Существуют другие меры ранжирования, которые не имеют этой "проблемы", когда максимум не равен 1 во всех ситуациях, то есть NDCG @ K, который очень похож на AP, за исключением того, что он специально нормализован, то есть он всегда будет выводить 1 для наилучшего рейтинга в K и 0 для худшего рейтинга. Эта нормализация до наилучшего возможного ранжирования более понятна для объяснения людям, чем точки отзыва MAP, но показатели в реальной жизни сильно коррелируют.