Алгоритм возврата всех комбинаций k элементов из n
Я хочу написать функцию, которая принимает массив букв в качестве аргумента и количество этих букв для выбора.
Допустим, вы предоставляете массив из 8 букв и хотите выбрать 3 буквы из этого. Тогда вы должны получить:
8! / ((8 - 3)! * 3!) = 56
Взамен массивы (или слова), состоящие из 3 букв.
78 ответов
Искусство компьютерного программирования. Том 4: В Fascicle 3 есть тонна из них, которая может соответствовать вашей конкретной ситуации лучше, чем я описываю.
Серые коды
Проблема, с которой вы столкнетесь, - это, конечно, память и довольно быстро, у вас будут проблемы с 20 элементами в вашем наборе - 20 C3 = 1140. И если вы хотите перебрать набор, лучше всего использовать модифицированный серый закодируйте алгоритм, чтобы вы не держали их все в памяти. Они генерируют следующую комбинацию из предыдущего и избегают повторений. Есть много из них для различных целей. Мы хотим максимизировать различия между последовательными комбинациями? минимизировать? и так далее.
Некоторые из оригинальных работ, описывающих серые коды:
- Некоторые гамильтоновы пути и алгоритм минимального изменения
- Алгоритм генерации комбинации смежных обменов
Вот некоторые другие документы, освещающие эту тему:
- Эффективная реализация алгоритма генерации комбинаций Eades, Hickey, Read и смежных обменов (PDF, с кодом на Pascal)
- Комбинированные генераторы
- Обзор комбинаторных серых кодов (PostScript)
- Алгоритм для кодов серого
Чейз Твиддл (алгоритм)
Филип Дж. Чейз, " Алгоритм 382: комбинации М из N объектов" (1970)
Алгоритм в C...
Индекс комбинаций в лексикографическом порядке (алгоритм Buckles 515)
Вы также можете ссылаться на комбинацию по ее индексу (в лексикографическом порядке). Понимая, что индекс должен быть неким изменением справа налево на основе индекса, мы можем построить нечто, что должно восстановить комбинацию.
Итак, у нас есть набор {1,2,3,4,5,6}... и мы хотим три элемента. Допустим, {1,2,3} мы можем сказать, что разница между элементами одна и в порядке и минимальна. {1,2,4} имеет одно изменение и лексикографически номер 2. Таким образом, число "изменений" в последнем месте соответствует одному изменению в лексикографическом порядке. Второе место с одним изменением {1,3,4} имеет одно изменение, но учитывает большее изменение, поскольку оно находится на втором месте (пропорционально количеству элементов в исходном наборе).
Метод, который я описал, является деконструкцией, как кажется, от установки к индексу, нам нужно сделать обратное - что гораздо сложнее. Вот как Баксл решает проблему. Я написал несколько C для их вычисления с небольшими изменениями - я использовал индекс наборов, а не диапазон номеров, чтобы представить набор, поэтому мы всегда работаем от 0...n. Замечания:
- Поскольку комбинации неупорядочены, {1,3,2} = {1,2,3} - мы заказываем их как лексикографические.
- Этот метод имеет неявный 0, чтобы начать набор для первого различия.
Индекс комбинаций в лексикографическом порядке (McCaffrey)
Есть и другой способ: его концепцию легче понять и запрограммировать, но без оптимизации Buckles. К счастью, он также не создает дублирующихся комбинаций:
Набор  что максимизирует
что максимизирует 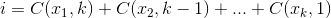 , где
, где 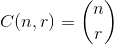 ,
,
Для примера: 27 = C(6,4) + C(5,3) + C(2,2) + C(1,1), Итак, 27-я лексикографическая комбинация из четырех вещей: {1,2,5,6}, это индексы любого набора, на который вы хотите посмотреть. Пример ниже (OCaml), требует choose функция, оставленная читателю:
(* this will find the [x] combination of a [set] list when taking [k] elements *)
let combination_maccaffery set k x =
(* maximize function -- maximize a that is aCb *)
(* return largest c where c < i and choose(c,i) <= z *)
let rec maximize a b x =
if (choose a b ) <= x then a else maximize (a-1) b x
in
let rec iterate n x i = match i with
| 0 -> []
| i ->
let max = maximize n i x in
max :: iterate n (x - (choose max i)) (i-1)
in
if x < 0 then failwith "errors" else
let idxs = iterate (List.length set) x k in
List.map (List.nth set) (List.sort (-) idxs)
В C#:
public static IEnumerable<IEnumerable<T>> Combinations<T>(this IEnumerable<T> elements, int k)
{
return k == 0 ? new[] { new T[0] } :
elements.SelectMany((e, i) =>
elements.Skip(i + 1).Combinations(k - 1).Select(c => (new[] {e}).Concat(c)));
}
Использование:
var result = Combinations(new[] { 1, 2, 3, 4, 5 }, 3);
Результат:
123
124
125
134
135
145
234
235
245
345
Краткое решение Java:
import java.util.Arrays;
public class Combination {
public static void main(String[] args){
String[] arr = {"A","B","C","D","E","F"};
combinations2(arr, 3, 0, new String[3]);
}
static void combinations2(String[] arr, int len, int startPosition, String[] result){
if (len == 0){
System.out.println(Arrays.toString(result));
return;
}
for (int i = startPosition; i <= arr.length-len; i++){
result[result.length - len] = arr[i];
combinations2(arr, len-1, i+1, result);
}
}
}
Результат будет
[A, B, C]
[A, B, D]
[A, B, E]
[A, B, F]
[A, C, D]
[A, C, E]
[A, C, F]
[A, D, E]
[A, D, F]
[A, E, F]
[B, C, D]
[B, C, E]
[B, C, F]
[B, D, E]
[B, D, F]
[B, E, F]
[C, D, E]
[C, D, F]
[C, E, F]
[D, E, F]
Могу ли я представить свое рекурсивное решение Python для этой проблемы?
def choose_iter(elements, length):
for i in xrange(len(elements)):
if length == 1:
yield (elements[i],)
else:
for next in choose_iter(elements[i+1:len(elements)], length-1):
yield (elements[i],) + next
def choose(l, k):
return list(choose_iter(l, k))
Пример использования:
>>> len(list(choose_iter("abcdefgh",3)))
56
Мне нравится это за его простоту.
Допустим, ваш массив букв выглядит так: "ABCDEFGH". У вас есть три индекса (i, j, k), указывающие, какие буквы вы собираетесь использовать для текущего слова. Вы начинаете с:
ABCDEFGH ^ ^ ^ IJK
Сначала вы меняете k, поэтому следующий шаг выглядит так:
ABCDEFGH ^ ^ ^ IJK
Если вы достигли конца, вы продолжаете и меняете j, а затем снова k.
ABCDEFGH ^ ^ ^ IJK ABCDEFGH ^ ^ ^ IJK
Как только вы достигли G, вы также начинаете меняться.
ABCDEFGH ^ ^ ^ IJK ABCDEFGH ^ ^ ^ IJK...
Написано в коде это выглядит примерно так
void print_combinations(const char *string)
{
int i, j, k;
int len = strlen(string);
for (i = 0; i < len - 2; i++)
{
for (j = i + 1; j < len - 1; j++)
{
for (k = j + 1; k < len; k++)
printf("%c%c%c\n", string[i], string[j], string[k]);
}
}
}
Следующий рекурсивный алгоритм выбирает все комбинации k-элементов из упорядоченного набора:
- выберите первый элемент
iвашей комбинации - скомбинировать
iс каждой из комбинацийk-1элементы, выбранные рекурсивно из набора элементов, больших чемi,
Повторите выше для каждого i в наборе.
Важно, чтобы вы выбрали остальные элементы как больше, чем i, чтобы избежать повторения. Таким образом, [3,5] будет выбран только один раз, как [3] в сочетании с [5], а не дважды (условие исключает [5] + [3]). Без этого условия вы получаете вариации вместо комбинаций.
Краткий пример на Python:
def comb(sofar, rest, n):
if n == 0:
print sofar
else:
for i in range(len(rest)):
comb(sofar + rest[i], rest[i+1:], n-1)
>>> comb("", "abcde", 3)
abc
abd
abe
acd
ace
ade
bcd
bce
bde
cde
Для объяснения рекурсивный метод описан в следующем примере:
Пример: A B C D E
Все комбинации из 3 будут:
- А со всеми комбинациями 2 из остальных (BCDE)
- B со всеми комбинациями 2 от остальных (CDE)
- C со всеми комбинациями 2 от остальных (D E)
В C++ следующая подпрограмма будет производить все комбинации длины (first,k) между диапазонами [first,last):
#include <algorithm>
template <typename Iterator>
bool next_combination(const Iterator first, Iterator k, const Iterator last)
{
/* Credits: Mark Nelson http://marknelson.us */
if ((first == last) || (first == k) || (last == k))
return false;
Iterator i1 = first;
Iterator i2 = last;
++i1;
if (last == i1)
return false;
i1 = last;
--i1;
i1 = k;
--i2;
while (first != i1)
{
if (*--i1 < *i2)
{
Iterator j = k;
while (!(*i1 < *j)) ++j;
std::iter_swap(i1,j);
++i1;
++j;
i2 = k;
std::rotate(i1,j,last);
while (last != j)
{
++j;
++i2;
}
std::rotate(k,i2,last);
return true;
}
}
std::rotate(first,k,last);
return false;
}
Это можно использовать так:
#include <string>
#include <iostream>
int main()
{
std::string s = "12345";
std::size_t comb_size = 3;
do
{
std::cout << std::string(s.begin(), s.begin() + comb_size) << std::endl;
} while (next_combination(s.begin(), s.begin() + comb_size, s.end()));
return 0;
}
Это напечатает следующее:
123
124
125
134
135
145
234
235
245
345
Я нашел эту ветку полезной и подумал, что добавлю решение Javascript, которое вы можете добавить в Firebug. В зависимости от вашего движка JS, если начальная строка велика, это может занять немного времени.
function string_recurse(active, rest) {
if (rest.length == 0) {
console.log(active);
} else {
string_recurse(active + rest.charAt(0), rest.substring(1, rest.length));
string_recurse(active, rest.substring(1, rest.length));
}
}
string_recurse("", "abc");
Вывод должен быть следующим:
abc
ab
ac
a
bc
b
c
static IEnumerable<string> Combinations(List<string> characters, int length)
{
for (int i = 0; i < characters.Count; i++)
{
// only want 1 character, just return this one
if (length == 1)
yield return characters[i];
// want more than one character, return this one plus all combinations one shorter
// only use characters after the current one for the rest of the combinations
else
foreach (string next in Combinations(characters.GetRange(i + 1, characters.Count - (i + 1)), length - 1))
yield return characters[i] + next;
}
}
Простой рекурсивный алгоритм в Haskell
import Data.List
combinations 0 lst = [[]]
combinations n lst = do
(x:xs) <- tails lst
rest <- combinations (n-1) xs
return $ x : rest
Сначала мы определим частный случай, т.е. выберем нулевые элементы. Он выдает один результат, который представляет собой пустой список (т. Е. Список, который содержит пустой список).
Для n > 0, x проходит через каждый элемент списка и xs каждый элемент после x,
rest кирки n - 1 элементы из xs используя рекурсивный вызов combinations, Конечным результатом функции является список, в котором каждый элемент x : rest (т.е. список, который имеет x как голова и rest как хвост) для каждого другого значения x а также rest,
> combinations 3 "abcde"
["abc","abd","abe","acd","ace","ade","bcd","bce","bde","cde"]
И, конечно, поскольку Haskell ленив, список постепенно генерируется по мере необходимости, поэтому вы можете частично оценить экспоненциально большие комбинации.
> let c = combinations 8 "abcdefghijklmnopqrstuvwxyz"
> take 10 c
["abcdefgh","abcdefgi","abcdefgj","abcdefgk","abcdefgl","abcdefgm","abcdefgn",
"abcdefgo","abcdefgp","abcdefgq"]
А вот и дедушка КОБОЛЬ, очень злобный язык.
Давайте предположим, что массив состоит из 34 элементов по 8 байтов каждый (чисто произвольный выбор). Идея состоит в том, чтобы перечислить все возможные комбинации из 4 элементов и загрузить их в массив.
Мы используем 4 индекса, по одному на каждую позицию в группе из 4
Массив обрабатывается так:
idx1 = 1
idx2 = 2
idx3 = 3
idx4 = 4
Мы меняем idx4 от 4 до конца. Для каждого idx4 мы получаем уникальную комбинацию из четырех групп. Когда idx4 подходит к концу массива, мы увеличиваем idx3 на 1 и устанавливаем idx4 в idx3 + 1. Затем мы снова запускаем idx4 до конца. Мы продолжаем таким образом, увеличивая idx3, idx2 и idx1 соответственно, пока позиция idx1 не станет меньше 4 от конца массива. Это завершает алгоритм.
1 --- pos.1
2 --- pos 2
3 --- pos 3
4 --- pos 4
5
6
7
etc.
Первые итерации:
1234
1235
1236
1237
1245
1246
1247
1256
1257
1267
etc.
Пример COBOL:
01 DATA_ARAY.
05 FILLER PIC X(8) VALUE "VALUE_01".
05 FILLER PIC X(8) VALUE "VALUE_02".
etc.
01 ARAY_DATA OCCURS 34.
05 ARAY_ITEM PIC X(8).
01 OUTPUT_ARAY OCCURS 50000 PIC X(32).
01 MAX_NUM PIC 99 COMP VALUE 34.
01 INDEXXES COMP.
05 IDX1 PIC 99.
05 IDX2 PIC 99.
05 IDX3 PIC 99.
05 IDX4 PIC 99.
05 OUT_IDX PIC 9(9).
01 WHERE_TO_STOP_SEARCH PIC 99 COMP.
* Stop the search when IDX1 is on the third last array element:
COMPUTE WHERE_TO_STOP_SEARCH = MAX_VALUE - 3
MOVE 1 TO IDX1
PERFORM UNTIL IDX1 > WHERE_TO_STOP_SEARCH
COMPUTE IDX2 = IDX1 + 1
PERFORM UNTIL IDX2 > MAX_NUM
COMPUTE IDX3 = IDX2 + 1
PERFORM UNTIL IDX3 > MAX_NUM
COMPUTE IDX4 = IDX3 + 1
PERFORM UNTIL IDX4 > MAX_NUM
ADD 1 TO OUT_IDX
STRING ARAY_ITEM(IDX1)
ARAY_ITEM(IDX2)
ARAY_ITEM(IDX3)
ARAY_ITEM(IDX4)
INTO OUTPUT_ARAY(OUT_IDX)
ADD 1 TO IDX4
END-PERFORM
ADD 1 TO IDX3
END-PERFORM
ADD 1 TO IDX2
END_PERFORM
ADD 1 TO IDX1
END-PERFORM.
Если вы можете использовать синтаксис SQL - скажем, если вы используете LINQ для доступа к полям структуры или массива или напрямую обращаетесь к базе данных, в которой есть таблица с именем "Алфавит", с одним полем "Буква", вы можете изменить следующее код:
SELECT A.Letter, B.Letter, C.Letter
FROM Alphabet AS A, Alphabet AS B, Alphabet AS C
WHERE A.Letter<>B.Letter AND A.Letter<>C.Letter AND B.Letter<>C.Letter
AND A.Letter<B.Letter AND B.Letter<C.Letter
Это вернет все комбинации из 3 букв, независимо от того, сколько букв у вас в таблице "Алфавит" (это может быть 3, 8, 10, 27 и т. Д.).
Если вам нужны все перестановки, а не комбинации (т.е. вы хотите, чтобы "ACB" и "ABC" считались как разные, а не появлялись только один раз), просто удалите последнюю строку (одну "И"), и все готово.
Постредактирование: перечитав вопрос, я понимаю, что нужен общий алгоритм, а не только конкретный для случая выбора 3 пунктов. Ответ Адама Хьюза является полным, к сожалению, я не могу его проголосовать (пока). Этот ответ прост, но работает только тогда, когда вам нужно ровно 3 элемента.
Еще одна версия C# с ленивым генерированием индексов комбинации. Эта версия поддерживает единый массив индексов для определения соответствия между списком всех значений и значениями для текущей комбинации, т. Е. Постоянно использует O(k) дополнительное пространство в течение всего времени выполнения. Код генерирует отдельные комбинации, включая первую, за O(k) время.
public static IEnumerable<T[]> Combinations<T>(this T[] values, int k)
{
if (k < 0 || values.Length < k)
yield break; // invalid parameters, no combinations possible
// generate the initial combination indices
var combIndices = new int[k];
for (var i = 0; i < k; i++)
{
combIndices[i] = i;
}
while (true)
{
// return next combination
var combination = new T[k];
for (var i = 0; i < k; i++)
{
combination[i] = values[combIndices[i]];
}
yield return combination;
// find first index to update
var indexToUpdate = k - 1;
while (indexToUpdate >= 0 && combIndices[indexToUpdate] >= values.Length - k + indexToUpdate)
{
indexToUpdate--;
}
if (indexToUpdate < 0)
yield break; // done
// update combination indices
for (var combIndex = combIndices[indexToUpdate] + 1; indexToUpdate < k; indexToUpdate++, combIndex++)
{
combIndices[indexToUpdate] = combIndex;
}
}
}
Тестовый код:
foreach (var combination in new[] {'a', 'b', 'c', 'd', 'e'}.Combinations(3))
{
System.Console.WriteLine(String.Join(" ", combination));
}
Выход:
a b c
a b d
a b e
a c d
a c e
a d e
b c d
b c e
b d e
c d e
Вот элегантная, обобщенная реализация в Scala, как описано в 99 Проблемах Scala.
object P26 {
def flatMapSublists[A,B](ls: List[A])(f: (List[A]) => List[B]): List[B] =
ls match {
case Nil => Nil
case sublist@(_ :: tail) => f(sublist) ::: flatMapSublists(tail)(f)
}
def combinations[A](n: Int, ls: List[A]): List[List[A]] =
if (n == 0) List(Nil)
else flatMapSublists(ls) { sl =>
combinations(n - 1, sl.tail) map {sl.head :: _}
}
}
У меня был алгоритм перестановки, который я использовал для проекта Euler, в Python:
def missing(miss,src):
"Returns the list of items in src not present in miss"
return [i for i in src if i not in miss]
def permutation_gen(n,l):
"Generates all the permutations of n items of the l list"
for i in l:
if n<=1: yield [i]
r = [i]
for j in permutation_gen(n-1,missing([i],l)): yield r+j
Если
n<len(l)
у вас должна быть вся необходимая комбинация без повторения, она вам нужна?
Это генератор, поэтому вы используете его примерно так:
for comb in permutation_gen(3,list("ABCDEFGH")):
print comb
Допустим, ваш массив букв выглядит так: "ABCDEFGH". У вас есть три индекса (i, j, k), указывающие, какие буквы вы собираетесь использовать для текущего слова. Вы начинаете с:
ABCDEFGH ^ ^ ^ IJK
Сначала вы меняете k, поэтому следующий шаг выглядит так:
ABCDEFGH ^ ^ ^ IJK
Если вы достигли конца, вы продолжаете и меняете j, а затем снова k.
ABCDEFGH ^ ^ ^ IJK ABCDEFGH ^ ^ ^ IJK
Как только вы достигли G, вы также начинаете меняться.
ABCDEFGH ^ ^ ^ IJK ABCDEFGH ^ ^ ^ IJK...
function initializePointers($cnt) {
$pointers = [];
for($i=0; $i<$cnt; $i++) {
$pointers[] = $i;
}
return $pointers;
}
function incrementPointers(&$pointers, &$arrLength) {
for($i=0; $i<count($pointers); $i++) {
$currentPointerIndex = count($pointers) - $i - 1;
$currentPointer = $pointers[$currentPointerIndex];
if($currentPointer < $arrLength - $i - 1) {
++$pointers[$currentPointerIndex];
for($j=1; ($currentPointerIndex+$j)<count($pointers); $j++) {
$pointers[$currentPointerIndex+$j] = $pointers[$currentPointerIndex]+$j;
}
return true;
}
}
return false;
}
function getDataByPointers(&$arr, &$pointers) {
$data = [];
for($i=0; $i<count($pointers); $i++) {
$data[] = $arr[$pointers[$i]];
}
return $data;
}
function getCombinations($arr, $cnt)
{
$len = count($arr);
$result = [];
$pointers = initializePointers($cnt);
do {
$result[] = getDataByPointers($arr, $pointers);
} while(incrementPointers($pointers, count($arr)));
return $result;
}
$result = getCombinations([0, 1, 2, 3, 4, 5], 3);
print_r($result);
Основано на /questions/26981161/algoritm-vozvrata-vseh-kombinatsij-k-elementov-iz-n/26981226#26981226, но более абстрактно, для указателей любого размера.
https://gist.github.com/3118596
Есть реализация для JavaScript. Он имеет функции для получения k-комбинаций и всех комбинаций массива любых объектов. Примеры:
k_combinations([1,2,3], 2)
-> [[1,2], [1,3], [2,3]]
combinations([1,2,3])
-> [[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3]]
Здесь у вас есть ленивая версия этого алгоритма, написанная на C#:
static bool nextCombination(int[] num, int n, int k)
{
bool finished, changed;
changed = finished = false;
if (k > 0)
{
for (int i = k - 1; !finished && !changed; i--)
{
if (num[i] < (n - 1) - (k - 1) + i)
{
num[i]++;
if (i < k - 1)
{
for (int j = i + 1; j < k; j++)
{
num[j] = num[j - 1] + 1;
}
}
changed = true;
}
finished = (i == 0);
}
}
return changed;
}
static IEnumerable Combinations<T>(IEnumerable<T> elements, int k)
{
T[] elem = elements.ToArray();
int size = elem.Length;
if (k <= size)
{
int[] numbers = new int[k];
for (int i = 0; i < k; i++)
{
numbers[i] = i;
}
do
{
yield return numbers.Select(n => elem[n]);
}
while (nextCombination(numbers, size, k));
}
}
И тестовая часть:
static void Main(string[] args)
{
int k = 3;
var t = new[] { "dog", "cat", "mouse", "zebra"};
foreach (IEnumerable<string> i in Combinations(t, k))
{
Console.WriteLine(string.Join(",", i));
}
}
Надеюсь, это поможет вам!
Clojure версия:
(defn comb [k l]
(if (= 1 k) (map vector l)
(apply concat
(map-indexed
#(map (fn [x] (conj x %2))
(comb (dec k) (drop (inc %1) l)))
l))))
Короткий код на Python, приводящий к позициям индекса
def yield_combos(n,k):
# n is set size, k is combo size
i = 0
a = [0 for i in range(k)]
while i > -1:
for j in range(i+1, k):
a[j] = a[j-1]+1
i=j
yield a
while a[i] == i + n - k:
i -= 1
a[i] += 1
Array.prototype.combs = function(num) {
var str = this,
length = str.length,
of = Math.pow(2, length) - 1,
out, combinations = [];
while(of) {
out = [];
for(var i = 0, y; i < length; i++) {
y = (1 << i);
if(y & of && (y !== of))
out.push(str[i]);
}
if (out.length >= num) {
combinations.push(out);
}
of--;
}
return combinations;
}
Алгоритм:
- Считайте от 1 до 2^n.
- Преобразуйте каждую цифру в ее двоичное представление.
- Переведите каждый бит "on" в элементы вашего набора, основываясь на позиции.
В C#:
void Main()
{
var set = new [] {"A", "B", "C", "D" }; //, "E", "F", "G", "H", "I", "J" };
var kElement = 2;
for(var i = 1; i < Math.Pow(2, set.Length); i++) {
var result = Convert.ToString(i, 2).PadLeft(set.Length, '0');
var cnt = Regex.Matches(Regex.Escape(result), "1").Count;
if (cnt == kElement) {
for(int j = 0; j < set.Length; j++)
if ( Char.GetNumericValue(result[j]) == 1)
Console.Write(set[j]);
Console.WriteLine();
}
}
}
Почему это работает?
Существует биекция между подмножествами n-элементного набора и n-битных последовательностей.
Это означает, что мы можем выяснить, сколько существует подмножеств, считая последовательности.
например, четыре элемента, представленные ниже, могут быть представлены {0,1} X {0, 1} X {0, 1} X {0, 1} (или 2^4) различными последовательностями.
Итак, все, что нам нужно сделать, это считать от 1 до 2 ^ n, чтобы найти все комбинации. (Мы игнорируем пустое множество.) Затем переведите цифры в их двоичное представление. Затем замените элементы вашего набора на "биты".
Если вы хотите получить только k элементов, выведите их только тогда, когда k битов включены.
(Если вы хотите, чтобы все подмножества вместо k подмножеств длины, удалите часть cnt/kElement.)
(В качестве доказательства см. Бесплатный учебный курс MIT по математике для информатики, Lehman и др., Раздел 11.2.2. https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-042j-mathematics-for-computer-science-fall-2010/readings/)
Все сказано и сделано, вот и код O'caml для этого. Алгоритм очевиден из кода..
let combi n lst =
let rec comb l c =
if( List.length c = n) then [c] else
match l with
[] -> []
| (h::t) -> (combi t (h::c))@(combi t c)
in
combi lst []
;;
Еще одно рекурсивное решение на Python.
def combination_indicies(n, k, j = 0, stack = []):
if len(stack) == k:
yield list(stack)
return
for i in range(j, n):
stack.append(i)
for x in combination_indicies(n, k, i + 1, stack):
yield x
stack.pop()
list(combination_indicies(5, 3))
Выход:
[[0, 1, 2],
[0, 1, 3],
[0, 1, 4],
[0, 2, 3],
[0, 2, 4],
[0, 3, 4],
[1, 2, 3],
[1, 2, 4],
[1, 3, 4],
[2, 3, 4]]
Вот метод, который дает вам все комбинации указанного размера из строки произвольной длины. Похоже на решение Кинмарса, но работает для различного ввода и k.
Код может быть изменен, чтобы обернуться, то есть 'dab' от ввода 'abcd' w k=3.
public void run(String data, int howMany){
choose(data, howMany, new StringBuffer(), 0);
}
//n choose k
private void choose(String data, int k, StringBuffer result, int startIndex){
if (result.length()==k){
System.out.println(result.toString());
return;
}
for (int i=startIndex; i<data.length(); i++){
result.append(data.charAt(i));
choose(data,k,result, i+1);
result.setLength(result.length()-1);
}
}
Выход для "abcde":
abc abd abe acd ace ade bcd bce bde cde
Короткая версия javascript (ES 5)
let combine = (list, n) =>
n == 0 ?
[[]] :
list.flatMap((e, i) =>
combine(
list.slice(i + 1),
n - 1
).map(c => [e].concat(c))
);
let res = combine([1,2,3,4], 3);
res.forEach(e => console.log(e.join()));
Вот код, который я недавно написал на Java, который вычисляет и возвращает все комбинации элементов "num" из элементов "outOf".
// author: Sourabh Bhat (heySourabh@gmail.com)
public class Testing
{
public static void main(String[] args)
{
// Test case num = 5, outOf = 8.
int num = 5;
int outOf = 8;
int[][] combinations = getCombinations(num, outOf);
for (int i = 0; i < combinations.length; i++)
{
for (int j = 0; j < combinations[i].length; j++)
{
System.out.print(combinations[i][j] + " ");
}
System.out.println();
}
}
private static int[][] getCombinations(int num, int outOf)
{
int possibilities = get_nCr(outOf, num);
int[][] combinations = new int[possibilities][num];
int arrayPointer = 0;
int[] counter = new int[num];
for (int i = 0; i < num; i++)
{
counter[i] = i;
}
breakLoop: while (true)
{
// Initializing part
for (int i = 1; i < num; i++)
{
if (counter[i] >= outOf - (num - 1 - i))
counter[i] = counter[i - 1] + 1;
}
// Testing part
for (int i = 0; i < num; i++)
{
if (counter[i] < outOf)
{
continue;
} else
{
break breakLoop;
}
}
// Innermost part
combinations[arrayPointer] = counter.clone();
arrayPointer++;
// Incrementing part
counter[num - 1]++;
for (int i = num - 1; i >= 1; i--)
{
if (counter[i] >= outOf - (num - 1 - i))
counter[i - 1]++;
}
}
return combinations;
}
private static int get_nCr(int n, int r)
{
if(r > n)
{
throw new ArithmeticException("r is greater then n");
}
long numerator = 1;
long denominator = 1;
for (int i = n; i >= r + 1; i--)
{
numerator *= i;
}
for (int i = 2; i <= n - r; i++)
{
denominator *= i;
}
return (int) (numerator / denominator);
}
}
Вот мое предложение в C++
Я пытался наложить как можно меньше ограничений на тип итератора, поэтому это решение предполагает только прямой итератор, и это может быть const_iterator. Это должно работать с любым стандартным контейнером. В случаях, когда аргументы не имеют смысла, он выдает std::invalid_argumnent
#include <vector>
#include <stdexcept>
template <typename Fci> // Fci - forward const iterator
std::vector<std::vector<Fci> >
enumerate_combinations(Fci begin, Fci end, unsigned int combination_size)
{
if(begin == end && combination_size > 0u)
throw std::invalid_argument("empty set and positive combination size!");
std::vector<std::vector<Fci> > result; // empty set of combinations
if(combination_size == 0u) return result; // there is exactly one combination of
// size 0 - emty set
std::vector<Fci> current_combination;
current_combination.reserve(combination_size + 1u); // I reserve one aditional slot
// in my vector to store
// the end sentinel there.
// The code is cleaner thanks to that
for(unsigned int i = 0u; i < combination_size && begin != end; ++i, ++begin)
{
current_combination.push_back(begin); // Construction of the first combination
}
// Since I assume the itarators support only incrementing, I have to iterate over
// the set to get its size, which is expensive. Here I had to itrate anyway to
// produce the first cobination, so I use the loop to also check the size.
if(current_combination.size() < combination_size)
throw std::invalid_argument("combination size > set size!");
result.push_back(current_combination); // Store the first combination in the results set
current_combination.push_back(end); // Here I add mentioned earlier sentinel to
// simplyfy rest of the code. If I did it
// earlier, previous statement would get ugly.
while(true)
{
unsigned int i = combination_size;
Fci tmp; // Thanks to the sentinel I can find first
do // iterator to change, simply by scaning
{ // from right to left and looking for the
tmp = current_combination[--i]; // first "bubble". The fact, that it's
++tmp; // a forward iterator makes it ugly but I
} // can't help it.
while(i > 0u && tmp == current_combination[i + 1u]);
// Here is probably my most obfuscated expression.
// Loop above looks for a "bubble". If there is no "bubble", that means, that
// current_combination is the last combination, Expression in the if statement
// below evaluates to true and the function exits returning result.
// If the "bubble" is found however, the ststement below has a sideeffect of
// incrementing the first iterator to the left of the "bubble".
if(++current_combination[i] == current_combination[i + 1u])
return result;
// Rest of the code sets posiotons of the rest of the iterstors
// (if there are any), that are to the right of the incremented one,
// to form next combination
while(++i < combination_size)
{
current_combination[i] = current_combination[i - 1u];
++current_combination[i];
}
// Below is the ugly side of using the sentinel. Well it had to haave some
// disadvantage. Try without it.
result.push_back(std::vector<Fci>(current_combination.begin(),
current_combination.end() - 1));
}
}
Для этого я создал решение в SQL Server 2005 и разместил его на своем веб-сайте: http://www.jessemclain.com/downloads/code/sql/fn_GetMChooseNCombos.sql.htm
Вот пример, чтобы показать использование:
SELECT * FROM dbo.fn_GetMChooseNCombos('ABCD', 2, '')
Результаты:
Word
----
AB
AC
AD
BC
BD
CD
(6 row(s) affected)