SaveDefinitions считается опасным
SaveDefinitions хороший вариант Manipulate, Это приводит Manipulate хранить любые определения, использованные для его создания, внутри панели "Манипуляции". Созданный таким образом Манипулятор может быть скопирован в пустой блокнот и все равно будет работать самостоятельно. Кроме того, ваша рабочая тетрадь, содержащая много таких манипуляций, также не превращается в розовую шкатулку с напечатанными сообщениями об ошибках под ней при открытии. Большой!
Тем не менее, вся эта доброта имеет свою темную сторону, которая может сильно укусить вас, если вы не знаете об этом. У меня было это в блокноте, над которым я работал несколько дней, но я представляю вам пошаговый пример сценария с игрушкой, который воссоздает проблему.
В этом сценарии вы хотите создать Manipulate показывает график хорошей волнистой функции, поэтому вы определяете это (пожалуйста, сделайте размер окна следующим, это важно):
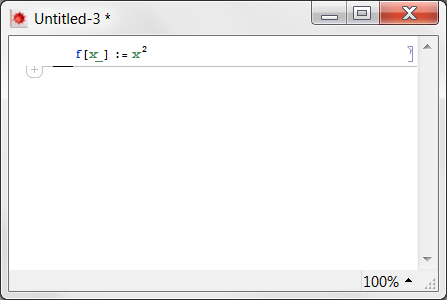
Определение хорошее, поэтому мы оставим его в следующий раз и сделаем его ячейкой инициализации. Далее мы добавим Manipulate и выполнить его тоже.
f[x_] := x^2
Manipulate[
Plot[n f[x], {x, -3, 3}],
{n, 1, 4},
SaveDefinitions -> True
]
Все отлично работает, Манипулятор действительно сияет, это хороший день.

Просто будучи вашим параноиком, вы проверяете правильность определения:
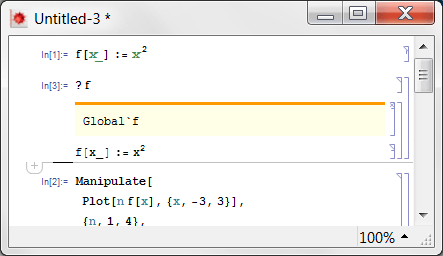
Да, все еще проверяется. Хорошо. Но теперь вам приходит в голову, что лучшая волнистая функция была бы синусом, поэтому вы меняете определение, выполняете и, будучи параноиком, проверяете:
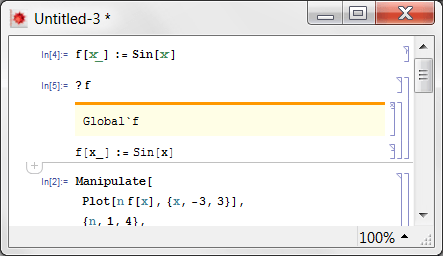
Все по-прежнему хорошо. Вы готовы после тяжелого рабочего дня, вы сохраняете свою работу и уходите. [Выйти из ядра]
Следующий день. Вы начинаете свою работу снова. Вы оцениваете ячейки инициализации в своей записной книжке. Определение все еще хорошо? Проверьте.
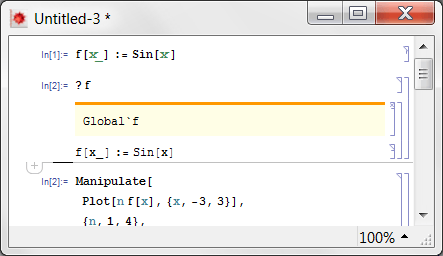
Теперь вы прокрутите вниз до окна "Манипуляции" (нет необходимости повторного выполнения благодаря SaveDefinitions), поиграйте немного с ползунком. И прокрутите назад.
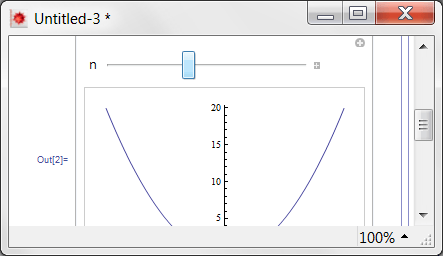
Будучи параноиком, вы еще раз проверяете определение f:
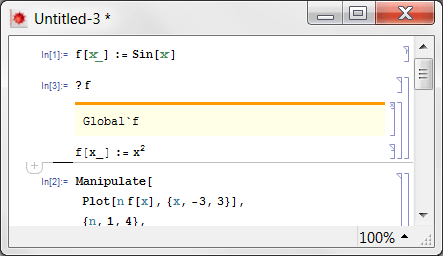
И вот, кто-то изменил определение за вашей спиной! И ничего не выполняется между вашим первым и вторым Information (?) проверить по номерам In[] (In[1]: def of f, In[2] первый?, In[3] второй?).
Что случилось? Ну, это Manipulate конечно. FullForm раскрывает свою внутреннюю структуру:
Manipulate[Plot[n*f[x],{x, -3, 3}],{{n, 2.44}, 1, 4},Initialization:>{f[x_] := x^2}]
Там у вас есть виновник. Часть инициализации блока снова определяет f, но это старая версия, потому что мы не переоценивали Manipulate после изменения его определения. Как только окно манипуляции появляется на экране, оно оценивается, и вы возвращаете свое старое определение. Во всем мире!
Конечно, в этом игрушечном примере сразу видно, что происходит что-то странное. В моем случае у меня был большой модуль в большом ноутбуке, в котором я после небольшой отладки изменил небольшую часть. Казалось, что это сработало, но на следующий день тот же баг, который меня подвел, прежде чем снова ударил. Мне потребовалось несколько часов, прежде чем я понял, что один из нескольких Манипуляторов, которые я использовал для изучения проблемы со всех сторон, делал это.
Очевидно, я испытываю желание сказать, что это нежелательное поведение. Теперь об обязательном вопросе: что мы можем сделать, чтобы предотвратить такое поведение Manipulate от возникновения, кроме повторного выполнения каждого Manipulate в вашей записной книжке каждый раз, когда вы меняете определение, которое они могут использовать?
2 ответа
Вот попытка. Идея состоит в том, чтобы идентифицировать символы с DownValues или какой-то другой ...Values внутри вашего манипулируемого кода, и автоматически переименовывайте их, используя вместо них уникальные переменные / символы. Идея здесь может быть выполнена довольно элегантно с помощью функции клонирования символов, что я нахожу полезным время от времени. Функция clone ниже будет клонировать данный символ, производя символ с такими же глобальными определениями:
Clear[GlobalProperties];
GlobalProperties[] :=
{OwnValues, DownValues, SubValues, UpValues, NValues, FormatValues,
Options, DefaultValues, Attributes};
Clear[unique];
unique[sym_] :=
ToExpression[
ToString[Unique[sym]] <>
StringReplace[StringJoin[ToString /@ Date[]], "." :> ""]];
Attributes[clone] = {HoldAll};
clone[s_Symbol, new_Symbol: Null] :=
With[{clone = If[new === Null, unique[Unevaluated[s]], ClearAll[new]; new],
sopts = Options[Unevaluated[s]]},
With[{setProp = (#[clone] = (#[s] /. HoldPattern[s] :> clone)) &},
Map[setProp, DeleteCases[GlobalProperties[], Options]];
If[sopts =!= {}, Options[clone] = (sopts /. HoldPattern[s] :> clone)];
HoldPattern[s] :> clone]]
Есть несколько вариантов реализации самой функции. Одним из них является введение функции с другим именем, принимая те же аргументы, что и Manipulate, сказать myManipulate, Я буду использовать другой: мягко перегрузить Manipulate с помощью UpValues какой-то пользовательской обертки, которую я представлю. Я назову это CloneSymbols, Вот код:
ClearAll[CloneSymbols];
CloneSymbols /:
Manipulate[args___,CloneSymbols[sd:(SaveDefinitions->True)],after:OptionsPattern[]]:=
Unevaluated[Manipulate[args, sd, after]] /.
Cases[
Hold[args],
s_Symbol /; Flatten[{DownValues[s], SubValues[s], UpValues[s]}] =!= {} :>
clone[s],
Infinity, Heads -> True];
Вот пример использования:
f[x_] := Sin[x];
g[x_] := x^2;
Обратите внимание, что для использования новой функциональности необходимо обернуть SaveDefinitions->True вариант в CloneSymbols обертка:
Manipulate[Plot[ f[n g[x]], {x, -3, 3}], {n, 1, 4},
CloneSymbols[SaveDefinitions -> True]]
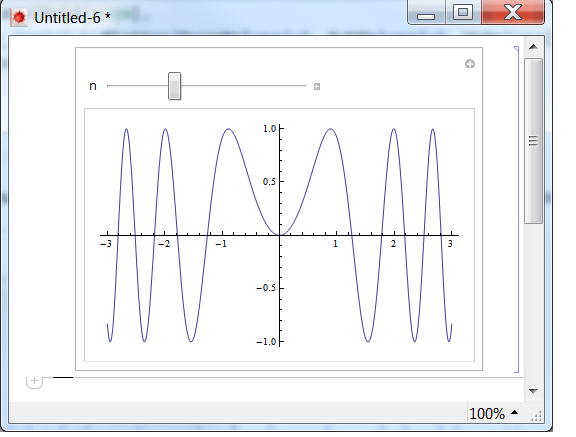
Это не повлияет на определения исходных символов в коде внутри Manipulate, поскольку это были их клоны, чьи определения были сохранены и теперь используются при инициализации. Мы можем посмотреть на FullForm за это Manipulate подтвердить, что:
Manipulate[Plot[f$37782011751740542578125[Times[n,g$37792011751740542587890[x]]],
List[x,-3,3]],List[List[n,1.9849999999999999`],1,4],RuleDelayed[Initialization,
List[SetDelayed[f$37782011751740542578125[Pattern[x,Blank[]]],Sin[x]],
SetDelayed[g$37792011751740542587890[Pattern[x,Blank[]]],Power[x,2]]]]]
В частности, вы можете изменить определения функций, чтобы сказать
f[x_]:=Cos[x];
g[x_]:=x;
Затем переместите ползунок Manipulate производится выше, а затем проверьте определения функций
?f
Global`f
f[x_]:=Cos[x]
?g
Global`g
g[x_]:=x
это Manipulate является достаточно независимым от чего-либо и может быть безопасно скопирован и вставлен. Здесь происходит следующее: сначала мы находим все символы с нетривиальными DownValues, SubValues или же UpValues (возможно, можно добавить OwnValues а также) и использовать Cases а также clone создавать своих клонов на лету. Затем мы заменяем лексически все клонированные символы их клонами внутри Manipulate, а затем пусть Manipulate сохраните определения для клонов. Таким образом, мы делаем "снимок" задействованных функций, но никак не влияем на исходные функции.
Уникальность клонов (символов) была рассмотрена с помощью unique функция. Обратите внимание, что в то время как Manipulate- полученные таким образом не угрожают исходным определениям функций, они, как правило, все еще зависят от них, поэтому нельзя считать их полностью независимыми от чего-либо. Нужно пройтись по дереву зависимостей и клонировать все символы там, а затем восстановить их взаимозависимости, чтобы создать полностью автономный "снимок" в Manipulate. Это выполнимо, но сложнее.
РЕДАКТИРОВАТЬ
По запросу @Sjoerd я добавляю код для случая, когда мы хотим, чтобы наш Manipulate-s обновлять изменения функции, но не хотят, чтобы они активно вмешивались и изменяли какие-либо глобальные определения. Я предлагаю вариант техники "указателя": мы снова заменим имена функций новыми символами, но вместо того, чтобы клонировать эти новые символы после наших функций, мы будем использовать Manipulate"s Initialization возможность просто сделать эти символы "указатели" на наши функции, например, как Initialization:>{new1:=f,new2:=g}, Очевидно, что повторная оценка такого кода инициализации не может повредить определениям f или же gи в то же время наши Manipulate-s станет реагировать на изменения в этих определениях.
Первая мысль заключается в том, что мы могли бы просто заменить имена функций новыми символами и позволить Manipulate инициализация автоматически сделает все остальное. К сожалению, в этом процессе он обходит дерево зависимостей, и, следовательно, также будут включены определения для наших функций - чего мы и стараемся избегать. Таким образом, вместо этого мы явно построим Initialize вариант. Вот код:
ClearAll[SavePointers];
SavePointers /:
Manipulate[args___,SavePointers[sd :(SaveDefinitions->True)],
after:OptionsPattern[]] :=
Module[{init},
With[{ptrrules =
Cases[Hold[args],
s_Symbol /; Flatten[{DownValues[s], SubValues[s], UpValues[s]}] =!= {} :>
With[{pointer = unique[Unevaluated[s]]},
pointer := s;
HoldPattern[s] :> pointer],
Infinity, Heads -> True]},
Hold[ptrrules] /.
(Verbatim[HoldPattern][lhs_] :> rhs_ ) :> (rhs := lhs) /.
Hold[defs_] :>
ReleaseHold[
Hold[Manipulate[args, Initialization :> init, after]] /.
ptrrules /. init :> defs]]]
С теми же определениями, что и раньше:
ClearAll[f, g];
f[x_] := Sin[x];
g[x_] := x^2;
Вот FullForm произведено Manipulate:
In[454]:=
FullForm[Manipulate[Plot[f[n g[x]],{x,-3,3}],{n,1,4},
SavePointers[SaveDefinitions->True]]]
Out[454]//FullForm=
Manipulate[Plot[f$3653201175165770507872[Times[n,g$3654201175165770608016[x]]],
List[x,-3,3]],List[n,1,4],RuleDelayed[Initialization,
List[SetDelayed[f$3653201175165770507872,f],SetDelayed[g$3654201175165770608016,g]]]]
Вновь созданные символы служат "указателями" на наши функции. Manipulate-s, построенные с использованием этого подхода, будут реагировать на обновления в наших функциях и в то же время безвредны для определений основных функций. Платой является то, что они не являются автономными и не будут отображаться правильно, если основные функции не определены. Таким образом, можно использовать либо CloneSymbols обертка или SavePointersв зависимости от того, что нужно.
Ответ заключается в использовании ячейки инициализации в качестве инициализации для Manipulate:
Manipulate[
Plot[n f[x], {x, -3, 3}], {n, 1, 4},
Initialization :> FrontEndTokenExecute["EvaluateInitialization"]]
Вы также можете использовать DynamicModule:
DynamicModule[{f},
f[x_] := x^2;
Manipulate[Plot[n f[x], {x, -3, 3}], {n, 1, 4}]]
Вы не должны SaveDefinitions -> True в этом случае.
РЕДАКТИРОВАТЬ
В ответ на комментарий Шёрда. Используя следующую простую технику, вам не нужно копировать определение везде и обновлять все копии, если вы измените определение (но вам все равно нужно пересмотреть свой код, чтобы получить обновление Manipulate):
DynamicModule[{f}, f[x_] := x^2;
list = Manipulate[Plot[n^# f[x], {x, -3, 3}], {n, 2, 4}] & /@ Range[3]];
list // Row