Пролог бинарного дерева поиска - сравнение родительских узлов нежелательных родителей
Я новичок Пролог, пожалуйста, имейте это в виду. Я пытаюсь написать предикат, чтобы определить, является ли какой-то данный термин двоичным деревом поиска. Я понял этот код:
is_btree(nil).
is_btree(node(N,L,R)) :-
number(N),
is_btree(L),
is_btree(R),
small(N, R),
big(N, L).
small(N, nil).
small(N, node(M,L,R)) :-
N < M,
small(N, L),
small(N, R).
big(N, nil).
big(N, node(M,L,R)) :-
N > M,
big(N, L),
big(N, R).
Это работает довольно хорошо, пока я не протестирую граф, у которого есть узел с правой стороны, который проходит условие "выше, чем родительский узел", но он выше или равен родительскому узлу родительского узла. В этом случае Пролог сообщает об ошибке.
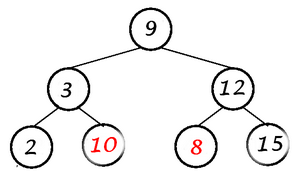
Вот пример запроса, который неожиданно завершается:
?- is_btree(node(9,node( 3,node( 2,nil,nil),
node(10,nil,nil)),
node(12,node( 8,nil,nil),
node(15,nil,nil)))).
false.
Очень похожая проблема возникает, когда некоторый узел на левой стороне выше родительского узла родительского узла - ситуация, показанная на следующем рисунке:
Как я могу проверить значения узлов только по значению их непосредственного родительского узла, но не по значениям родителей родителей?
5 ответов
Этот ответ непосредственно следует за этим предыдущим ответом, в частности, комментарием @WillNess, в котором предлагалось "[...] поменять две цели, поэтому обход прекращается как можно скорее, если [...] неудача chain перед phrase [...]".
lazy_chain/2 как chain/2, но использует пролог-сопрограммирование для ожидания достаточной реализации:
: - use_module ( библиотека (clpfd)). lazy_chain (Zs, R_2): - ( var (R_2) -> экземпляр_ошибки (R_2); clpfd:chain_relation(R_2) -> заморозить (Zs, lazy_chain_aux(Zs,R_2)); иначе -> domain_error (chain_reror, R_2), lazy_chain_aux([], _). lazy_chain_aux([Z0|Zs], R_2):- заморозить (Zs, lazy_chain_aux_(Zs,R_2,Z0)). lazy_chain_aux_([], _, _). lazy_chain_aux_([Z1|Zs], R_2, Z0):- вызов (R_2, Z0, Z1), заморозка (Zs, lazy_chain_aux_(Zs,R_2,Z1)).
На основе lazy_chain/2 мы определяем is_bintreeL/2 как это:
is_bintreeL (T): - lazy_chain (Zs, # <), фраза (in_order(T), Zs).
Так что... как насчет "раннего провала"?
? - T = узел (2, ноль, узел (1, ноль, узел (3, ноль, узел (4, ноль, узел (5, ноль, узел) (6, ноль, узел (7, ноль, узел (8, ноль, узел (9, ноль, узел (10, ноль, узел (11, ноль, узел (12, ноль, узел (13, ноль), узел (14, ноль, узел (15, ноль, узел (16, ноль, узел (17, ноль, узел (18, ноль, узел (19, ноль, узел (20, ноль, узел (21, ноль, узел) (22, ноль, узел (23, ноль, узел (24, ноль, узел, (25, ноль, узел (26, ноль, узел (27, ноль, узел (28, ноль, узел (29, ноль, узел (30, ноль), узел (31, ноль, узел (32, ноль, узел (33, ноль, узел (34, ноль, узел (35, ноль, узел (36, ноль, узел (37, ноль, узел) (38, ноль, узел (39, ноль, узел (40, ноль, узел (41, ноль, узел (42, ноль, узел (43, ноль, узел (44, ноль, узел (45, ноль, узел (46, ноль, узел) (47, ноль, узел (48, ноль, узел (49, ноль, узел) (50, ноль, узел (51, ноль, узел (52, ноль, узел (53, ноль, узел (54, ноль, узел (55, ноль, узел) (56, ноль, узел (57, ноль, узел (58, ноль, узел (59, ноль, узел (60, ноль, узел (61, ноль, узел (62, ноль, узел) (63, ноль, узел (64, ноль, узел (65, ноль, узел (66, ноль, узел (67, ноль, узел (68, ноль, узел (69, ноль, узел (70, ноль, узел (71, ноль, узел) (72, ноль, узел (73, ноль, узел (74, ноль, узел (75, ноль, узел (76, ноль, узел) (77, ноль, узел (78, ноль, узел (79, ноль, узел (80, ноль, узел (81, ноль, узел (82, ноль, узел (83, ноль, узел (84, ноль, узел (85, ноль, узел) (86, ноль, узел (87, ноль, узел (88, ноль), узел (89, ноль, узел (90, ноль, узел (91, ноль, узел (92, ноль, узел (93, ноль), узел (94, ноль, узел (95, ноль, узел (96, ноль, узел) (97, ноль, узел (98, ноль, узел (99, ноль, узел (100, ноль, ноль))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))), время ((фраза (in_order(T),Zs), нетерпеливый _chain (Zs, # <))). % 210 выводов, 0,000 CPU за 0,000 секунд (98% CPU, 4100201 Lips) ложный.?- T = узел (2, ноль, узел (1, ноль, узел (3, ноль, узел (4, ноль, узел (5, ноль, узел) (6, ноль, узел (7, ноль, узел (8, ноль, узел (9, ноль, узел (10, ноль, узел (11, ноль, узел (12, ноль, узел (13, ноль), узел (14, ноль, узел (15, ноль, узел (16, ноль, узел (17, ноль, узел (18, ноль, узел (19, ноль, узел (20, ноль, узел (21, ноль, узел) (22, ноль, узел (23, ноль, узел (24, ноль, узел, (25, ноль, узел (26, ноль, узел (27, ноль, узел (28, ноль, узел (29, ноль, узел (30, ноль), узел (31, ноль, узел (32, ноль, узел (33, ноль, узел (34, ноль, узел (35, ноль, узел (36, ноль, узел (37, ноль, узел) (38, ноль, узел (39, ноль, узел (40, ноль, узел (41, ноль, узел (42, ноль, узел (43, ноль, узел (44, ноль, узел (45, ноль, узел (46, ноль, узел) (47, ноль, узел (48, ноль, узел (49, ноль, узел) (50, ноль, узел (51, ноль, узел (52, ноль, узел (53, ноль, узел (54, ноль, узел (55, ноль, узел) (56, ноль, узел (57, ноль, узел (58, ноль, узел (59, ноль, узел (60, ноль, узел (61, ноль, узел (62, ноль, узел) (63, ноль, узел (64, ноль, узел (65, ноль, узел (66, ноль, узел (67, ноль, узел (68, ноль, узел (69, ноль, узел (70, ноль, узел (71, ноль, узел) (72, ноль, узел (73, ноль, узел (74, ноль, узел (75, ноль, узел (76, ноль, узел) (77, ноль, узел (78, ноль, узел (79, ноль, узел (80, ноль, узел (81, ноль, узел (82, ноль, узел (83, ноль, узел (84, ноль, узел (85, ноль, узел) (86, ноль, узел (87, ноль, узел (88, ноль), узел (89, ноль, узел (90, ноль, узел (91, ноль, узел (92, ноль, узел (93, ноль), узел (94, ноль, узел (95, ноль, узел (96, ноль, узел) (97, ноль, узел (98, ноль, узел (99, ноль, узел (100, ноль, ноль))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))), время ((lazy _chain (Zs, # <), фраза (in_order (T), Zs))). % 52 выводов, 0,000 CPU за 0,000 секунд (98% CPU, 1225664 Lips) ложный.
Лень побеждает - по крайней мере, в вышеуказанном случае:)
Обратите внимание, однако, что с помощью lazy_chain/2 с dcg может привести к ошибкам, которые трудно найти!
Для более надежного решения см. Этот альтернативный ответ...
Для полноты вот исходный код eager_chain/2:
eager_chain (Zs, R_2): - (var (R_2) -> instantiation_error (R_2); clpfd:chain_relation(R_2) -> eager_chain_aux (Zs, R_2); в противном случае -> domain_error(chain_relation, R_2)). eager_chain_aux([], _). eager_chain_aux([Z0|Zs], R_2):- eager_chain_aux_(Zs, R_2, Z0). eager_chain_aux_([], _, _). eager_chain_aux_([Z1|Zs], R_2, Z0):- вызов (R_2, Z0, Z1), eager_chain_aux_(Zs, R_2, Z1).
Вот немного другой взгляд на проблему, которую вы хотите решить.
DCG для сбора элементов: в порядке обхода дерева
in_order (nil) -> []. in_order(узел (X,L,R)) -> in_order (L), [X], in_order (R).
clpfd для связывания смежных элементов списка (которые являются переменными конечной области)
цепь (Zs, #<)
Давайте сложим все вместе и определим is_bintreeFD/1 как это:
: - use_module( библиотека (clpfd)). is_bintreeFD (T): - фраза(in_order(T), Zs), цепь(Zs, #<).
Примеры запросов:
?- is_bintreeFD(узел (9, узел ( 3, узел (2, ноль, ноль)), узел (10, ноль, ноль)), узел (12, узел (8, ноль, ноль), узел (15, ноль, ноль)))).ложь?- is_bintreeFD(узел (9, узел ( 3, узел (2, ноль, ноль)), узел ( 8, ноль, ноль)), узел (12, узел (10, ноль, ноль), узел (15, ноль, ноль)))). правда.
В комментарии к этому предыдущему ответу @WillNess предложил добавить "досрочный сбой" в качестве функции.
in_order_inf_sup//3 эффективно совмещает in_order//1 а также chain/2:
:- use_module(library(clpfd)).
in_order_inf_sup(nil, P, P) --> [].
in_order_inf_sup(node(X,L,R), P0, P) -->
in_order_inf_sup(L, P0, P1),
[X],
{ P1 #< X },
in_order_inf_sup(R, X, P).
Примеры запросов (как в предыдущем ответе):
?- фраза (in_order_inf_sup (узел (9, узел ( 3, узел (2, ноль, ноль)), узел (10, ноль, ноль)),
узел (12, узел (8, ноль, ноль), узел (15, ноль, ноль))),_,_),
Zs).
ложь?- фраза (in_order_inf_sup (узел (9, узел ( 3, узел (2, ноль, ноль)), узел ( 8, ноль, ноль)),
узел (12, узел (10, ноль, ноль), узел (15, ноль, ноль))),_,_),
Zs).
Zs = [2,3,8,9,10,12,15].
В этом ответе мы используем clpfd для декларативной целочисленной арифметики.
: - use_module ( библиотека (clpfd)). : - asserta ( clpfd: full_answer).
Мы определяем предикаты is_bintree/1 а также bintree_in/2 как это:
is_bintree (T): - bintree_in (T, _). bintree_in (ноль, LB-UB):- % LB-UB обозначает открытый интервал (LB, UB) LB # <;; UB. %, что все целые числа I, что LB #>; LB, Mid # <;; UB, bintree_in(L, LB-Mid), bintree_in(R, Mid-UB).
Сначала мы тестируем 1,2 дерева, заданного ОП:
|? - bintree_in (узел (9, узел ( 3, узел (2, ноль, ноль)), узел (10, ноль, ноль)),
узел (12, узел (8, ноль, ноль), узел (15, ноль, ноль))), _).
нет
Давайте исправим дерево и проверим снова!
|? - bintree_in (узел (9, узел ( 3, узел (2, ноль, ноль), узел (8, ноль, ноль)),
узел (12, узел (10, ноль, ноль), узел (15, ноль, ноль))), _).
_A в инф..1, _B в 16..суп?; % (несколько небрежно)
нет
ХОРОШО! Далее несколько угловых случаев:
|? - bintree_in (T, 0-0). % нет решения (как и ожидалось) нет |?- bintree_in(T, 0-1). % пустое дерево Т = ноль?; нет |?- bintree_in(T, 0-2). % одиночного дерева Т = ноль?; T = узел (1, ноль, ноль)?; нет
Обратите внимание, что в то время как is_btree/1 могу только "проверить", bintree_in/2 можно как 3 "тестировать", так и "генерировать"!
Итак, давайте сгенерируем (все возможные) двоичные деревья определенного размера в небольшом домене:
|? - bintree_in (T, 0-3). % T имеет менее 3 элементов Т = ноль?; T = узел (_A, ноль, ноль), _A в 1..2?; T = узел (1, ноль, узел (2, ноль, ноль))?; T = узел (2, узел (1, ноль, ноль), ноль)?; нет |?- bintree_in(T, 0-4). % T имеет менее 4 элементов Т = ноль?; T = узел (_A, ноль, ноль), _A в 1..3?; T = узел (_A, ноль, узел (_B, ноль, ноль)), _A # = <_ B + -1, _B #> = _ A + 1, _B в 2..3, _A в 1..2?; T = узел (1, ноль, узел (2, ноль, узел ( 3, ноль, ноль)))?; T = узел (1, ноль, узел ( 3, узел (2, ноль, ноль), ноль))?; T = узел (_A, узел (_B, ноль, ноль), ноль), _A#>=_B+1, _A в 2..3, _B в 1..2?; T = узел (2, узел (1, ноль, ноль), узел ( 3, ноль, ноль))?; T = узел ( 3, узел (1, ноль, узел (2, ноль, ноль)), ноль)?; T = узел ( 3, узел (2, узел (1, ноль, ноль), ноль), ноль)?; нет
Наконец, мы генерируем варианты решения с bintree_in/2 и проверить это с is_btree/1!
is_btree/1 нуждается в достаточной реализации; labeling/2 предоставляет нам основные условия.
|? - call_time ((UB в 2..12, индомен (UB), bintree_in (T, 0-UB), term_variables (T, Zs), маркировка ([], Zs), \+ is_btree(T); правда), T_ms). T_ms = 6270?; нет
Сноска 1: Код в этом ответе работает (на /questions/tagged/sicstus-prolog и swi-prolog.
Сноска 2: Все представленные выходные данные пролог-верхнего уровня - это SICStus Prolog 4.3.2 (64-бит).
Сноска 3: Не только делать оба, но (почти) произвольно смешивать генерацию и тестирование, так как он может обрабатывать частично реализованные термины.
Но это должно провалиться. Это дерево является недействительным BST и ваши предикатные тесты для действительных BST.
Здесь есть что сделать. Прямо сейчас вы выполняете два прохода над деревом - сначала в is_btreeво-вторых, с small/big,
Два могут быть объединены в одно, но сразу очевидное решение будет делать именно то, что вы хотите, и, таким образом, преуспеет на таких недействительных BST:
is_bst(nil).
is_bst(node(N,L,R)):-
( L = nil
; L = node(M,LL,LR), M < N, is_bst(L), ....
),
( R = nil
; ......
).
Чтобы исправить это, мы должны вернуть еще один результат из обхода дерева - это самый правый элемент дерева - и использовать его в сравнениях для проверки.
(edit: пропущено, что самый левый элемент также должен быть возвращен)