Числа Хэмминга для скорости O(N) и памяти O(1)

Question

Отказ от ответственности: есть много вопросов по этому поводу, но я не нашел ни одного с требованием постоянной памяти.

Числа Хэмминга это числа 2^i*3^j*5^kгде i, j, k - натуральные числа.

Есть ли возможность генерировать N-е число Хэмминга с O(N) временем и O(1) (постоянной) памятью? Под генерацией я подразумеваю именно генератор, то есть вы можете только выводить результат и не читать ранее сгенерированные числа (в этом случае память будет не постоянной). Но вы можете сохранить некоторое их постоянное количество.

Я вижу только лучший алгоритм с постоянной памятью не лучше, чем O(N log N), например, по приоритетной очереди. Но есть ли математическое доказательство того, что невозможно построить алгоритм за O(N) времени?

Answer 1

Первое, что следует рассмотреть здесь, - это алгоритм прямого перечисления срезов, который можно увидеть, например, в этом ответе SO, перечисляющем тройки. (k,j,i) вблизи заданного логарифмического значения (основание 2) члена последовательности, так что target - delta < k*log2_5 + j*log2_3 + i < target + delta, постепенно вычисляя совокупный логарифм, выбирая j а также k чтобы i прямо известно.

Таким образом, это N ² / ^3- время, производящее срезы N ² /3-всей последовательности за один раз (с k*log2_5 + j*log2_3 + i близко к целевому значению, так что эти тройки образуют корку тетраэдра, заполненного тройками последовательности Хемминга ¹), что означает время O(1) на произведенное число, таким образом производя N членов последовательности за O(N) амортизированное время и O(N) ^2/3) -пространство. Это не улучшение по сравнению с базовым алгоритмом Дейкстры ² с теми же сложностями, даже без амортизации и с лучшими постоянными коэффициентами.

Чтобы сделать это O(1) -пространством, ширину коры нужно будет сужать по мере продвижения по последовательности. Но чем уже корка, тем больше и больше будет промахов при перечислении троек - и это в значительной степени доказательство, о котором вы просили. Постоянный размер среза означает работу O (N ^2/3) на срез O(1), для общего O (N ^5/3) амортизированного времени, O(1) пространственного алгоритма.

Это две конечные точки в этом спектре: от времени N ¹, пространства N ^2/3 до пространства N ⁰, времени N ^5/3, амортизированные.

---

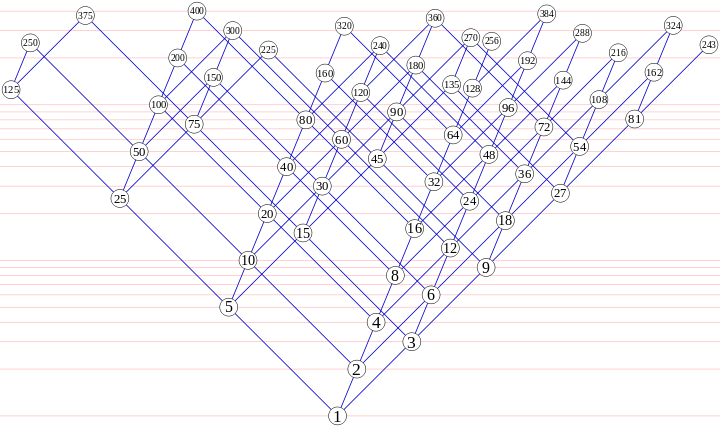
¹ Вот изображение из Википедии, с логарифмической вертикальной шкалой:

По сути, это тетраэдр троек последовательности Хемминга. (i,j,k) растягивается в пространстве как (i*log2, j*log3, k*log5) видно со стороны. Изображение немного искривлено, если это действительно 3D-картинка.

edit: ² Кажется, я забыл, что фрагменты должны быть отсортированы, так как они производятся в порядке j, k- перечисления. Это изменяет наилучшую сложность для создания N чисел последовательности по порядку с помощью алгоритма среза на время O (N ^2/3 log N), пространство O (N ^2/3) и делает алгоритм Дейкстры победителем. Это не меняет верхнюю границу времени O (N ^5/3) для срезов O(1).