Насосная лемма (Обычный язык)

Question

Мне нужна помощь с проблемой прокачки леммы.

L = { {a,b,c}* | #a(L) < #b(L) < #c(L) }

Это то, что я получил так далеко:

y = uvw is the string from the pumping lemma.

Я положил у = abbc^n, n - длина из леммы прокачки. y находится в L, потому что число a: s меньше, чем число b: s, а число b: s меньше, чем число c:s.

Я позволю u = a, v = bb и w = c^n. | Уф | <у, как указано в лемме прокачки. Если я "насос" (BB) ^ 2, то я получаю

y = abbbbc^n which violates the rule #b(L) < #c(L).

Это правильно? Я нахожусь на "правильном пути"?

Спасибо

Answer 1

Основная идея леммы прокачки состоит в том, чтобы сказать вам, что когда у вас есть регулярный язык L с бесконечным числом терминов в языке есть образец, который повторяется вечно.

Регулярное выражение, связанное с этим языком, будет содержать KLEENE-STAR(шаблон).

Автомат, связанный с этим регулярным выражением (и языком), будет содержать цикл.

Доказательство выполняется по принципу голубя.

это 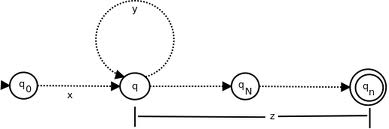очень наводит на мысль.

Обратите внимание, что в этом случае все члены должны начинаться с q0 и заканчиваться на qn. Итак, автоматы, определяющие язык, конечны (максимум N состояний), поэтому существует ограниченное количество состояний, но слова (т.е. термины) могут иметь>N букв. Принцип голубя говорит нам, что должно быть состояние, которое достигается 2 раза, поэтому в этом состоянии будет присутствовать цикл.

В вашей записи вы можете сделать соответствие с изображением так:

• ваш u является x из изображения

• v является y в изображении

• w является z из изображения

Прибыть из q0 в qn, вы можете использовать любую из строк из набора: { uw , uvw, uvvw, uvvvw, ... },

В этом конкретном случае картина P является y, набор X является {xz xyz xyyz xyyyz ...} а также S является length(x)+length(y),