Полиномы Лагерра в python с использованием scipy, отсутствие сходимости?

Кажется, что полиномы Лагерра не сходятся в некоторых порядках, что можно продемонстрировать, выполнив следующий код.

import numpy as np
from sympy import mpmath as mp
from scipy.special import genlaguerre as genlag
from sympy.mpmath import laguerre as genlag2
from matplotlib import pyplot as plt

def laguerre(x, r_ord, phi_ord, useArbitraryPrecision=False):
    if (r_ord < 30 and phi_ord < 30) and not useArbitraryPrecision:
        polyCoef = genlag(r_ord, phi_ord)
        out = np.polyval(polyCoef, x)
    else:
        fun = lambda arg: genlag2(r_ord, phi_ord, arg)
        fun2 = np.frompyfunc(genlag2, 3, 1)
        # fun2 = np.vectorize(fun)
        out = fun2(r_ord, phi_ord, x)
    return out

r_ord = 29
phi_ord = 29
f = lambda x, useArb : mp.log10(laguerre(x, 29, 29, useArb))
mp.plot(lambda y : f(y, True) - f(y, False), [0, 200], points = 1e3)
plt.show()

Мне было интересно, если кто-нибудь знал, что происходит или какие-либо ограничения точности scipy функционировать? Вы рекомендуете мне просто использовать mpmath функционировать? Сначала я подумал, что, возможно, после определенного заказа он не работает, но для (100, 100) он, кажется, работает просто отлично.

запустив

mp.plot([lambda y : f(y, True), lambda y: f(y, False)], [0, 200], points = 1e3)

Вы получаете следующее изображение, где расхождение становится довольно ясным.

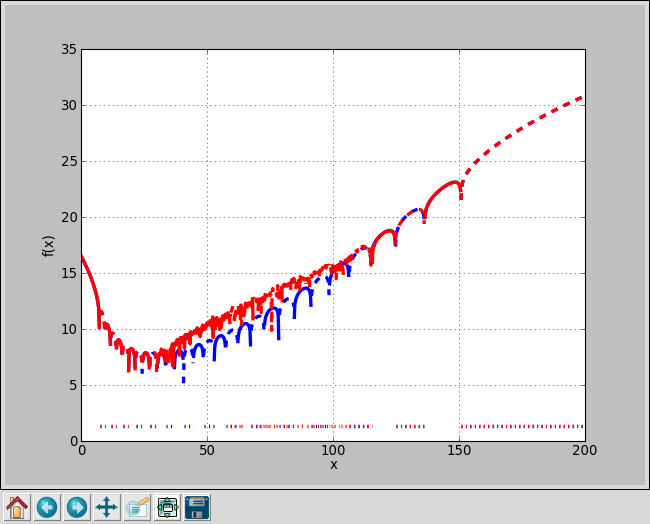
Любая помощь приветствуется.

Дайте мне знать, если что-то нужно уточнить.

Источник

2 ответа

Решение

С помощью polyval с полиномами высокого порядка (о n > 20) вообще плохая идея, потому что оценка полинома с использованием коэффициентов (в степенной основе) начнет давать большие ошибки в плавающей запятой при высоких порядках. Предупреждение в документации Scipy пытается сказать вам это.

Вы должны использовать scipy.special.eval_genlaguerre(r_ord, phi_ord, float(x)) вместо genlaguerre + polyval; он использует более стабильный численный алгоритм для оценки полинома.

Источник

Вместо того, чтобы использовать scipy.special.eval_genlaguerre для оценки полинома высокой степени, как предложено pv, вы также можете использовать numpy.polynomial.Laguerre как объяснено в документации NumPy.

К сожалению, похоже, что она не обеспечивает функцию для обобщенных полиномов Лагерра.

import numpy as np
from numpy.polynomial import Laguerre
p = Laguerre([1, -2, 1])
x = np.arange(5)
p(x)

Выход NumPy: 0, 0,5, 2, 4,5, 8

Источник
Другие вопросы по тегам