Как выполнить *Fast* DCT (дискретное косинусное преобразование) в R?
Использование Rprof показало, что dct в пакете dtt является основным нарушителем кода R, который работал довольно медленно. Поменяв его на fft в пакете статистики (который не является тем же преобразованием, но должен вычисляться за то же время), моё время выполнения значительно улучшилось. На самом деле 2/3 моих Rprof-линий ранее были dct-вызовами, а всего лишь 3 из 600 строк были fft-вызовами после переключения.
Не реализована ли реализация dct в пакете dtt с использованием быстрого дискретного преобразования Фурье? Если это так, есть ли пакет, который есть? (Я знаю, что можно удвоить данные, а затем извлечь коэффициенты для dct из этих коэффициентов fft, но прямой быстрый dct наверняка будет лучше, и где-то действительно должен быть один).
3 ответа
Кажется, что нет быстрого dct, но в пакете статистики есть fft (быстрое преобразование Фурье), так что вот как можно получить быстрый dct с помощью fft.
Используйте это на свой страх и риск. Я не делал никаких серьезных проверок. Я проверил это на паре векторов разных размеров, и это дало те же результаты, что и функция dct в пакете dtt. Если кто-то захочет перепроверить меня, сравнив его с выводом dct, не стесняйтесь сделать это и опубликуйте свои результаты.
Возьмите ваш вектор и продлите его до вектора вдвое дольше, чем показано ниже: Если ваш вектор v=(1,2,3), то удвойте записи до w=(1,2,3,3,2,1). Обратите внимание на порядок. Если ваш вектор v=(1,2,4,9), то удвойте записи до w=(1,2,4,9,9,4,2,1)
Пусть N будет длиной вашего ОРИГИНАЛЬНОГО вектора (до того, как вы удвоите его длину).
Тогда первые N коэффициентов.5 * fft(w)/exp(complex(мнимый =pi / 2 / N)*(seq(2*N)-1)) должны согласовываться с вычислением dct(v), за исключением того, что значительно быстрее почти во всех случаях.
Скорость соображения. Если вы вычислите простой множитель N, тогда время, необходимое для вычисления быстрого dct, будет таким же, как время, необходимое для создания медленного dct для каждого из этих основных факторов. Таким образом, если N равно 2^K, это похоже на выполнение K различных медленных преобразований dct для вектора длины два, так что это действительно быстро. Если N простое (в худшем случае), то ускорение вообще не происходит. Наибольшее ускорение происходит на векторах, длина которых равна двум.
Примечание: приведенный выше код R выглядит невероятно недружелюбным, поэтому позвольте мне сказать, что происходит. После удвоения длины в правильном направлении, первые N коэффициентов БПФ, которые вы получите, почти правильные. Однако коэффициенты нужно немного подправить. Пусть P обозначает e^(pi * i / 2 / N). Оставьте первый коэффициент в покое. Разделите второй коэффициент на P, разделите третий на P^2, разделите четвертый на P^3 и т. Д. Затем разделите все коэффициенты на 2 (включая первый), чтобы согласиться с нормализацией R, используемой для dct,
Это должно дать то же самое, что и использование функции dct в пакете dtt, но значительно быстрее почти во всех случаях.
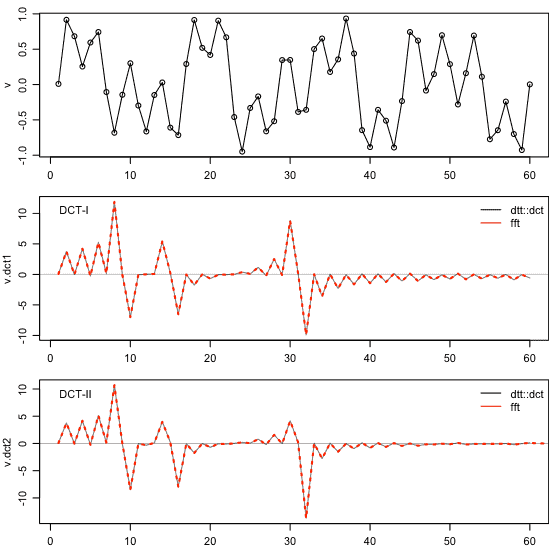
И Джон, и Игорь верны в своих ответах, но я подумал, что им не хватало примера кода.
library(dtt)
par(mfrow=c(3, 1), mar=c(2, 3, 1, 0.1), mgp=c(2, 0.8, 0))
set.seed(1)
N <- 60
v <- sin(seq(0, pi*2*4, l=N))/2 +
sin(seq(0, pi*2*7, l=N))/3 +
sin(seq(0, pi*2*15, l=N))/2 +
runif(N, -1, 1)/40 +
runif(N, -1, 1)/40
plot(v, type="o")
DCT-I:
v.dct1 <- dct(v, variant=1)
w <- c(v, v[(N - 1):2])
w.dct1 <- 0.5 * Re(fft(w)[1:N])
plot(v.dct1, type="l", col="#00000088")
abline(h=0, col="#00000044")
lines(w.dct1, col=2, lty=3, lwd=2)
legend("topright", c("dtt::dct", "fft"), bty="n", col=1:2, lwd=1)
legend("topleft", "DCT-I", bty="n")
DCT-II:
v.dct2 <- dct(v, variant=2)
P <- exp(complex(imaginary=pi / 2 / N)*(seq(2*N)-1))
w <- c(v, v[N:1])
w.dct2 <- 0.5 * Re(fft(w)[1:N]/P)
plot(v.dct2, type="l", col="#00000088")
abline(h=0, col="#00000044")
lines(w.dct2, col=2, lty=3, lwd=2)
legend("topright", c("dtt::dct", "fft"), bty="n", col=1:2, lwd=1)
legend("topleft", "DCT-II", bty="n")
Отказ от ответственности: я никогда не использовал dtt пакет и не могу сравнить мои результаты с его результатами. Мой ответ является общим в отношении DCT/FFT.
Идея Джона верна, но он двоякий в отношении повторения вектора и должен компенсировать его, подгоняя коэффициенты (e^(pi * i / 2 / N) фактор). При правильном расширении исходного вектора БПФ дает прямо правильные результаты (*). Цитировать из Википедии:
" DCT-I в точности эквивалентен (до общего масштабного коэффициента 2) DFT из 2N-2 действительных чисел с четной симметрией. Например, DCT-I из N=5 действительных чисел abcde в точности эквивалентен ДПФ из восьми действительных чисел abcdedcb (четная симметрия), разделенных на два. "
Т.е. если у нас есть вектор v = [1, 2, 3, 4, 5] на котором мы хотим выполнить DCT, мы должны построить новый вектор w = [1, 2, 3, 4, 5, 4, 3, 2] и выполнить БПФ на нем. Обратите внимание, что первый и последний компонент v появляются только один раз в w, в оригинальном порядке!
Это работает, потому что преобразование Фурье четной функции (функция, симметричная относительно нуля) состоит исключительно из вещественных (косинусных) коэффициентов. Если бы мы построили вектор w в том числе весь перевернутый v Джон предположил, что это будет симметрично -0.5, Из-за этого крошечного сдвига преобразование Фурье также будет генерировать мнимые (синусоидальные) коэффициенты.
(*) Метод здесь производит DCT-I. Метод Джона, похоже, нацелен на DCT-II.