Обратная функция заданной функции
У меня есть функция с двумя входами x а также y который возвращается z основанный на некоторых условиях (которые основаны на значениях x а также y). Нечто похожее на следующий псевдокод.
f(x, y)
if x < a && y < b
return z=x+y;
else if x >= a && x < c && y >= b && y < d
return z=x-y;
else x >= c && y >= d
return z=x*y;
Теперь я хочу написать функцию, которая почти действует как обратная функция для f (Давайте назовем это g). Псевдокод должен выглядеть примерно так:
g(z)
return x1, x2, y1 and y2; //x's, y's are corresponding boundaries for given z
Предположим, что f является очень очень простым и основывается только на нескольких условиях, а возвращаемое значение так же просто, как некоторые арифметические утверждения (в точности аналогичные приведенным выше). Как ты пишешь g? Вы просто храните границы и соответствующие возвращаемые значения из f а затем пройти между ними с заданным z найти подходящие границы? Я пытаюсь увидеть, как другие люди взломают это. Обратите внимание, что f также написано вами, и вы знаете все об этом.
ПРИМЕЧАНИЕ. Предположим, что возвращаемые значения всегда различны и не перекрываются ни в каких ситуациях.
2 ответа
Вы бы начали с рассмотрения каждого из условий. Каковы значения х и у, если они должны были соответствовать минимальному условию. Например, если x и y были чуть меньше, чем a и b соответственно, сможет ли уравнение x + y когда-либо удовлетворить z. То есть x + y будет больше, чем z. Если нет, то ни одно из чисел, меньших, чем текущие x и y, не может быть исключено. Затем вы можете перейти к следующему состоянию и так далее. Если значения для x и y могут удовлетворять условию, то вы должны начать с нижних границ и перебрать возможные значения в этом диапазоне или, возможно, использовать алгебру для ее решения.
ваша функция
double f(double x,double y) // z=f(x,y) { if ((x<a)&&(y<b)) return x+y; else if ((x>=a)&&(x<c)&&(y>=b)&&(y<d)) return x-y; else if ((x>=c)&&(y>=d)) return x*y; return ???; }если вам не хватает воображения, как я, то для лучшего понимания нарисуйте карту
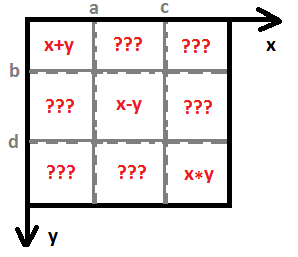
теперь более очевидно, что это отображение один ко многим
z=x+y -> y=z-x , x=z-y z=x-y -> y=x-z , x=z+y z=x*y -> y=z/x , x=z/yтакже эти 3 определенных интервала
x,yможет дать то же самоеzценностиобратная функция
не стоит возвращать интервалы
x,yлибо вы делаетеg()2D- функция, такая какx=g2d(y,z)или жеy=g2d(x,z),Или вы возвращаете список всех действительных
x,yпары не интервалы!!! Что также можно сделать через 2Dg()функцияпример 2D
gфункция:double g2d(double x,double z) // y=g(x,z) { if (x<a) return z-x; else if (x<c) return x-z; else return z/x; }Вы должны добавить также вычисляется
yпроверка диапазона для правильного решения перед возвратом, но я слишком ленив для этого.пример 1D
gфункция:void g(double *x,double *y,int &n,double z) // x[n],y[n]=g(z) ... x,y should be allocated big enough or use some list/vector template { double xx; const double min =-1e+3; const double max =+1e+3; const double step=+1e-3; n=0; // reset found solution count for (xx=min;xx<=max;xx+=step) // go through valid x axis { x[n]=xx; y[n]=g2d(xx,z); // here add check if solution valid and continue if not // also can add check for max n to avoid overrun of arrays x[],y[] n++; // add new valid solution to list } }
[заметки]
весь код в C++