Распознавание контуров 2D фигур

Я ищу, чтобы реализовать распознавание формы / сопоставление аналогичных кривых (дискретные точечные массивы) в 2D.

Я нашел статью на эту тему, но я немного растерялся, когда дело доходит до реализации этого в коде.

Я понял, что эту функцию нужно свернуть:

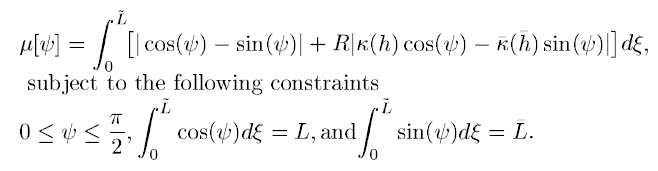
Но с чего мне начать?

  1. Кажется, μ - это измерение искажения, которое я хочу минимизировать.
  2. ψ кажется некоторым аргументом, который ограничен от 0 до π / 2
  3. "R - это параметр", что означает?
  4. κ это кривизна,?
  5. ξ - еще один параметр...
  6. gahhh

Кто-нибудь может, пожалуйста, наметить подход к этому на английском языке? А может быть, в каком-то псевдокоде?

Источник

2 ответа

Решение

Я думаю, что маловероятно, что вы сможете заставить это работать без понимания математики, и способ понять математику - это проработать статью с самого начала; если вы переходите к последнему уравнению и пытаетесь его закодировать, естественно, это не имеет смысла. Вот ответы на ваши конкретные вопросы, для чего они стоят:

  1. μ действительно является "измерением искажения" или стоимостью деформации одной кривой в другую.
  2. indeed действительно ограничено [0 и π/2]. Это угол кривой (h,h-bar) (извините, я не знаю, как вводить специальные символы).
  3. "R - это параметр", что означает, что он произвольный, мера того, насколько важна ориентация относительно перемещения.
  4. κ - кривизна, C - первая кривая.
  5. ξ - параметр, описывающий продвижение по обеим кривым. По мере продвижения ξ от 0 до L-тильды h(ξ) переходит от 0 до L, а h-bar(ξ) - от 0 до L-bar.
Источник

Мы начнем с некоторых определений:

  • Кривизна - это то, насколько кривая отклоняется от плоской.
  • Параметр определяет, какую кривую вы ищете. Например, f(x) = kx + m, k и m - параметры.

Что касается минимизации, вы можете посмотреть здесь: http://en.wikipedia.org/wiki/Calculus_of_variations

Источник
Другие вопросы по тегам