Что такое экзистенциальный тип?

Question

Я прочитал в Википедии статью Экзистенциальные типы. Я понял, что они называются экзистенциальными типами из-за экзистенциального оператора (∃). Я не уверен, какой в ​​этом смысл. В чем разница между

T = ∃X { X a; int f(X); }

а также

T = ∀x { X a; int f(X); }

?

Answer 1

Когда кто-то определяет универсальный тип ∀X они говорят: вы можете подключить любой тип, который вы хотите, мне не нужно ничего знать о типе, чтобы выполнять свою работу, я буду называть его только непрозрачным X,

Когда кто-то определяет экзистенциальный тип ∃X они говорят: я буду использовать любой тип, который я хочу здесь; Вы ничего не знаете о типе, поэтому можете ссылаться на него только как непрозрачный. X,

Универсальные типы позволяют писать такие вещи, как:

void copy<T>(List<T> source, List<T> dest) {
   ...
}

copy функция понятия не имеет, что T будет на самом деле, но это не нужно.

Экзистенциальные типы позволят вам написать такие вещи, как:

interface VirtualMachine<B> {
   B compile(String source);
   void run(B bytecode);
}

// Now, if you had a list of VMs you wanted to run on the same input:
void runAllCompilers(List<∃B:VirtualMachine<B>> vms, String source) {
   for (∃B:VirtualMachine<B> vm : vms) {
      B bytecode = vm.compile(source);
      vm.run(bytecode);
   }
}

Каждая реализация виртуальной машины в списке может иметь свой тип байт-кода. runAllCompilers функция не имеет представления о типе байт-кода, но в этом нет необходимости; все, что он делает, это передает байт-код от VirtualMachine.compile в VirtualMachine.run,

Подстановочные знаки типа Java (например: List<?>) очень ограниченная форма экзистенциальных типов.

Обновление: забыл упомянуть, что вы можете сортировать экзистенциальные типы с помощью универсальных типов. Во-первых, оберните ваш универсальный тип, чтобы скрыть параметр типа. Во-вторых, инвертированный контроль (это эффективно меняет часть "ты" и "я" в вышеприведенных определениях, что является основным различием между экзистенциалами и универсалиями).

// A wrapper that hides the type parameter 'B'
interface VMWrapper {
   void unwrap(VMHandler handler);
}

// A callback (control inversion)
interface VMHandler {
   <B> void handle(VirtualMachine<B> vm);
}

Теперь мы можем иметь VMWrapper позвоните нам VMHandler который имеет универсально типизированный handle функция. Чистый эффект тот же, наш код должен лечить B как непрозрачный.

void runWithAll(List<VMWrapper> vms, final String input)
{
   for (VMWrapper vm : vms) {
      vm.unwrap(new VMHandler() {
         public <B> void handle(VirtualMachine<B> vm) {
            B bytecode = vm.compile(input);
            vm.run(bytecode);
         }
      });
   }
}

Пример реализации ВМ:

class MyVM implements VirtualMachine<byte[]>, VMWrapper {
   public byte[] compile(String input) {
      return null; // TODO: somehow compile the input
   }
   public void run(byte[] bytecode) {
      // TODO: Somehow evaluate 'bytecode'
   }
   public void unwrap(VMHandler handler) {
      handler.handle(this);
   }
}

Answer 2

Значение экзистенциального типа, как ∃x. F(x) это пара, содержащая некоторый тип x и значение типа F(x), Принимая во внимание, что значение полиморфного типа, как ∀x. F(x) это функция, которая принимает некоторый тип x и выдает значение типа F(x), В обоих случаях тип закрывается над каким-то конструктором типа F,

Обратите внимание, что в этом представлении смешиваются типы и значения. Существующее доказательство - один тип и одно значение. Универсальное доказательство - это целое семейство значений, проиндексированных по типу (или отображение типов в значения).

Таким образом, разница между двумя указанными вами типами заключается в следующем:

T = ∃X { X a; int f(X); }

Это означает: значение типа T содержит тип с именем X, ценность a:X и функция f:X->int, Производитель значений типа T получает возможность выбрать любой тип для X и потребитель не может ничего знать о X, За исключением того, что есть один пример этого называется a и что это значение может быть превращено в int давая это f, Другими словами, значение типа T знает, как произвести int как-то. Ну, мы могли бы устранить промежуточный тип X и просто скажи:

T = int

Универсально выраженный немного отличается.

T = ∀X { X a; int f(X); }

Это означает: значение типа T можно дать любой тип X и это будет производить значение a:X и функция f:X->int не важно что X есть Другими словами: потребитель значений типа T можно выбрать любой тип для X, И производитель значений типа T ничего не могу знать о X, но он должен быть в состоянии произвести ценность a на любой выбор X и сможет превратить такую ​​ценность в int,

Очевидно, что реализация этого типа невозможна, потому что нет программы, которая могла бы создать значение каждого мыслимого типа. Если вы не допускаете такие нелепости, как null или днища.

Поскольку экзистенциальный является парой, экзистенциальный аргумент может быть преобразован в универсальный с помощью карри.

(∃b. F(b)) -> Int

такой же как:

∀b. (F(b) -> Int)

Первый является экзистенциальным ранга 2. Это приводит к следующему полезному свойству:

Каждый экзистенциально количественный тип ранга n+1 является универсально определенным типом ранга n,

Существует стандартный алгоритм превращения экзистенциалов в универсалии, называемый сколемизацией.

Answer 3

Я думаю, что имеет смысл объяснять экзистенциальные типы вместе с универсальными типами, поскольку эти два понятия дополняют друг друга, то есть одно является "противоположностью" другого.

Я не могу ответить на каждую деталь об экзистенциальных типах (таких как точное определение, список всех возможных применений, их связь с абстрактными типами данных и т. Д.), Потому что я просто недостаточно осведомлен для этого. Я продемонстрирую только (с использованием Java), что в этой статье на HaskellWiki говорится, что это основной эффект экзистенциальных типов:

Экзистенциальные типы могут использоваться для нескольких различных целей. Но то, что они делают, это "скрывают" переменную типа с правой стороны. Как правило, любая переменная типа, появляющаяся справа, также должна появляться слева […]

Пример установки:

Следующий псевдокод не совсем корректный Java, хотя это было бы достаточно легко исправить. На самом деле, это именно то, что я собираюсь сделать в этом ответе!

class Tree<α>
{
    α       value;
    Tree<α> left;
    Tree<α> right;
}

int height(Tree<α> t)
{
    return (t != null)  ?  1 + max( height(t.left), height(t.right) )
                        :  0;
}

Позвольте мне кратко изложить это для вас. Мы определяем...

• рекурсивный тип Tree<α> который представляет узел в двоичном дереве. Каждый узел хранит value некоторого типа α и имеет ссылки на необязательные left а также right поддеревья того же типа.

• функция height который возвращает самое дальнее расстояние от любого конечного узла до корневого узла t,

Теперь давайте обратимся к приведенному выше псевдокоду для height в правильный синтаксис Java! (Я буду продолжать опускать некоторые шаблоны для краткости, такие как модификаторы объектной ориентации и доступности.) Я собираюсь показать два возможных решения.

1. Универсальный тип решения:

Самое очевидное решение - просто сделать height универсальный, вводя параметр типа α в его сигнатуру:

<α> int height(Tree<α> t)
{
    return (t != null)  ?  1 + max( height(t.left), height(t.right) )
                        :  0;
}

Это позволит вам объявлять переменные и создавать выражения типа α внутри этой функции, если вы захотите. Но...

2. Экзистенциальное решение типа:

Если вы посмотрите на тело нашего метода, вы заметите, что мы на самом деле не обращаемся или не работаем с чем-либо типа α! Нет ни одного выражения, имеющего этот тип, ни переменных, объявленных с этим типом... так, почему мы должны сделать height универсальный вообще? Почему мы не можем просто забыть об α? Как оказалось, мы можем:

int height(Tree<?> t)
{
    return (t != null)  ?  1 + max( height(t.left), height(t.right) )
                        :  0;
}

Как я уже писал в самом начале этого ответа, экзистенциальные и универсальные типы имеют комплементарный / двойственный характер. Таким образом, если решение универсального типа было сделать height более универсальный, тогда мы должны ожидать, что экзистенциальные типы имеют противоположный эффект: делая его менее универсальным, а именно, скрывая / удаляя параметр типа α.

Как следствие, вы больше не можете ссылаться на тип t.value в этом методе не манипулируйте никакими выражениями этого типа, потому что ни один идентификатор не был привязан к нему. (The ? Подстановочный знак - это специальный токен, а не идентификатор, который "захватывает" тип.) t.value эффективно стал непрозрачным; возможно, единственное, что вы все еще можете сделать с ним, это набрать его Object,

Резюме:

===========================================================
                     |    universally       existentially
                     |  quantified type    quantified type
---------------------+-------------------------------------
 calling method      |                  
 needs to know       |        yes                no
 the type argument   |                 
---------------------+-------------------------------------
 called method       |                  
 can use / refer to  |        yes                no  
 the type argument   |                  
=====================+=====================================

Answer 4

Все это хорошие примеры, но я решил ответить на это немного по-другому. Напомним из математики, что ∀x. P(x) означает "для всех x, я могу доказать, что P(x)". Другими словами, это своего рода функция, вы даете мне крестик, и у меня есть метод, чтобы доказать это для вас.

В теории типов мы говорим не о доказательствах, а о типах. Таким образом, в этом пространстве мы имеем в виду "для любого типа X, который вы мне дадите, я дам вам конкретный тип P". Теперь, поскольку мы не даем P много информации о X, кроме того, что это тип, P не может ничего с этим поделать, но есть несколько примеров. P может создать тип "все пары одного типа": P<X> = Pair<X, X> = (X, X), Или мы можем создать тип опции: P<X> = Option<X> = X | Nilгде Nil - это тип нулевых указателей. Мы можем сделать список из этого: List<X> = (X, List<X>) | Nil, Обратите внимание, что последний является рекурсивным, значения List<X> либо пары, где первый элемент является X, а второй элемент является List<X> или это нулевой указатель.

Теперь в математике ∃x. P(x) означает "Я могу доказать, что существует конкретный x такой, что P (x) верен". Таких х может быть много, но для доказательства достаточно одного. Другой способ думать об этом состоит в том, что должен существовать непустой набор пар доказательство-доказательство {(x, P(x))}.

Переведено в теорию типов: тип в семье ∃X.P<X> это тип X и соответствующий тип P<X>, Обратите внимание на то, что до того, как мы передали X Р, (чтобы мы знали все о Х, но Р очень мало), теперь все наоборот. P<X> не обещает давать какую-либо информацию о X, только то, что там есть один, и что это действительно тип.

Чем это полезно? Ну, P может быть типом, который имеет способ раскрытия своего внутреннего типа X. Примером может быть объект, который скрывает внутреннее представление своего состояния X. Хотя у нас нет никакого способа непосредственно манипулировать им, мы можем наблюдать его эффект, poking at P. Может быть много реализаций этого типа, но вы можете использовать все эти типы независимо от того, какой из них был выбран.

Answer 5

Чтобы прямо ответить на ваш вопрос:

С универсальным типом, использует T должен включать параметр типа X, Например T<String> или же T<Integer>, Для экзистенциального типа используется T не включайте этот параметр типа, потому что он неизвестен или не имеет значения - просто используйте T (или на Java T<?>).

Дальнейшая информация:

Универсальные / абстрактные типы и экзистенциальные типы - это двойственная перспектива между потребителем / клиентом объекта / функции и производителем / реализацией этого. Когда одна сторона видит универсальный тип, другая видит экзистенциальный тип.

В Java вы можете определить универсальный класс:

public class MyClass<T> {
   // T is existential in here
   T whatever; 
   public MyClass(T w) { this.whatever = w; }

   public static MyClass<?> secretMessage() { return new MyClass("bazzlebleeb"); }
}

// T is universal from out here
MyClass<String> mc1 = new MyClass("foo");
MyClass<Integer> mc2 = new MyClass(123);
MyClass<?> mc3 = MyClass.secretMessage();

• С точки зрения клиента MyClass, T универсален, потому что вы можете заменить любой тип T когда вы используете этот класс, и вы должны знать фактический тип T всякий раз, когда вы используете экземпляр MyClass
• С точки зрения методов экземпляра в MyClass сам, T является экзистенциальным, потому что он не знает реальный тип T
• В Java ? представляет экзистенциальный тип - таким образом, когда вы находитесь внутри класса, T в основном ?, Если вы хотите обработать экземпляр MyClass с T экзистенциально, вы можете объявить MyClass<?> как в secretMessage() пример выше.

Экзистенциальные типы иногда используются, чтобы скрыть детали реализации чего-либо, как обсуждалось в другом месте. Java-версия этого может выглядеть так:

public class ToDraw<T> {
    T obj;
    Function<Pair<T,Graphics>, Void> draw;
    ToDraw(T obj, Function<Pair<T,Graphics>, Void>
    static void draw(ToDraw<?> d, Graphics g) { d.draw.apply(new Pair(d.obj, g)); }
}

// Now you can put these in a list and draw them like so:
List<ToDraw<?>> drawList = ... ;
for(td in drawList) ToDraw.draw(td);

Немного сложно понять это правильно, потому что я притворяюсь, что я использую какой-то функциональный язык программирования, а не Java. Но суть в том, что вы фиксируете какое-то состояние и список функций, которые работают с этим состоянием, и вы не знаете реальный тип части состояния, но функции знают, так как они уже сопоставлены с этим типом.,

Теперь в Java все не финальные не примитивные типы являются частично экзистенциальными. Это может звучать странно, но потому что переменная объявлена ​​как Object потенциально может быть подклассом Object вместо этого вы не можете объявить определенный тип, только "этот тип или подкласс". И так, объекты представлены как бит состояния плюс список функций, которые работают с этим состоянием - какая именно функция вызывается, определяется во время выполнения поиском. Это очень похоже на использование экзистенциальных типов выше, где у вас есть часть экзистенциального состояния и функция, которая работает с этим состоянием.

В статически типизированных языках программирования без подтипов и приведений экзистенциальные типы позволяют управлять списками объектов различного типа. Список T<Int> не может содержать T<Long>, Тем не менее, список T<?> может содержать любое изменение Tпозволяя помещать в список множество различных типов данных и преобразовывать их все в целое число (или делать любые операции, предусмотренные в структуре данных) по требованию.

Можно в значительной степени всегда конвертировать запись с экзистенциальным типом в запись без использования замыканий. Закрытие также типизировано экзистенциально, поскольку свободные переменные, по которым оно закрыто, скрыты от вызывающей стороны. Таким образом, язык, который поддерживает замыкания, но не экзистенциальные типы, может позволить вам создавать замыкания, которые имеют то же скрытое состояние, которое вы бы поместили в экзистенциальную часть объекта.

Answer 6

Экзистенциальный тип - это непрозрачный тип.

Подумайте о дескрипторе файла в Unix. Вы знаете, что его тип int, так что вы можете легко подделать его. Например, вы можете попробовать прочитать из дескриптора 43. Если так получилось, что в программе есть файл, открытый с помощью этого конкретного дескриптора, вы будете читать из него. Ваш код не должен быть вредоносным, просто небрежным (например, дескриптор может быть неинициализированной переменной).

Экзистенциальный тип скрыт от вашей программы. Если fopen возвратил экзистенциальный тип, все, что вы можете с ним сделать - это использовать его с некоторыми библиотечными функциями, которые принимают этот экзистенциальный тип. Например, следующий псевдокод будет компилироваться:

let exfile = fopen("foo.txt"); // No type for exfile!
read(exfile, buf, size);

Интерфейс "чтение" объявлен как:

Существует тип T такой, что:

size_t read(T exfile, char* buf, size_t size);

Переменная exfile не является int, не char*а не struct File - ничего, что вы можете выразить в системе типов. Вы не можете объявить переменную, тип которой неизвестен, и вы не можете привести, скажем, указатель к этому неизвестному типу. Язык не позволит вам.

Answer 7

Кажется, я опаздываю, но в любом случае, этот документ добавляет другое представление о том, что такое экзистенциальные типы, хотя они не являются специфически независимыми от языка, тогда должно быть довольно легко понять экзистенциальные типы: http://www.cs.uu.nl/groups/ST/Projects/ehc/ehc-book.pdf (глава 8)

Различие между универсально и экзистенциально количественным типом может быть охарактеризовано следующим наблюдением:

• Использование значения с квантифицированным типом определяет тип, который нужно выбрать для создания экземпляра квантифицированной переменной типа. Например, вызывающая функция идентификатора "id:: aaa → a" определяет тип, который нужно выбрать для переменной типа a для этого конкретного применения id. Для приложения функции "id 3" этот тип равен Int.

• Создание значения с квантифицированным типом определяет и скрывает тип переменной квантифицированного типа. Например, создатель ".a.(A, a → Int)" мог построить значение этого типа из "(3, λx → x)"; другой создатель построил значение с таким же типом из "(" x ", λx → ord x)". С точки зрения пользователя оба значения имеют одинаковый тип и, таким образом, являются взаимозаменяемыми. У значения есть определенный тип, выбранный для переменной типа a, но мы не знаем, какой тип, поэтому эта информация больше не может быть использована. Это значение конкретного типа информации было "забыто"; мы только знаем, что это существует.

Answer 8

Универсальный тип существует для всех значений параметра (ов) типа. Экзистенциальный тип существует только для значений параметра (ов) типа, которые удовлетворяют ограничениям экзистенциального типа.

Например, в Scala одним из способов выражения экзистенциального типа является абстрактный тип, который ограничен некоторыми верхними или нижними границами.

trait Existential {
  type Parameter <: Interface
}

Эквивалентно ограниченный универсальный тип - это экзистенциальный тип, как в следующем примере.

trait Existential[Parameter <: Interface]

Любое использование сайта может использовать Interface потому что любые инстанцируемые подтипы Existential должен определить type Parameter который должен реализовать Interface,

Вырожденный случай экзистенциального типа в Scala является абстрактным типом, на который никогда не ссылаются, и, таким образом, его не нужно определять каким-либо подтипом. Это эффективно имеет сокращенную запись List[_] в Скале и List<?> на Яве.

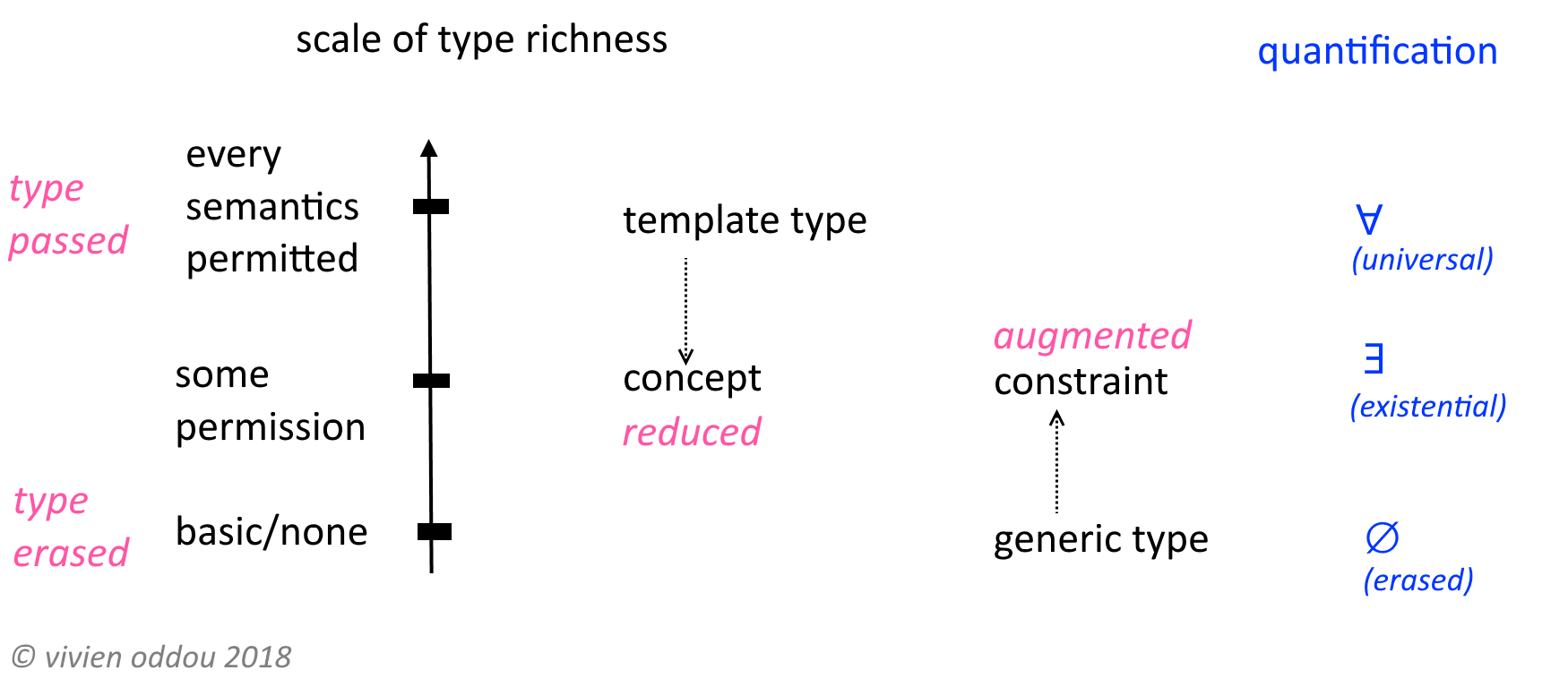
Мой ответ был вдохновлен предложением Мартина Одерского объединить абстрактные и экзистенциальные типы. Прилагаемый слайд помогает понять.

Answer 9

Исследования абстрактных типов данных и сокрытия информации привели экзистенциальные типы в языки программирования. Создание абстрактного типа данных скрывает информацию об этом типе, поэтому клиент этого типа не может злоупотреблять им. Скажем, у вас есть ссылка на объект... некоторые языки позволяют вам преобразовывать эту ссылку в ссылку на байты и делать все, что вы хотите, с этим фрагментом памяти. В целях гарантии поведения программы для языка полезно обеспечить, чтобы вы действовали только в отношении ссылки на объект с помощью методов, предоставляемых конструктором объекта. Вы знаете, что тип существует, но не более того.

Увидеть:

Абстрактные типы имеют экзистенциальный тип, MITCHEL & PLOTKIN

http://theory.stanford.edu/~jcm/papers/mitch-plotkin-88.pdf

Answer 10

Я создал эту диаграмму. Я не знаю, строго ли это. Но если это поможет, я рад.

Answer 11

Как я понимаю, это математический способ описания интерфейсов / абстрактного класса.

Что касается T = ∃X { X a; int f(X); }

Для C# это будет переводиться в общий абстрактный тип:

abstract class MyType<T>{
    private T a;

    public abstract int f(T x);
}

"Экзистенциальный" просто означает, что существует некоторый тип, который подчиняется правилам, определенным здесь.