Обработка ограничений Prolog: Упаковочные квадраты
Я пытаюсь решить проблему обработки ограничений в прологе.
Мне нужно упаковать 4 квадрата 5x5,4x4,3x3 и 2x2 в сетке 10x10. Они не могут пересекаться.
Мои переменные выглядят так:
Name: SqX(i), i=1..10, domain: 1..10
Где X 5,4,3 или 2. Индекс i представляет строку, домен - столбец в сетке.
Мои первые ограничения пытаются определить ширину и высоту квадратов. Я формулирую это так:
Constraint: SqX(i) > SqX(j)-X /\ i>j-X, range: i>0 /\ j>0
Так что возможные точки ограничены, чтобы быть в пределах X строк и столбцов друг от друга. Пролог, однако, останавливается на этих ограничениях и дает следующий результат:
Adding constraint "(Sq5_I > Sq5_J-5) /\ (I>J-5)" for values:
I=1, J=1,
I=1, J=2,
I=1, J=3,
I=1, J=4,
I=1, J=5,
I=1, J=6,
=======================[ End Solutions ]=======================
Так что это останавливается там, даже не проверяя другие квадраты. Мои ограничения, скорее всего, слишком жесткие, но я не понимаю, почему и как. Какие-либо предложения?
4 ответа
Для каждого квадрата определите X а также Y переменные, которые обозначают верхний левый угол. Эти переменные будут иметь домены 1..10-L, где L это длина квадрата. Если вы установите домен в 1..10квадраты могут быть размещены частично за пределами вашего прямоугольника 10х10.
Затем вы можете разместить ограничения для каждой пары прямоугольников (X,Y) а также (X1,Y1) это означает, что если они перекрываются по оси x, они не должны перекрываться по оси y, и наоборот:
(((X #=< X1) and (X+L #> X1)) => ((Y+L #=< Y1) or (Y1+L1 #=< Y))),
(((X1 #=< X) and (X1+L1 #> X)) => ((Y+L #=< Y1) or (Y1+L1 #=< Y))),
(((Y #=< Y1) and (Y+L #> Y1)) => ((X+L #=< X1) or (X1+L1 #=< X))),
(((Y1 #=< Y) and (Y1+L1 #> Y)) => ((X+L #=< X1) or (X1+L1 #=< X)))
(ваш конкретный синтаксис ограничений может отличаться)
Начиная с версии 3.8.3, SICStus Prolog предлагает ряд специальных ограничений размещения, которые хорошо соответствуют вашей проблеме с упаковкой. В частности, поскольку ваша проблема упаковки является двумерной, вы должны рассмотреть возможность использования disjoint2/1 ограничение.
Следующий фрагмент кода использует disjoint2/1 чтобы выразить, что прямоугольники не перекрываются. Основное отношение area_boxes_positions_/4,
:- use_module(library(clpfd)).
:- use_module(library(lists)).
area_box_pos_combined(W_total*H_total,W*H,X+Y,f(X,W,Y,H)) :-
X #>= 1,
X #=< W_total-W+1,
Y #>= 1,
Y #=< H_total-H+1.
positions_vars([],[]).
positions_vars([X+Y|XYs],[X,Y|Zs]) :-
positions_vars(XYs,Zs).
area_boxes_positions_(Area,Bs,Ps,Zs) :-
maplist(area_box_pos_combined(Area),Bs,Ps,Cs),
disjoint2(Cs),
positions_vars(Ps,Zs).
На некоторые вопросы! Во-первых, ваша первоначальная проблема с упаковкой:
?- area_boxes_positions_(10*10,[5*5,4*4,3*3,2*2],Positions,Zs),
labeling([],Zs).
Positions = [1+1,1+6,5+6,5+9],
Zs = [1,1,1,6,5,6,5,9] ? ...
Далее давайте минимизируем общую площадь, необходимую для размещения всех квадратов:
?- domain([W,H],1,10),
area_boxes_positions_(W*H,[5*5,4*4,3*3,2*2],Positions,Zs),
WH #= W*H,
minimize(labeling([ff],[H,W|Zs]),WH).
W = 9,
H = 7,
Positions = [1+1,6+1,6+5,1+6],
Zs = [1,1,6,1,6,5,1,6],
WH = 63 ? ...
Визуализирующие решения
Как на самом деле выглядят индивидуальные решения? ImageMagick может создавать хорошие маленькие растровые изображения...
Вот некоторый быстрый и грязный код для вывода правильной команды ImageMagick:
:- use_module(library(between)).
:- use_module(library(codesio)).
drawWithIM_at_area_name_label(Sizes,Positions,W*H,Name,Label) :-
Pix = 20,
% let the ImageMagick command string begin
format('convert -size ~dx~d xc:skyblue', [(W+2)*Pix, (H+2)*Pix]),
% fill canvas
format(' -stroke none -draw "fill darkgrey rectangle ~d,~d ~d,~d"',
[Pix,Pix, (W+1)*Pix-1,(H+1)*Pix-1]),
% draw grid
drawGridWithIM_area_pix("stroke-dasharray 1 1",W*H,Pix),
% draw boxes
drawBoxesWithIM_at_pix(Sizes,Positions,Pix),
% print label
write( ' -stroke none -fill black'),
write( ' -gravity southwest -pointsize 16 -annotate +4+0'),
format(' "~s"',[Label]),
% specify filename
format(' ~s~n',[Name]).
Выше код для drawWithIM_at_area_name_label/5 опирается на двух маленьких помощников:
drawGridWithIM_area_pix(Stroke,W*H,P) :- % vertical lines
write(' -strokewidth 1 -fill none -stroke gray'),
between(2,W,X),
format(' -draw "~s path \'M ~d,~d L ~d,~d\'"', [Stroke,X*P,P, X*P,(H+1)*P-1]),
false.
drawGridWithIM_area_pix(Stroke,W*H,P) :- % horizontal lines
between(2,H,Y),
format(' -draw "~s path \'M ~d,~d L ~d,~d\'"', [Stroke,P,Y*P, (W+1)*P-1,Y*P]),
false.
drawGridWithIM_area_pix(_,_,_).
drawBoxesWithIM_at_pix(Sizes,Positions,P) :-
Colors = ["#ff0000","#00ff00","#0000ff","#ffff00","#ff00ff","#00ffff"],
write(' -strokewidth 2 -stroke white'),
nth1(N,Positions,Xb+Yb),
nth1(N,Sizes, Wb*Hb),
nth1(N,Colors, Color),
format(' -draw "fill ~sb0 roundrectangle ~d,~d ~d,~d ~d,~d"',
[Color, Xb*P+3,Yb*P+3, (Xb+Wb)*P-3,(Yb+Hb)*P-3, P/2,P/2]),
false.
drawBoxesWithIM_at_pix(_,_,_).
Использование визуализаторов
Давайте использовать следующие два запроса для создания некоторых неподвижных изображений.
?- drawWithIM_at_area_name_label([5*5,4*4,3*3,2*2],[1+1,6+1,6+5,1+6],9*7,
'dj2_9x7.gif','9x7').
?- drawWithIM_at_area_name_label([5*5,4*4,3*3,2*2],[1+1,1+6,5+6,5+9],10*10,
'dj2_10x10.gif','10x10').
Давайте используем следующий хак-запрос для создания изображения для каждого решения размещения вышеупомянутых прямоугольников на доске размера 9*7:
?- retractall(nSols(_)),
assert(nSols(1)),
W=9,H=7,
Boxes = [5*5,4*4,3*3,2*2],
area_boxes_positions_(W*H,Boxes,Positions,Zs),
labeling([],Zs),
nSols(N),
retract(nSols(_)),
format_to_codes('dj2_~5d.gif',[N],Name),
format_to_codes('~dx~d: solution #~d',[W,H,N],Label),
drawWithIM_at_area_name_label(Boxes,Positions,W*H,Name,Label),
N1 is N+1,
assert(nSols(N1)),
false.
Затем выполните все команды ImageMagick, полученные по указанным выше запросам.
Наконец, создайте анимацию набора решений третьего запроса, используя ImageMagick:
$ convert -delay 15 dj2_0.*.gif dj2_9x7_allSolutions_1way.gif
$ convert dj2_9x7_allSolutions_1way.gif -coalesce -duplicate 1,-2-1 \
-quiet -layers OptimizePlus -loop 0 dj2_9x7_allSolutions.gif
Результаты
Во-первых, одно решение для платы размером 10*10: 
Во-вторых, одно решение для доски минимального размера (9*7): 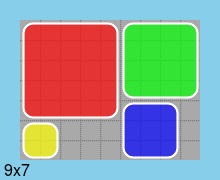
Наконец, все решения для доски минимального размера (9*7): 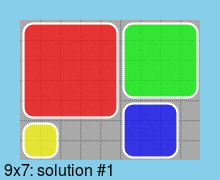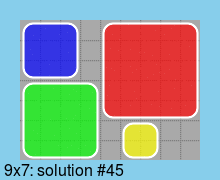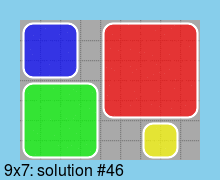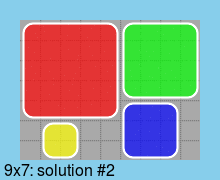
Редактировать 2015-04-14
Начиная с версии 7.1.36 библиотека clpfd SWI-Prolog поддерживает ограничение disjoint2/1,
Редактировать 2015-04-22
Вот эскиз альтернативной реализации, основанной на tuples_in/2 ограничение:
- Для каждой пары ящиков определите все позиции, в которых эти два элемента не будут перекрываться.
- Закодируйте действительные комбинации в виде списков кортежей.
- По каждой паре коробок оставьте по одному
tuples_in/2ограничение.
Как личное доказательство концепции, я реализовал некоторый код, следуя этой идее; как @CapelliC в своем ответе, я получаю 169480 отличные решения для коробок и размеров платы, заявленной OP.
Время выполнения сопоставимо с другими ответами на основе clp(FD); на самом деле он очень конкурентоспособен для небольших плат (10*10 и меньше), но становится намного хуже с большими размерами плат.
Пожалуйста, признайте, что ради приличия я воздерживаюсь от публикации кода:)
Здесь уже опубликовано несколько отличных решений (+1 для всех!) С использованием ограничений CLP(FD).
Кроме того, я хотел бы показать один концептуально иной способ решения таких задач размещения и покрытия с использованием ограничений CLP (B).
Идея состоит в том, чтобы рассматривать каждое возможное размещение тайла как набор значений TRUE в определенных элементах сетки, где каждый элемент сетки соответствует одному столбцу матрицы, а каждое возможное размещение тайла соответствует одной строке. Задача состоит в том, чтобы затем выбрать набор строк указанной матрицы таким образом, чтобы каждый элемент сетки покрывался не более одного раза, или, другими словами, в каждом столбце подматрицы, состоящей из выбранных строк, имеется не более одного значения TRUE.,
В этой формулировке выбор строк - и, следовательно, размещение плиток в определенных позициях - указывается логическими переменными, по одной на каждую строку матрицы.
Вот код, которым я хотел бы поделиться, он работает в SICStus Prolog и SWI при минимальных изменениях:
:- use_module(library(clpb)).
:- use_module(library(clpfd)).
/* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The tiles we have available for placement.
For example, a 2x2 tile is represented in matrix form as:
[[1,1],
[1,1]]
1 indicates which grid elements are covered when placing the tile.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
tile(5*5).
tile(4*4).
tile(3*3).
tile(2*2).
tile_matrix(Rows) :-
tile(M*N),
length(Rows, M),
maplist(length_list(N), Rows),
append(Rows, Ls),
maplist(=(1), Ls).
length_list(L, Ls) :- length(Ls, L).
/* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Describe placement of tiles as SAT constraints.
Notice the use of Cards1 to make sure that each tile is used
exactly once. Remove or change this constraint if a shape can be
used multiple times, or can even be omitted.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
placement(M, N, Vs, *(Cs) * *(Cards1)) :-
matrix(M, N, TilesRows),
pairs_keys_values(TilesRows, Tiles, Rows),
same_length(Rows, Vs),
pairs_keys_values(TilesVs0, Tiles, Vs),
keysort(TilesVs0, TilesVs),
group_pairs_by_key(TilesVs, Groups),
pairs_values(Groups, SameTiles),
maplist(card1, SameTiles, Cards1),
Rows = [First|_],
phrase(all_cardinalities(First, Vs, Rows), Cs).
card1(Vs, card([1], Vs)).
all_cardinalities([], _, _) --> [].
all_cardinalities([_|Rest], Vs, Rows0) -->
{ maplist(list_first_rest, Rows0, Fs, Rows),
pairs_keys_values(Pairs0, Fs, Vs),
include(key_one, Pairs0, Pairs),
pairs_values(Pairs, Cs) },
[card([0,1], Cs)],
all_cardinalities(Rest, Vs, Rows).
key_one(1-_).
list_first_rest([L|Ls], L, Ls).
/* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
We build a matrix M_ij, where each row i describes what placing a
tile at a specific position looks like: Each cell of the grid
corresponds to a unique column of the matrix, and the matrix
entries that are 1 indicate the grid positions that are covered by
placing one of the tiles at the described position. Therefore,
placing all tiles corresponds to selecting specific rows of the
matrix such that, for the selected rows, at most one "1" occurs in
each column.
We represent each row of the matrix as Ts-Ls, where Ts is the tile
that is used in each case.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
matrix(M, N, Ms) :-
Squares #= M*N,
length(Ls, Squares),
findall(Ts-Ls, line(N, Ts, Ls), Ms).
line(N, Ts, Ls) :-
tile_matrix(Ts),
length(Ls, Max),
phrase((zeros(0,P0),tile_(Ts,N,Max,P0,P1),zeros(P1,_)), Ls).
tile_([], _, _, P, P) --> [].
tile_([T|Ts], N, Max, P0, P) -->
tile_part(T, N, P0, P1),
{ (P1 - 1) mod N >= P0 mod N,
P2 #= min(P0 + N, Max) },
zeros(P1, P2),
tile_(Ts, N, Max, P2, P).
tile_part([], _, P, P) --> [].
tile_part([L|Ls], N, P0, P) --> [L],
{ P1 #= P0 + 1 },
tile_part(Ls, N, P1, P).
zeros(P, P) --> [].
zeros(P0, P) --> [0], { P1 #= P0 + 1 }, zeros(P1, P).
Следующий запрос показывает, какие элементы сетки покрыты (1), где каждая строка соответствует расположению одного из прямоугольников:
?- M = 7, N = 9, placement(M, N, Vs, Sat), sat(Sat),
labeling(Vs), matrix(M, N, Ms), pairs_values(Ms, Rows),
pairs_keys_values(Pairs0, Vs, Rows),
include(key_one, Pairs0, Pairs1), pairs_values(Pairs1, Covers),
maplist(writeln, Covers).
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,0,0,0,0]
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,1,1,1,1,0,0,0,0,0,1,1,1,1,0,0,0,0,0,1,1,1,1]
[0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
[0,0,0,0,1,1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
M = 7,
N = 9,
etc.
в соответствии с решением:
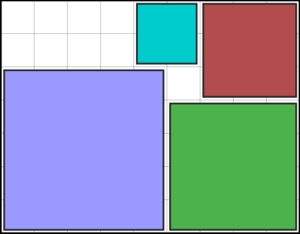
Такая формулировка CLP(B) обычно менее масштабируема, чем версия CLP(FD), также потому, что в нее вовлечено больше переменных. Тем не менее, он также имеет несколько преимуществ:
Одним значительным преимуществом является то, что он легко обобщается на вариант задачи, в котором некоторые или все формы могут использоваться несколько раз. Например, в версии выше, мы можем просто изменить card1/2 чтобы:
custom_cardinality(Vs, card([0,1,2,3,4,5,6,7], Vs)).
и получить версию, в которой каждую плитку можно использовать до 7 раз, и даже можно полностью ее исключить (из-за включения 0).
Во-вторых, мы можем легко превратить это в решение для точной задачи покрытия, что означает, что каждый элемент сетки покрывается одной из фигур, путем простого изменения card([0,1], Cs) в card([1], Cs) в all_cardinalities//3,
Вместе с другой модификацией, здесь есть покрытие для сетки 4x4 с использованием четырех прямоугольников 2x2:
[1,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0]
[0,0,1,1,0,0,1,1,0,0,0,0,0,0,0,0]
[0,0,0,0,0,0,0,0,1,1,0,0,1,1,0,0]
[0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,1]
Третье преимущество формулировки CLP(B) состоит в том, что число решений может быть вычислено без явного перечисления решений. Например, для исходного задания:
?- placement(7, 9, Vs, Sat), sat_count(Sat, Count).
Count = 68.
Эти 68 решений прекрасно иллюстрируются @repeat.
Для сравнения приведено количество решений, в которых каждую фигуру можно использовать от 0 до 7 раз:
?- placement(7, 9, Vs, Sat), time(sat_count(Sat, Count)).
% 157,970,727 inferences, 19.165 CPU in 19.571 seconds
...
Count = 17548478.
То же самое для сетки 10x10, рассчитанной примерно за 6 минут (~ 2 миллиарда выводов):
?- placement(10, 10, Vs, Sat), sat_count(Sat, Count).
Count = 140547294509.
И в сетке 11x11, рассчитанной примерно за полчаса (~ 9 миллиардов выводов):
?- placement(11, 11, Vs, Sat), sat_count(Sat, Count).
Count = 15339263199580.
Наконец, и, возможно, наиболее важно, этот подход работает для любой формы плиток и не ограничивается квадратами или прямоугольниками. Например, для обработки квадратов 1x1 и формы треугольника, а также его вертикальных и горизонтальных отражений используйте следующее определение: tile_matrix/1:
tile_matrix([[1]]).
tile_matrix(T) :-
T0 = [[1,1,1,1],
[1,1,1,0],
[1,1,0,0],
[1,0,0,0]],
( T = T0
; maplist(reverse, T0, T)
; reverse(T0, T)
).
Позволяя использовать каждую из этих фигур от 0 до 7 раз на доске 9x7, я получаю, через минуту или около того, Count = 58665048314 решения.
Вот один из них, выбранный наугад:
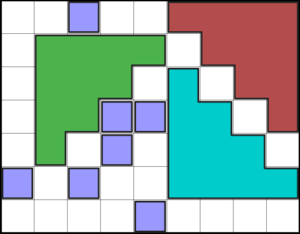
Подобрать решения таким образом, что каждое из них одинаково вероятно, также довольно просто с CLP(B), даже если число решений слишком велико, чтобы перечислить их явно.
Я закодировал в SWI-Пролог
/* File: pack_squares.lp
Author: Carlo,,,
Created: Nov 29 2012
Purpose: http://stackru.com/questions/13623775/prolog-constraint-processing-packing-squares
*/
:- module(pack_squares, [pack_squares/0]).
:- [library(clpfd)].
pack_squares :-
maplist(square, [5,4,3,2], Squares),
flatten(Squares, Coords),
not_overlap(Squares),
Coords ins 1..10,
label(Coords),
maplist(writeln, Squares),
draw_squares(Squares).
draw_squares(Squares) :-
forall(between(1, 10, Y),
( forall(between(1, 10, X),
sumpts(X, Y, Squares, 0)),
nl
)).
sumpts(_, _, [], S) :- write(S).
sumpts(X, Y, [[X1,Y1, X2,Y2]|Qs], A) :-
( ( X >= X1, X =< X2, Y >= Y1, Y =< Y2 )
-> B is A+X2-X1+1
; B is A
),
sumpts(X, Y, Qs, B).
square(D, [X1,Y1, X2,Y2]) :-
X1 + D - 1 #= X2,
Y1 + D - 1 #= Y2.
not_overlap([_]).
not_overlap([A,B|L]) :-
not_overlap(A, [B|L]),
!, not_overlap([B|L]).
not_overlap(_, []).
not_overlap(Q, [R|Rs]) :-
not_overlap_c(Q, R),
not_overlap_c(R, Q),
not_overlap(Q, Rs).
not_overlap_c([X1,Y1, X2,Y2], Q) :-
not_inside(X1,Y1, Q),
not_inside(X1,Y2, Q),
not_inside(X2,Y1, Q),
not_inside(X2,Y2, Q).
not_inside(X,Y, [X1,Y1, X2,Y2]) :-
X #< X1 #\/ X #> X2 #\/ Y #< Y1 #\/ Y #> Y2.
вот последние строки, отображаемые при запуске ?- aggregate_all(count,pack_squares,C)., в частности, C считает общее количество мест размещения
...
0002255555
0002255555
[6,6,10,10]
[7,2,10,5]
[4,3,6,5]
[5,1,6,2]
0000220000
0000224444
0003334444
0003334444
0003334444
0000055555
0000055555
0000055555
0000055555
0000055555
C = 169480.
Вот решение, в котором дизъюнкция занимает только одну строку:
% disjoint(+Rectangle, +Rectangle)
disjoint([XA1,XA2,YA1,YA2],[XB1,XB2,YB1,YB2]) :-
XB1 #>= XA2 #\/ XA1 #>= XB2 #\/
YB1 #>= YA2 #\/ YA1 #>= YB2.
Настройка модели и маркировка работают следующим образом:
% squares(-List)
squares(L) :-
maplist(square, [2,3,4,5], L),
term_variables(L, V),
place(L),
label(V).
% square(+Integer, -Rectangle)
square(S, [X1,X2,Y1,Y2]) :-
X1 in 0..8,
X2 in 1..9,
Y1 in 0..6,
Y2 in 1..7,
X2 #= X1+S,
Y2 #= Y1+S.
% place(+List)
place([]).
place([A|L]) :-
place(L, A),
place(L).
% place(+List, +Rectangle)
place([], _).
place([A|L], B) :-
disjoint(A, B),
place(L, B).
Вот пример запуска:
Jekejeke Prolog 3, Runtime Library 1.3.7 (May 23, 2019)
?- squares(L), show(L).
555554444
555554444
555554444
555554444
55555333.
22...333.
22...333.
L = [[0,2,5,7],[5,8,4,7],[5,9,0,4],[0,5,0,5]]