Как обнаружить сдвиг между изображениями

Question

Я анализирую несколько изображений и должен быть в состоянии определить, смещены ли они по сравнению с эталонным изображением. Цель состоит в том, чтобы определить, перемещалась ли камера вообще между съемками изображений. В идеале я хотел бы иметь возможность исправить смещение, чтобы все еще выполнять анализ, но как минимум мне нужно уметь определить, смещено ли изображение, и отбросить его, если оно превышает определенный порог.

Вот несколько примеров изменений в изображении, которые я хотел бы обнаружить:

Я буду использовать первое изображение в качестве эталона, а затем сравнивать все следующие изображения с ним, чтобы выяснить, смещены ли они. Изображения серого цвета (они просто отображаются в цвете с использованием тепловой карты) и хранятся в двумерном массиве. Есть идеи, как я могу это сделать? Я бы предпочел использовать уже установленные пакеты (scipy, numpy, PIL, matplotlib).

Answer 1

Как Lukas Graf подсказки, вы ищете взаимную корреляцию. Хорошо работает, если:

1. Масштаб ваших изображений существенно не меняется.
2. В изображениях нет изменений поворота.
3. На изображениях нет существенного изменения освещенности.

Для простых переводов взаимная корреляция очень хороша.

Самый простой инструмент взаимной корреляции scipy.signal.correlate, Однако он использует тривиальный метод для взаимной корреляции, который является O(n^4) для двумерного изображения с длиной стороны n. На практике с вашими изображениями это займет очень много времени.

Тем лучше scipy.signal.fftconvolve как свертка и корреляция тесно связаны между собой.

Что-то вроде этого:

import numpy as np
import scipy.signal

def cross_image(im1, im2):
   # get rid of the color channels by performing a grayscale transform
   # the type cast into 'float' is to avoid overflows
   im1_gray = np.sum(im1.astype('float'), axis=2)
   im2_gray = np.sum(im2.astype('float'), axis=2)

   # get rid of the averages, otherwise the results are not good
   im1_gray -= np.mean(im1_gray)
   im2_gray -= np.mean(im2_gray)

   # calculate the correlation image; note the flipping of onw of the images
   return scipy.signal.fftconvolve(im1_gray, im2_gray[::-1,::-1], mode='same')

Смешно выглядящая индексация im2_gray[::-1,::-1] поворачивает его на 180° (отражает как по горизонтали, так и по вертикали). В этом разница между сверткой и корреляцией, корреляция - это свертка со вторым отраженным сигналом.

Теперь, если мы просто сопоставим первое (самое верхнее) изображение с самим собой, мы получим:

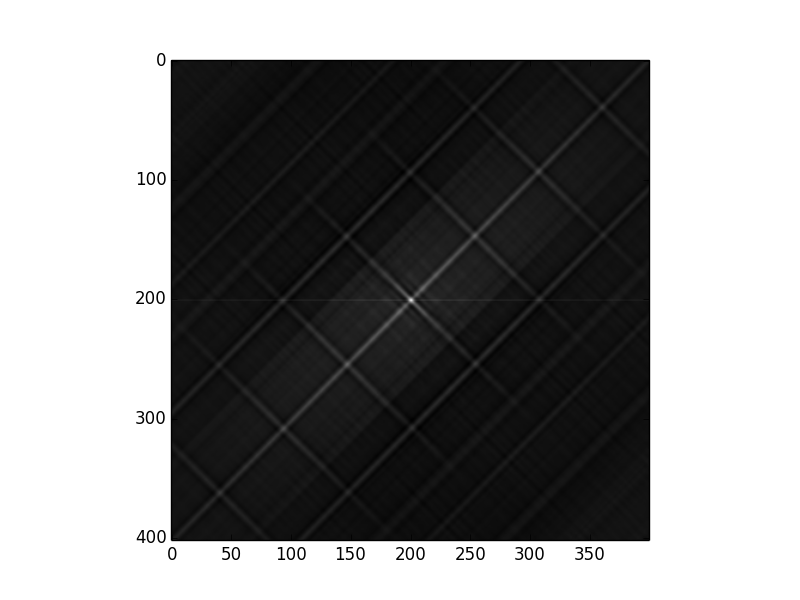
Это дает меру самоподобия изображения. Самая яркая точка находится в точке (201, 200), которая находится в центре изображения (402, 400).

Самые яркие координаты пятна можно найти:

np.unravel_index(np.argmax(corr_img), corr_img.shape)

Линейное положение самого яркого пикселя возвращается argmax, но он должен быть преобразован обратно в 2D координаты с unravel_index,

Далее мы попробуем то же самое, сопоставив первое изображение со вторым:

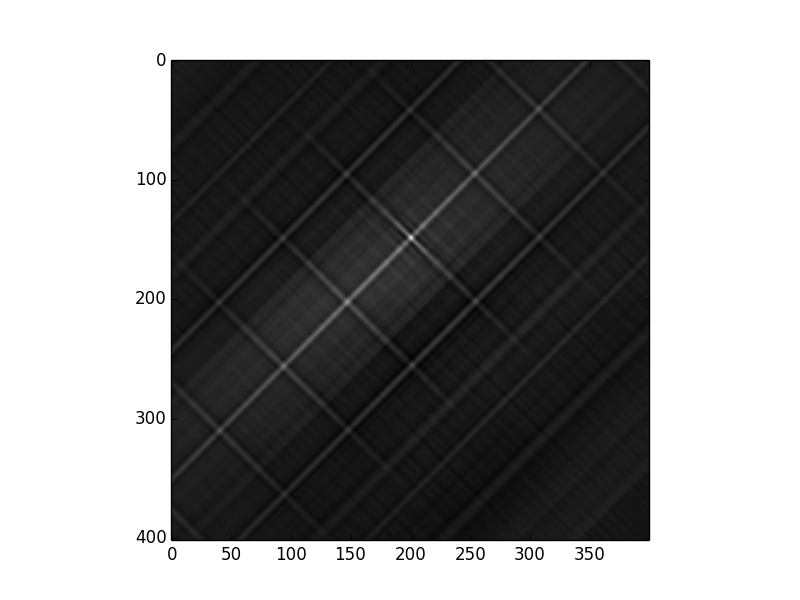
Изображение корреляции выглядит аналогично, но наилучшая корреляция переместилась на (149 200), то есть на 52 пикселя вверх по изображению. Это смещение между двумя изображениями.

---

Кажется, это работает с этими простыми изображениями. Однако также могут быть ложные корреляционные пики, и любая из проблем, изложенных в начале этого ответа, может испортить результаты.

В любом случае вы должны рассмотреть возможность использования оконной функции. Выбор функции не так важен, пока что-то используется. Кроме того, если у вас есть проблемы с небольшими изменениями поворота или масштаба, попробуйте сопоставить несколько небольших областей с окружающим изображением. Это даст вам разные смещения в разных положениях изображения.

Answer 2

Как сказал Бхарат, другой использует функции просеивания и Ransac:

import numpy as np
import cv2
from matplotlib import pyplot as plt

def crop_region(path, c_p):
    """
      This function crop the match region in the input image
      c_p: corner points
    """    
    # 3 or 4 channel as the original
    img = cv2.imread(path, -1)

    # mask 
    mask = np.zeros(img.shape, dtype=np.uint8) 

    # fill the the match region 
    channel_count = img.shape[2]  
    ignore_mask_color = (255,)*channel_count
    cv2.fillPoly(mask, c_p, ignore_mask_color)

    # apply the mask
    matched_region = cv2.bitwise_and(img, mask)

    return matched_region

def features_matching(path_temp,path_train):
    """
          Function for Feature Matching + Perspective Transformation
    """       
    img1 = cv2.imread(path_temp, 0)   # template
    img2 = cv2.imread(path_train, 0)   # input image

    min_match=10

    # SIFT detector
    sift = cv2.xfeatures2d.SIFT_create()

    # extract the keypoints and descriptors with SIFT

    kps1, des1 = sift.detectAndCompute(img1,None)
    kps2, des2 = sift.detectAndCompute(img2,None)

    FLANN_INDEX_KDTREE = 0
    index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
    search_params = dict(checks = 50)

    flann = cv2.FlannBasedMatcher(index_params, search_params)

    matches = flann.knnMatch(des1, des2, k=2)

    # store all the good matches (g_matches) as per Lowe's ratio 
    g_match = []
    for m,n in matches:
        if m.distance < 0.7 * n.distance:
            g_match.append(m)
    if len(g_match)>min_match:
        src_pts = np.float32([ kps1[m.queryIdx].pt for m in g_match ]).reshape(-1,1,2)
        dst_pts = np.float32([ kps2[m.trainIdx].pt for m in g_match ]).reshape(-1,1,2)

        M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC,5.0)
        matchesMask = mask.ravel().tolist()

        h,w = img1.shape
        pts = np.float32([ [0,0],[0,h-1],[w-1,h-1],[w-1,0] ]).reshape(-1,1,2)
        dst = cv2.perspectiveTransform(pts,M)

        img2 = cv2.polylines(img2, [np.int32(dst)], True, (0,255,255) , 3, cv2.LINE_AA)

    else:
        print "Not enough matches have been found! - %d/%d" % (len(g_match), min_match)
        matchesMask = None

    draw_params = dict(matchColor = (0,255,255), 
                       singlePointColor = (0,255,0),
                       matchesMask = matchesMask, # only inliers
                       flags = 2)
    # region corners    
    cpoints=np.int32(dst)
    a, b,c = cpoints.shape

    # reshape to standard format
    c_p=cpoints.reshape((b,a,c))  

    # crop matching region
    matching_region = crop_region(path_train, c_p)

    img3 = cv2.drawMatches(img1, kps1, img2, kps2, g_match, None, **draw_params)
    return (img3,matching_region)

Answer 3

Еще один способ решить эту проблему - вычислить точки просеивания на обоих изображениях, использовать RANSAC, чтобы избавиться от выбросов, а затем найти решение для перевода с использованием метода наименьших квадратов.