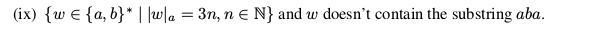Разработка DFA (алфавит "a" и "b"): число "a" в строке должно быть кратно 3, и строка не должна содержать "aba"

Question

Вот проблема:

И вот моя линия рассуждений, когда я впервые наткнулся на это:

• Этот кажется трудным
• Найти регулярное выражение для него кажется сложным, поэтому я не могу пойти по этому пути, чтобы преобразовать регулярное выражение в DFA
• Поэтому я решил решить первую часть проблемы: принять строку, чье число "а" кратно 3. Это довольно просто, вам просто нужно 3 состояния: 1,2,3 с 1 в качестве начального состояния, если есть вход "a", вы переходите к следующему, если это "b", вы остаетесь в этом состоянии, и начальное состояние также является конечным. Но здесь, в этом упражнении, эти 3 государства на самом деле будут 3 "большими" государствами. Тогда проблемой становится проектирование внутренних органов этих больших состояний и того, как они взаимодействуют.

У меня не было выбора, кроме как использовать догадки, чтобы прийти к решению. Вот что я придумал (1,2,3 - это завершающие состояния, 3 - начальное состояние, а также 7 и 9 оба переходят в 1, если получен вход "а"): 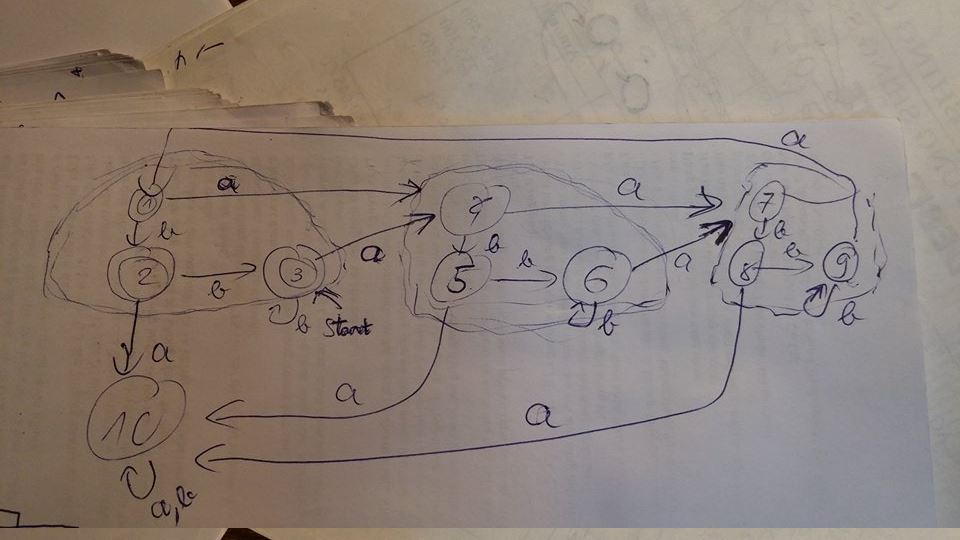Я также использовал минимизацию DFA на этом и обнаружил, что это уже минимально. Однако учебники дают другое решение: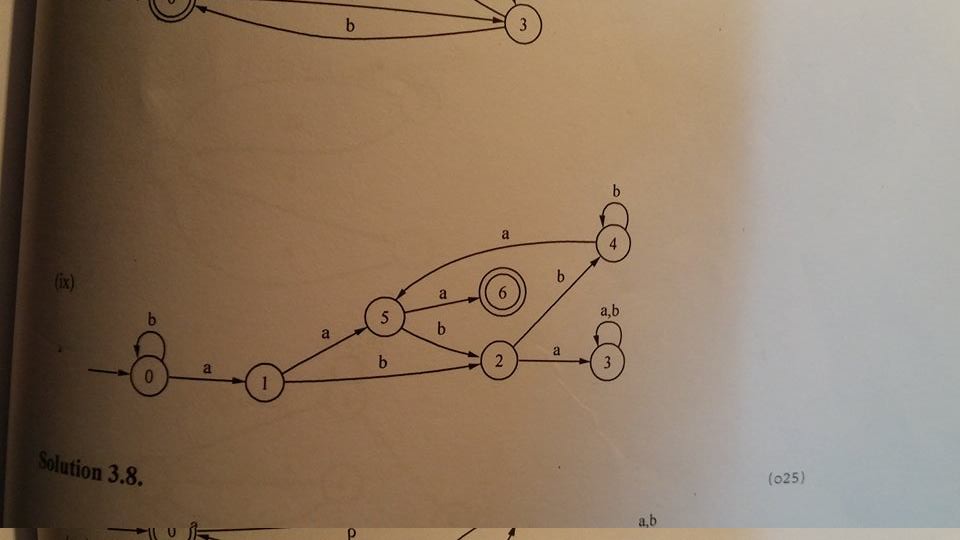

Но я не понимаю, как это правильно! Я просто не могу понять:(. И я даже не знаю, правильно ли мое решение на 100%. Пожалуйста, помогите мне, большое спасибо:)

Answer 1

Ваш ответ кажется правильным. Я не тщательно это доказал, но логика довольно ясна. Кроме того, я написал программу на Python для ее проверки:

def accepts(transitions,initial,accepting,s):
    state = initial
    for c in s:
        state = transitions[state][c]
    return state in accepting

dfa = {1:{'a':4, 'b':2},
       2:{'a':10, 'b':3},
       3:{'a':4, 'b':3},
       4:{'a':7, 'b':5},
       5:{'a':10, 'b':6},
       6:{'a':7, 'b':6},
       7:{'a':1, 'b':8},
       8:{'a':10, 'b':9},
       9:{'a':1, 'b':9},
       10:{'a':10, 'b':10}}

def dfaTest(s):
    return accepts(dfa,3,{1,2,3},s)

def valid(s):
    return s.count('a') % 3 == 0 and not 'aba' in s

import random

tests = [''.join(random.choice(['a','b']) for j in range(100)) for i in range(1,1001)]

print(all(valid(s) == dfaTest(s) for s in tests))

Работа функции accepts объясняется в этом ответе. Я настроил его в соответствии с вашей диаграммой. Для стресс-теста я сгенерировал 100000 случайных входных данных, длина которых варьируется от 1 до 1000, а затем сравнил выходные данные DFA с прямой проверкой состояния. Каждый раз, когда я запускаю этот код, вывод является удовлетворительным True,

Чтобы проверить отдельные строки:

>>> dfaTest('ababba')
False
>>> dfaTest('abbabba')
True