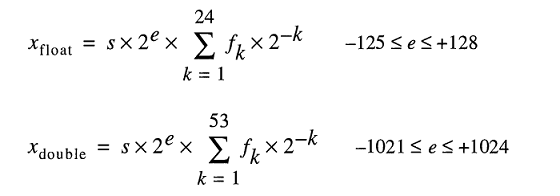Математика с плавающей точкой нарушена?

Question

Математика с плавающей точкой нарушена?

Рассмотрим следующий код:

0.1 + 0.2 == 0.3  ->  false

0.1 + 0.2         ->  0.30000000000000004

Почему эти неточности случаются?

3938

math floating-point language-agnostic floating-accuracy

Источник

user62118 25 фев '09 в 21:39

39 ответов

Решение

Перспектива разработчика оборудования

Я считаю, что я должен добавить точку зрения разработчика оборудования, так как я проектирую и собираю оборудование с плавающей запятой. Знание причины ошибки может помочь в понимании того, что происходит в программном обеспечении, и, в конечном счете, я надеюсь, что это поможет объяснить причины возникновения ошибок с плавающей запятой и их накопление с течением времени.

1. Обзор

С инженерной точки зрения, большинство операций с плавающей запятой будут иметь некоторый элемент ошибки, поскольку требуется, чтобы аппаратное обеспечение, которое выполняет вычисления с плавающей запятой, имело ошибку не более половины одного модуля в последнем месте. Следовательно, большое количество аппаратного обеспечения будет останавливаться с точностью, необходимой только для того, чтобы выдать ошибку менее половины одного блока в последнем месте для одной операции, что особенно проблематично при делении с плавающей запятой. То, что составляет одну операцию, зависит от того, сколько операндов принимает блок. Для большинства это два, но некоторые единицы принимают 3 или более операндов. Из-за этого нет гарантии, что повторные операции приведут к желаемой ошибке, так как ошибки накапливаются со временем.

2. Стандарты

Большинство процессоров соответствуют стандарту IEEE-754, но некоторые используют денормализованные или другие стандарты. Например, в IEEE-754 есть денормализованный режим, который позволяет представлять очень маленькие числа с плавающей запятой за счет точности. Следующее, однако, будет охватывать нормализованный режим IEEE-754, который является типичным режимом работы.

В стандарте IEEE-754 разработчикам аппаратного обеспечения разрешается любое значение error/epsilon, если в последнем месте оно составляет менее половины одного модуля, а результат должен составлять менее половины одного модуля в последнем место для одной операции. Это объясняет, почему при повторных операциях ошибки складываются. Для двойной точности IEEE-754 это 54-й бит, поскольку 53 бита используются для представления числовой части (нормализованной), также называемой мантиссой, числа с плавающей запятой (например, 5.3 в 5.3e5). В следующих разделах более подробно рассматриваются причины аппаратной ошибки при различных операциях с плавающей запятой.

3. Причина ошибки округления в делении

Основной причиной ошибки в делении с плавающей запятой являются алгоритмы деления, используемые для вычисления отношения. Большинство компьютерных систем вычисляют деление, используя умножение на обратное, главным образом в Z=X/Y, Z = X * (1/Y), Деление вычисляется итеративно, то есть каждый цикл вычисляет некоторые биты частного до тех пор, пока не будет достигнута желаемая точность, которая для IEEE-754 равна нулю с ошибкой менее одной единицы в последнем месте. Таблица обратных значений Y (1/Y) называется таблицей выбора коэффициентов (QST) при медленном делении, а размер в битах таблицы коэффициентов выбора обычно равен ширине радиуса или числу битов. коэффициент, вычисленный в каждой итерации, плюс несколько защитных битов. Для стандарта IEEE-754 с двойной точностью (64-битная) это будет размер радиуса делителя плюс несколько защитных битов k, где k>=2, Так, например, типичная таблица выбора частного для делителя, который вычисляет 2 бита частного за раз (основание 4), будет 2+2= 4 биты (плюс несколько необязательных битов).

3.1 Ошибка округления деления: аппроксимация взаимности

То, какие обратные величины находятся в таблице коэффициентов выбора, зависит от метода деления: медленное деление, такое как деление СТО, или быстрое деление, такое как деление Гольдшмидта; каждая запись модифицируется в соответствии с алгоритмом деления в попытке получить минимально возможную ошибку. В любом случае, тем не менее, все обратные величины являются приблизительными значениями действительной обратной величины и вносят некоторый элемент ошибки. Оба метода - с медленным делением и с быстрым делением - вычисляют частное итеративно, т. Е. Некоторое число битов частного вычисляется на каждом шаге, затем результат вычитается из делимого, и делитель повторяет шаги, пока ошибка не станет меньше половины одного Блок на последнем месте. Методы медленного деления вычисляют фиксированное количество цифр отношения на каждом шаге и, как правило, дешевле в построении, а методы быстрого деления вычисляют переменное количество цифр на шаг и, как правило, стоят дороже. Самая важная часть методов деления состоит в том, что большинство из них полагаются на повторное умножение на приближение обратного, поэтому они подвержены ошибкам.

4. Ошибки округления в других операциях: усечение

Еще одной причиной ошибок округления во всех операциях являются различные режимы усечения окончательного ответа, которые допускает IEEE-754. Есть усечение, округление к нулю, округление до ближайшего (по умолчанию), округление вниз и округление вверх. Все методы вводят элемент ошибки менее чем на одну единицу в последнем месте для одной операции. Со временем и повторяющимися операциями усечение также добавляет к результирующей ошибке. Эта ошибка усечения особенно проблематична при возведении в степень, которая включает в себя некоторую форму повторного умножения.

5. Повторные операции

Поскольку аппаратное обеспечение, которое выполняет вычисления с плавающей запятой, должно давать только результат с ошибкой менее половины одного блока в последнем месте для одной операции, ошибка будет расти по сравнению с повторяющимися операциями, если их не наблюдать. Это причина того, что в вычислениях, которые требуют ограниченной ошибки, математики используют такие методы, как использование четного округленного до ближайшего числа в последнем месте IEEE-754, потому что с течением времени ошибки с большей вероятностью отменяют друг друга out, и Interval Arithmetic в сочетании с вариациями режимов округления IEEE 754 для прогнозирования ошибок округления и их исправления. Из-за его низкой относительной ошибки по сравнению с другими режимами округления, округление до ближайшей четной цифры (на последнем месте) является режимом округления по умолчанию IEEE-754.

Обратите внимание, что режим округления по умолчанию ( четная цифра округления до ближайшего на последнем месте) гарантирует ошибку менее одной половины одного блока на последнем месте для одной операции. Использование только усечения, округления и округления может привести к ошибке, которая больше, чем половина одного блока в последнем месте, но меньше, чем один блок в последнем месте, поэтому эти режимы не рекомендуются, если они не используется в интервальной арифметике.

6. Резюме

Короче говоря, фундаментальная причина ошибок в операциях с плавающей запятой заключается в комбинации усечения в аппаратном обеспечении и усечения обратной в случае деления. Так как стандарт IEEE-754 требует только ошибки менее половины одного блока в последнем месте для одной операции, ошибки с плавающей запятой при повторных операциях будут складываться, если не будут исправлены.

726

Источник

user2244559 18 апр '13 в 11:52

Когда вы конвертируете.1 или 1/10 в основание 2 (двоичное), вы получаете повторяющийся шаблон после десятичной точки, точно так же, как пытаетесь представить 1/3 в основании 10. Значение не является точным, и поэтому вы не можете сделать точная математика с ним, используя обычные методы с плавающей запятой.

645

Источник

user3043 25 фев '09 в 21:43

Большинство ответов здесь обращаются к этому вопросу в очень сухих, технических терминах. Я хотел бы рассмотреть это в терминах, которые могут понять нормальные люди.

Представьте, что вы пытаетесь нарезать пиццу. У вас есть роботизированный нож для пиццы, который может разрезать кусочки пиццы ровно пополам. Это может вдвое уменьшить целую пиццу, или это может вдвое сократить существующий кусок, но в любом случае, вдвое всегда точно.

Этот резак для пиццы имеет очень тонкие движения, и если вы начнете с целой пиццы, а затем разделите ее пополам и продолжите каждый раз делить на две части наименьший ломтик, вы можете сделать его вдвое 53 раза, прежде чем ломтик станет слишком маленьким даже для его высокоточных способностей, В этот момент вы больше не можете вдвое разделить этот очень тонкий срез, но должны либо включить, либо исключить его как есть.

Теперь, как бы вы нарезали все ломтики таким образом, чтобы можно было получить одну десятую (0,1) или одну пятую (0,2) пиццы? На самом деле подумайте об этом, и попробуйте решить это. Вы даже можете попробовать настоящую пиццу, если у вас под рукой мифическая прецизионная пиццерия.:-)

Конечно, большинство опытных программистов знают реальный ответ, который заключается в том, что невозможно собрать точную десятую или пятую части пиццы, используя эти кусочки, независимо от того, насколько хорошо вы их нарезаете. Вы можете сделать довольно хорошее приближение, и если вы сложите приближение 0,1 с приближением 0,2, вы получите довольно хорошее приближение 0,3, но это все еще только приближение.

Для чисел с двойной точностью (то есть точности, которая позволяет вам вдвое сократить пиццу в 53 раза), числа, которые немедленно меньше и больше 0,1, составляют 0,09999999999999999167332731531132594682276248931884765625 и 0,1000000000000000055511151231257827021181583404541015625. Последнее немного ближе к 0,1, чем первое, поэтому числовой синтаксический анализатор при вводе 0,1 будет благоприятствовать последнему.

(Разница между этими двумя числами заключается в "наименьшем срезе", который мы должны решить либо включить, который вводит смещение вверх, либо исключить, который вводит смещение вниз. Техническим термином для этого наименьшего среза является ulp.)

В случае 0,2 числа все одинаковы, только увеличены в 2 раза. Опять же, мы предпочитаем значение, немного превышающее 0,2.

Обратите внимание, что в обоих случаях аппроксимации для 0,1 и 0,2 имеют небольшое смещение вверх. Если мы добавим достаточное количество этих смещений, они будут отталкивать число все дальше и дальше от того, что мы хотим, и на самом деле, в случае 0,1 + 0,2, смещение достаточно велико, чтобы полученное число больше не было ближайшим числом до 0,3.

В частности, 0,1 + 0,2 действительно 0.1000000000000000055511151231257827021181583404541015625 + 0.200000000000000011102230246251565404236316680908203125 = 0.3000000000000000444089209850062616169452667236328125, тогда как число ближе к 0,3 фактически 0,299999999999999988897769753748434595763683319091796875.

PS Некоторые языки программирования также предоставляют нарезчики пиццы, которые могут разбивать ломтики на ровные десятые доли. Хотя такие ножницы для пиццы являются редкостью, если у вас есть доступ к одному, вы должны использовать его, когда важно иметь возможность получить ровно одну десятую или одну пятую части.

(Первоначально опубликовано на Quora.)

391

Источник

user13 20 ноя '14 в 02:39

Ошибки округления с плавающей точкой. 0,1 не может быть представлен с такой же точностью в базе-2, как в базе-10, из-за отсутствующего простого множителя, равного 5. Точно так же, как 1/3 занимает бесконечное число цифр для представления в десятичной форме, но равен "0,1" в базе-3, 0.1 принимает бесконечное количество цифр в base-2, а не в base-10. И у компьютеров нет бесконечного количества памяти.

233

Источник

user18515 25 фев '09 в 21:41

Мой ответ довольно длинный, поэтому я разделил его на три части. Поскольку вопрос касается математики с плавающей запятой, я акцентировал внимание на том, что на самом деле делает машина. Я также определил двойную (64-битную) точность, но аргумент одинаково применим к любой арифметике с плавающей запятой.

преамбула

Число двоичного формата с плавающей запятой IEEE 754 с двоичной точностью (двоичное число 64) представляет число в форме

значение = (-1)^ с * (1.м ₅₁ м ₅₀... м ₂ м ₁ м ₀) ₂ * 2 ^e-1023

в 64 битах:

Первый бит это знаковый бит: 1 если число отрицательное, 0 в противном случае ¹.
Следующие 11 битов являются показателем степени, который смещен на 1023. Другими словами, после считывания показательных битов из числа с двойной точностью, 1023 необходимо вычесть, чтобы получить степень двух.
Остальные 52 бита являются значимыми (или мантиссами). В мантиссе подразумевается 1. всегда опускается на ^2, поскольку старший бит любого двоичного значения 1,

¹ - IEEE 754 допускает концепцию подписанного нуля - +0 а также -0 трактуются по-разному: 1 / (+0) положительная бесконечность; 1 / (-0) отрицательная бесконечность. Для нулевых значений биты мантиссы и экспоненты равны нулю. Примечание: нулевые значения (+0 и -0) явно не классифицируются как денормальные ².

² - Это не относится к ненормальным числам, у которых показатель смещения равен нулю (и подразумевается 0.). Диапазон числовых чисел двойной точности равен d _min ≤ | x | ≤ d _max, где d _min (наименьшее представимое ненулевое число) составляет 2 ^{-1023 - 51} (≈ 4.94 * 10 ^-324) и d _max (наибольшее денормальное число, для которого мантисса целиком состоит из 1 s) составляет 2 ^{-1023 + 1} - 2 ^{-1023 - 51} (≈ 2,225 * 10 ^-308).

Превращение числа с двойной точностью в двоичное

Существует много онлайн-конвертеров для преобразования числа с плавающей запятой двойной точности в двоичное (например, на сайте binaryconvert.com), но здесь приведен пример кода C# для получения представления IEEE 754 для числа двойной точности (я разделяю три части двоеточиями (:):

public static string BinaryRepresentation(double value)
{
    long valueInLongType = BitConverter.DoubleToInt64Bits(value);
    string bits = Convert.ToString(valueInLongType, 2);
    string leadingZeros = new string('0', 64 - bits.Length);
    string binaryRepresentation = leadingZeros + bits;

    string sign = binaryRepresentation[0].ToString();
    string exponent = binaryRepresentation.Substring(1, 11);
    string mantissa = binaryRepresentation.Substring(12);

    return string.Format("{0}:{1}:{2}", sign, exponent, mantissa);
}

Приступая к делу: оригинальный вопрос

(Перейти к нижней части для версии TL;DR)

Cato Johnston (задающий вопрос) спросил, почему 0,1 + 0,2!= 0,3.

Написанные в двоичном виде (с двоеточиями, разделяющими три части), представления значений IEEE 754:

0.1 => 0:01111111011:1001100110011001100110011001100110011001100110011010
0.2 => 0:01111111100:1001100110011001100110011001100110011001100110011010

Обратите внимание, что мантисса состоит из повторяющихся цифр 0011, Это является ключом к тому, почему есть какая-либо ошибка в вычислениях - 0,1, 0,2 и 0,3 не могут быть представлены в двоичном виде точно в конечном количестве двоичных разрядов, больше чем 1/9, 1/3 или 1/7 могут быть представлены точно в десятичные цифры.

Преобразование показателей степени в десятичное, удаление смещения и повторное добавление подразумеваемых 1 (в квадратных скобках) 0,1 и 0,2:

0.1 = 2^-4 * [1].1001100110011001100110011001100110011001100110011010
0.2 = 2^-3 * [1].1001100110011001100110011001100110011001100110011010

Чтобы добавить два числа, показатель должен быть одинаковым, то есть:

0.1 = 2^-3 *  0.1100110011001100110011001100110011001100110011001101(0)
0.2 = 2^-3 *  1.1001100110011001100110011001100110011001100110011010
sum = 2^-3 * 10.0110011001100110011001100110011001100110011001100111

Поскольку сумма не имеет вид 2 ⁿ * 1. {bbb}, мы увеличиваем показатель степени на единицу и сдвигаем десятичную (двоичную) точку, чтобы получить:

sum = 2^-2 * 1.0011001100110011001100110011001100110011001100110011(1)

Теперь в мантиссе 53 бита (53-я в квадратных скобках в строке выше). Режим округления по умолчанию для IEEE 754 - " Округление до ближайшего " - т. Е. Если число x попадает между двумя значениями a и b, выбирается значение, где младший значащий бит равен нулю.

a = 2^-2 * 1.0011001100110011001100110011001100110011001100110011
x = 2^-2 * 1.0011001100110011001100110011001100110011001100110011(1)
b = 2^-2 * 1.0011001100110011001100110011001100110011001100110100

Обратите внимание, что a и b отличаются только последним битом; ...0011 + 1 знак равно ...0100, В этом случае значение с наименьшим значащим нулевым битом равно b, поэтому сумма равна:

sum = 2^-2 * 1.0011001100110011001100110011001100110011001100110100

TL;DR

Пишу 0.1 + 0.2 в двоичном представлении IEEE 754 (с двоеточиями, разделяющими три части) и сравнивая его с 0.3, это (я поставил отдельные биты в квадратных скобках):

0.1 + 0.2 => 0:01111111101:0011001100110011001100110011001100110011001100110[100]
0.3       => 0:01111111101:0011001100110011001100110011001100110011001100110[011]

Преобразованные обратно в десятичные, эти значения:

0.1 + 0.2 => 0.300000000000000044408920985006...
0.3       => 0.299999999999999988897769753748...

Разница составляет ровно 2 ^-54, что составляет ~ 5.5511151231258 × 10 ^-17 - незначительно (для многих приложений) по сравнению с исходными значениями.

Сравнение последних нескольких битов числа с плавающей запятой по своей природе опасно, и каждый, кто прочитает знаменитую статью " Что должен знать каждый компьютерный специалист об арифметике с плавающей запятой " (которая охватывает все основные части этого ответа).

Большинство калькуляторов используют дополнительные защитные цифры, чтобы обойти эту проблему, как это 0.1 + 0.2 даст 0.3: последние несколько бит округлены.

155

Источник

user1364007 23 фев '15 в 17:15

В дополнение к другим правильным ответам вы можете рассмотреть возможность масштабирования ваших значений, чтобы избежать проблем с арифметикой с плавающей точкой.

Например:

var result = 1.0 + 2.0;     // result === 3.0 returns true

... вместо:

var result = 0.1 + 0.2;     // result === 0.3 returns false

Выражение 0.1 + 0.2 === 0.3 возвращается false в JavaScript, но, к счастью, целочисленная арифметика с плавающей запятой является точной, поэтому ошибок масштабирования можно избежать с помощью масштабирования.

В качестве практического примера, чтобы избежать проблем с плавающей запятой, где точность имеет первостепенное значение, рекомендуется¹ обрабатывать деньги как целое число, представляющее количество центов: 2550 центы вместо 25.50 долларов.

¹ Дуглас Крокфорд: JavaScript: Хорошие части: Приложение A - Ужасные части (стр. 105).

142

Источник

user222908 09 апр '10 в 12:25

Числа с плавающей точкой, хранящиеся в компьютере, состоят из двух частей: целого числа и показателя степени, к которому берется основание и умножается на целочисленную часть.

Если компьютер работал в базе 10, 0.1 было бы 1 x 10⁻¹, 0.2 было бы 2 x 10⁻¹, а также 0.3 было бы 3 x 10⁻¹, Целочисленная математика проста и точна, поэтому добавление 0.1 + 0.2 очевидно, приведет к 0.3,

Компьютеры обычно не работают в базе 10, они работают в базе 2. Вы можете получить точные результаты для некоторых значений, например 0.5 является 1 x 2⁻¹ а также 0.25 является 1 x 2⁻²и добавление их приводит к 3 x 2⁻², или же 0.75, Именно так.

Проблема возникает с числами, которые могут быть представлены точно в базе 10, но не в базе 2. Эти числа должны быть округлены до их ближайшего эквивалента. Предполагая, что очень распространенный IEEE 64-битный формат с плавающей запятой, ближайший номер к 0.1 является 3602879701896397 x 2⁻⁵⁵и ближайший номер к 0.2 является 7205759403792794 x 2⁻⁵⁵; сложение их вместе приводит к 10808639105689191 x 2⁻⁵⁵или точное десятичное значение 0.3000000000000000444089209850062616169452667236328125, Числа с плавающей точкой обычно округляются для отображения.

68

Источник

user5987 16 мар '16 в 05:27

Чтобы предложить лучшее решение, я могу сказать, что обнаружил следующий метод:

parseFloat((0.1 + 0.2).toFixed(10)) => Will return 0.3

Позвольте мне объяснить, почему это лучшее решение. Как уже упоминалось в ответах выше, для решения проблемы рекомендуется использовать готовую функцию toFixed() Javascript. Но, скорее всего, вы столкнетесь с некоторыми проблемами.

Представьте, что вы собираетесь сложить два числа с плавающей точкой, как 0.2 а также 0.7 вот: 0.2 + 0.7 = 0.8999999999999999,

Ваш ожидаемый результат был 0.9 это означает, что в этом случае вам нужен результат с точностью до 1 цифры. Так что вы должны были использовать (0.2 + 0.7).tofixed(1) но вы не можете просто дать определенный параметр toFixed(), так как он зависит от заданного числа, например

`0.22 + 0.7 = 0.9199999999999999`

В этом примере вам нужна точность в 2 цифры, поэтому она должна быть toFixed(2) Итак, какой должен быть параметр, чтобы соответствовать каждому заданному числу с плавающей точкой?

Вы можете сказать, пусть это будет 10 в каждой ситуации:

(0.2 + 0.7).toFixed(10) => Result will be "0.9000000000"

Черт! Что вы собираетесь делать с этими нежелательными нулями после 9? Пришло время преобразовать это в float, чтобы сделать это, как вы хотите:

parseFloat((0.2 + 0.7).toFixed(10)) => Result will be 0.9

Теперь, когда вы нашли решение, лучше предложить его в виде такой функции:

function floatify(number){
           return parseFloat((number).toFixed(10));
        }

Давайте попробуем сами:

function floatify(number){
       return parseFloat((number).toFixed(10));
    }
 
function addUp(){
  var number1 = +$("#number1").val();
  var number2 = +$("#number2").val();
  var unexpectedResult = number1 + number2;
  var expectedResult = floatify(number1 + number2);
  $("#unexpectedResult").text(unexpectedResult);
  $("#expectedResult").text(expectedResult);
}
addUp();

input{
  width: 50px;
}
#expectedResult{
color: green;
}
#unexpectedResult{
color: red;
}

<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script>
<input id="number1" value="0.2" onclick="addUp()" onkeyup="addUp()"/> +
<input id="number2" value="0.7" onclick="addUp()" onkeyup="addUp()"/> =
<p>Expected Result: <span id="expectedResult"></span></p>
<p>Unexpected Result: <span id="unexpectedResult"></span></p>

Вы можете использовать это так:

var x = 0.2 + 0.7;
floatify(x);  => Result: 0.9

Поскольку W3SCHOOLS предполагает, что есть и другое решение, вы можете умножить и разделить, чтобы решить проблему выше:

var x = (0.2 * 10 + 0.1 * 10) / 10;       // x will be 0.3

Имейте в виду, что (0.2 + 0.1) * 10 / 10 не будет работать вообще, хотя кажется, что то же самое! Я предпочитаю первое решение, так как я могу применить его как функцию, которая преобразует входной float в точный выходной float.

62

Источник

user4344976 07 авг '18 в 09:34

Ошибка округления с плавающей точкой. Из того, что должен знать каждый компьютерщик об арифметике с плавающей точкой:

Сжатие бесконечного числа действительных чисел в конечное число бит требует приблизительного представления. Хотя целых чисел бесконечно много, в большинстве программ результат целочисленных вычислений может храниться в 32 битах. Напротив, при любом фиксированном количестве битов большинство вычислений с действительными числами будут давать величины, которые не могут быть точно представлены с использованием такого количества битов. Поэтому результат вычисления с плавающей точкой часто должен быть округлен, чтобы соответствовать его конечному представлению. Эта ошибка округления является характерной особенностью вычисления с плавающей точкой.

53

Источник

user48495 25 фев '09 в 21:42

Мой обходной путь:

function add(a, b, precision) {
    var x = Math.pow(10, precision || 2);
    return (Math.round(a * x) + Math.round(b * x)) / x;
}

Точность относится к числу цифр, которые вы хотите сохранить после десятичной точки во время сложения.

39

Источник

user707258 26 дек '11 в 06:51

Нет, не разбито, но большинство десятичных дробей должно быть аппроксимировано

Резюме

Арифметика с плавающей запятой точна, к сожалению, она не очень хорошо согласуется с нашим обычным представлением чисел с основанием 10, поэтому оказывается, что мы часто даем в нее ввод, который немного отличается от того, что мы написали.

Даже простые числа, такие как 0,01, 0,02, 0,03, 0,04 ... 0,24, не могут быть представлены в виде двоичных дробей. Если вы подсчитаете 0,01, 0,02, 0,03 ..., то только до 0,25 вы получите первую дробь, представимую в базе ₂. Если вы попробуете это с использованием FP, ваш 0.01 был бы немного не таким, поэтому единственный способ добавить 25 из них до точного 0.25 потребовал бы длинной цепочки причинно-следственных связей, включающей защитные биты и округление. Трудно предсказать, поэтому мы вскидываем руки и говорим: "FP - это неточно", но это не совсем так.

Мы постоянно даем оборудованию FP что-то, что кажется простым в базе 10, но является повторяющейся частью в базе 2.

Как это случилось?

Когда мы пишем в десятичном виде, каждая дробь (в частности, каждый завершающий десятичный) является рациональным числом вида

а / (2 ^н х 5 ^м)

В двоичном коде мы получаем только 2 ⁿ член, то есть:

а / 2 ^н

Таким образом, в десятичном виде мы не можем представить _1/3. Поскольку основание 10 включает в себя 2 в качестве простого множителя, каждое число, которое мы можем записать в виде двоичной дроби, также может быть записано в виде дробной базы 10. Однако вряд ли все, что мы пишем как дробь с основанием _10, представимо в двоичном виде. В диапазоне от 0,01, 0,02, 0,03 до 0,99 в нашем формате FP могут быть представлены только три числа: 0,25, 0,50 и 0,75, поскольку они равны 1/4, 1/2 и 3/4, все числа с простым множителем, использующим только 2 ⁿ член.

В базе ₁₀ мы не можем представить _1/3. Но в двоичном коде мы не можем сделать _1/10 или _1/3.

Таким образом, хотя каждая двоичная дробь может быть записана в десятичном виде, обратное неверно. И на самом деле большинство десятичных дробей повторяются в двоичном формате.

Имея дело с этим

Разработчикам, как правило, дают указание сделать < сравнение epsilon, лучше посоветовать округлить до целочисленных значений (в библиотеке C: round() и roundf(), т. Е. Остаться в формате FP), а затем сравнить. Округление до определенной длины десятичной дроби решает большинство проблем с выводом.

Кроме того, о реальных проблемах с сокращением числа (проблемы, которые были изобретены FP на ранних, ужасно дорогих компьютерах), физические константы вселенной и все другие измерения известны только относительно небольшому числу значащих цифр, поэтому все проблемное пространство был "неточным" в любом случае. Точность FP не является проблемой в такого рода приложениях.

Вся проблема действительно возникает, когда люди пытаются использовать FP для подсчета бобов. Это работает для этого, но только если вы придерживаетесь целочисленных значений, что побеждает смысл его использования. Вот почему у нас есть все эти библиотеки программного обеспечения с десятичной дробью.

Мне нравится ответ Chris Jester-Young на "Пиццу", потому что он описывает реальную проблему, а не просто обычные пометки о "неточности". Если бы FP были просто "неточными", мы могли бы это исправить и сделали бы это десятилетия назад. Причина, по которой мы этого не делаем, заключается в том, что формат FP компактен и быстр, и это лучший способ сократить множество чисел. Кроме того, это наследие космической эры и гонки вооружений и ранних попыток решить большие проблемы с очень медленными компьютерами с использованием небольших систем памяти. (Иногда отдельные магнитные сердечники для 1-битного хранилища, но это уже другая история.)

Заключение

Если вы просто подсчитываете бины в банке, программные решения, которые в первую очередь используют десятичные строковые представления, работают превосходно. Но вы не можете делать квантовую хромодинамику или аэродинамику таким образом.

37

Источник

user140740 02 фев '16 в 23:49

Было опубликовано много хороших ответов, но я хотел бы добавить еще один.

Не все числа могут быть представлены числами с плавающей запятой / двойными числами. Например, число "0.2" будет представлено как "0.200000003" с одинарной точностью в стандарте IEEE754 с плавающей запятой.

Модель для хранения реальных чисел под капотом представляет числа с плавающей точкой в виде

Даже если вы можете напечатать 0.2 без труда, FLT_RADIX а также DBL_RADIX 2; не 10 для компьютера с FPU, который использует "Стандарт IEEE для двоичной арифметики с плавающей точкой (ISO/IEEE Std 754-1985)".

Поэтому немного сложно точно представить такие числа. Даже если вы укажете эту переменную явно без каких-либо промежуточных вычислений.

33

Источник

user1154447 05 окт '14 в 18:39

Немного статистики, связанной с этим известным вопросом двойной точности.

При сложении всех значений (a + b) с шагом 0,1 (от 0,1 до 100) вероятность ошибки точности составляет ~15%. Обратите внимание, что ошибка может привести к чуть большим или меньшим значениям. Вот некоторые примеры:

0.1 + 0.2 = 0.30000000000000004 (BIGGER)
0.1 + 0.7 = 0.7999999999999999 (SMALLER)
...
1.7 + 1.9 = 3.5999999999999996 (SMALLER)
1.7 + 2.2 = 3.9000000000000004 (BIGGER)
...
3.2 + 3.6 = 6.800000000000001 (BIGGER)
3.2 + 4.4 = 7.6000000000000005 (BIGGER)

При вычитании всех значений (a - b, где a> b) с шагом 0,1 (от 100 до 0,1) вероятность ошибки точности составляет ~34%. Вот некоторые примеры:

0.6 - 0.2 = 0.39999999999999997 (SMALLER)
0.5 - 0.4 = 0.09999999999999998 (SMALLER)
...
2.1 - 0.2 = 1.9000000000000001 (BIGGER)
2.0 - 1.9 = 0.10000000000000009 (BIGGER)
...
100 - 99.9 = 0.09999999999999432 (SMALLER)
100 - 99.8 = 0.20000000000000284 (BIGGER)

* 15% и 34% действительно огромны, поэтому всегда используйте BigDecimal, когда точность имеет большое значение. С двумя десятичными цифрами (шаг 0.01) ситуация ухудшается немного больше (18% и 36%).

31

Источник

user3294902 03 янв '15 в 12:12

Вы пробовали решение для клейкой ленты?

Попробуйте определить, когда возникают ошибки, и исправить их с помощью коротких операторов if, это не красиво, но для некоторых проблем это единственное решение, и это одно из них.

 if( (n * 0.1) < 100.0 ) { return n * 0.1 - 0.000000000000001 ;}
                    else { return n * 0.1 + 0.000000000000001 ;}

У меня была такая же проблема в проекте научного моделирования на C#, и я могу сказать вам, что если вы проигнорируете эффект бабочки, он превратится в большого толстого дракона и укусит вас в а **

19

Источник

user1336271 01 авг '12 в 07:02

Учитывая, что никто не упомянул об этом...

Некоторые языки высокого уровня, такие как Python и Java, поставляются с инструментами для преодоления двоичных ограничений с плавающей запятой. Например:

Питона decimal модуль и Java BigDecimal класс, который представляет числа внутри с десятичной записью (в отличие от двоичной записи). Оба имеют ограниченную точность, поэтому они все еще подвержены ошибкам, однако они решают наиболее распространенные проблемы с двоичной арифметикой с плавающей запятой.
Десятичные числа очень хороши при работе с деньгами: десять центов плюс двадцать центов всегда равны тридцати центам:
```
>>> 0.1 + 0.2 == 0.3
False
>>> Decimal('0.1') + Decimal('0.2') == Decimal('0.3')
True
```
Питона decimal Модуль основан на стандарте IEEE 854-1987.
Питона fractions модуль и Apache Common's BigFraction класс Оба представляют рациональные числа как (numerator, denominator) пары, и они могут дать более точные результаты, чем десятичная арифметика с плавающей запятой.

Ни одно из этих решений не является идеальным (особенно если мы посмотрим на производительность или если нам требуется очень высокая точность), но тем не менее они решают большое количество проблем с двоичной арифметикой с плавающей запятой.

19

Источник

user1913824 21 авг '15 в 14:53

Эти странные числа появляются потому, что компьютеры используют двоичную (основание 2) систему счисления для целей расчета, а мы используем десятичную (основание 10).

Существует большинство дробных чисел, которые не могут быть точно представлены ни в двоичном, ни в десятичном виде, ни в обоих. Результат - округленное (но точное) число результатов.

18

Источник

user1211623 14 окт '13 в 16:45

Могу ли я просто добавить; люди всегда считают, что это проблема с компьютером, но если вы считаете своими руками (база 10), вы не можете получить (1/3+1/3=2/3)=true если у вас нет бесконечности, чтобы добавить 0,333... до 0,333... так же, как с (1/10+2/10)!==3/10 проблема в базе 2, вы усекаете ее до 0,333 + 0,333 = 0,666 и, вероятно, округляете ее до 0,667, что также будет технически неточным.

Подсчитайте в троице, и трети не проблема - хотя, возможно, какая-то гонка с 15 пальцами на каждой руке спросит, почему ваша десятичная математика была нарушена...

18

Источник

18 мар '16 в 00:38

Многие из многочисленных дубликатов этого вопроса спрашивают о влиянии округления с плавающей запятой на конкретные числа. На практике легче понять, как это работает, рассматривая точные результаты вычислений, а не просто читая об этом. Некоторые языки предоставляют способы сделать это - например, преобразование float или же double в BigDecimal на Яве.

Поскольку это вопрос, не зависящий от языка, ему необходимы инструменты, не зависящие от языка, такие как преобразование десятичных чисел в числа с плавающей запятой.

Применяя его к числам в вопросе, рассматривается как двойное число:

0,1 преобразуется в 0,1000000000000000055511151231257827021181583404541015625,

0.2 преобразуется в 0.200000000000000011102230246251565404236316680908203125,

0,3 преобразуется в 0,299999999999999988897769753748434595763683319091796875 и

0.30000000000000004 преобразуется в 0.3000000000000000444089209850062616169452667236328125.

При добавлении первых двух чисел вручную или в десятичном калькуляторе, таком как Калькулятор полной точности, отображается точная сумма фактических входных значений, равная 0.3000000000000000166533453693773481063544750213623046875.

Если бы оно было округлено до эквивалента 0,3, ошибка округления была бы равна 0,0000000000000000277555756156289135105907917022705078125. Округление до эквивалента 0,30000000000000004 также дает ошибку округления 0,0000000000000000277555756156289135105907917022705078125. Действует прерыватель галстука от круглого к четному.

Возвращаясь к преобразователю с плавающей запятой, необработанный шестнадцатеричный код для 0.30000000000000004 равен 3fd3333333333334, который заканчивается четной цифрой и, следовательно, является правильным результатом.

17

Источник

user1798593 21 дек '15 в 11:15

Просто для забавы, я играл с представлением поплавков, следуя определениям из стандарта C99, и я написал код ниже.

Код печатает двоичное представление с плавающей точкой в 3 отдельных группах

SIGN EXPONENT FRACTION

и после этого он печатает сумму, которая при суммировании с достаточной точностью покажет значение, которое действительно существует в аппаратном обеспечении.

Поэтому, когда вы пишете float x = 999...компилятор преобразует это число в битовое представление, напечатанное функцией xx такая, что сумма выводится функцией yy быть равным данному числу.

На самом деле эта сумма только приблизительная. Для числа 999 999 999 компилятор вставит в битовое представление числа с плавающей точкой число 1 000 000 000

После кода я присоединяю консольный сеанс, в котором я вычисляю сумму терминов для обеих констант (минус PI и 999999999), которые действительно существуют в аппаратных средствах, вставленных туда компилятором.

#include <stdio.h>
#include <limits.h>

void
xx(float *x)
{
    unsigned char i = sizeof(*x)*CHAR_BIT-1;
    do {
        switch (i) {
        case 31:
             printf("sign:");
             break;
        case 30:
             printf("exponent:");
             break;
        case 23:
             printf("fraction:");
             break;

        }
        char b=(*(unsigned long long*)x&((unsigned long long)1<<i))!=0;
        printf("%d ", b);
    } while (i--);
    printf("\n");
}

void
yy(float a)
{
    int sign=!(*(unsigned long long*)&a&((unsigned long long)1<<31));
    int fraction = ((1<<23)-1)&(*(int*)&a);
    int exponent = (255&((*(int*)&a)>>23))-127;

    printf(sign?"positive" " ( 1+":"negative" " ( 1+");
    unsigned int i = 1<<22;
    unsigned int j = 1;
    do {
        char b=(fraction&i)!=0;
        b&&(printf("1/(%d) %c", 1<<j, (fraction&(i-1))?'+':')' ), 0);
    } while (j++, i>>=1);

    printf("*2^%d", exponent);
    printf("\n");
}

void
main()
{
    float x=-3.14;
    float y=999999999;
    printf("%lu\n", sizeof(x));
    xx(&x);
    xx(&y);
    yy(x);
    yy(y);
}

Вот сеанс консоли, в котором я вычисляю реальное значение числа с плавающей точкой, которое существует в аппаратных средствах. я использовал bc распечатать сумму слагаемых, выводимых основной программой. Можно вставить эту сумму в Python repl или что-то подобное тоже.

-- .../terra1/stub
@ qemacs f.c
-- .../terra1/stub
@ gcc f.c
-- .../terra1/stub
@ ./a.out
sign:1 exponent:1 0 0 0 0 0 0 fraction:0 1 0 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 1
sign:0 exponent:1 0 0 1 1 1 0 fraction:0 1 1 0 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0
negative ( 1+1/(2) +1/(16) +1/(256) +1/(512) +1/(1024) +1/(2048) +1/(8192) +1/(32768) +1/(65536) +1/(131072) +1/(4194304) +1/(8388608) )*2^1
positive ( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
-- .../terra1/stub
@ bc
scale=15
( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
999999999.999999446351872

Вот и все. Значение 999999999 на самом деле

999999999.999999446351872

Вы также можете проверить с bc что -3.14 тоже возмущено. Не забудьте установить scale фактор в bc,

Отображаемая сумма - это то, что находится внутри оборудования. Значение, которое вы получаете, вычисляя его, зависит от установленного вами масштаба. Я установил scale множитель до 15. Математически, с бесконечной точностью, кажется, что это 1 000 000 000.

10

Источник

user1419272 29 дек '16 в 10:29

Тип математики с плавающей точкой, который может быть реализован в цифровом компьютере, обязательно использует аппроксимацию действительных чисел и операций с ними. (Стандартная версия содержит более пятидесяти страниц документации и имеет комитет, который занимается ее ошибками и дальнейшей доработкой.)

Это приближение представляет собой смесь приближений разных видов, каждое из которых может либо игнорироваться, либо тщательно учитываться из-за своего специфического способа отклонения от точности. Это также включает ряд явных исключительных случаев как на аппаратном, так и на программном уровне, которые большинство людей проходят мимо, делая вид, что не замечают.

Если вам нужна бесконечная точность (например, с использованием числа π вместо одного из многих его более коротких заменителей), вам следует написать или использовать символическую математическую программу.

Но если вы согласны с идеей, что иногда математика с плавающей запятой нечеткая по значению, а логика и ошибки могут быстро накапливаться, и вы можете написать свои требования и тесты, чтобы учесть это, тогда ваш код часто может обойтись тем, что в ваш FPU.

10

Источник

user5391501 05 окт '15 в 15:55

Числа с плавающей запятой представляются на аппаратном уровне как дроби двоичных чисел (основание 2). Например, десятичная дробь:

0.125

имеет значение 1/10 + 2/100 + 5/1000 и, таким же образом, двоичную дробь:

0.001

имеет значение 0/2 + 0/4 + 1/8. Эти две дроби имеют одинаковое значение, с той лишь разницей, что первая - десятичная дробь, вторая - двоичная.

К сожалению, большинство десятичных дробей не могут иметь точного представления в двоичных дробях. Поэтому, как правило, числа с плавающей запятой, которые вы даете, только аппроксимируются до двоичных дробей, которые хранятся в машине.

К задаче проще подойти в базе 10. Возьмем, например, дробь 1/3. Вы можете округлить его до десятичной дроби:

0.3

или лучше,

0.33

или лучше,

0.333

и т.д. Независимо от того, сколько десятичных знаков вы напишете, результат никогда не будет точно 1/3, но это оценка, которая всегда приближается.

Аналогичным образом, независимо от того, сколько десятичных знаков с основанием 2 вы используете, десятичное значение 0,1 не может быть представлено точно как двоичная дробь. В базе 2 1/10 - это периодическое число:

0.0001100110011001100110011001100110011001100110011 ...

Остановитесь на любом конечном количестве бит, и вы получите приближение.

Для Python на типичной машине 53 бита используются для точности числа с плавающей запятой, поэтому значение, сохраненное при вводе десятичной дроби 0,1, является двоичной дробью.

0.00011001100110011001100110011001100110011001100110011010

что близко, но не совсем равно 1/10.

Легко забыть, что сохраненное значение является приближением исходной десятичной дроби из-за того, как числа с плавающей запятой отображаются в интерпретаторе. Python отображает только десятичное приближение значения, хранящегося в двоичном формате. Если бы Python выводил истинное десятичное значение двоичного приближения, сохраненного для 0,1, он бы выводил:

>>> 0.1
0.1000000000000000055511151231257827021181583404541015625

Это намного больше десятичных знаков, чем ожидает большинство людей, поэтому Python отображает округленное значение для улучшения читаемости:

>>> 0.1
0.1

Важно понимать, что на самом деле это иллюзия: сохраненное значение не совсем 1/10, просто на дисплее сохраненное значение округляется. Это становится очевидным, как только вы выполняете арифметические операции с этими значениями:

>>> 0.1 + 0.2
0.30000000000000004

Такое поведение присуще самой природе представления машины с плавающей запятой: это не ошибка в Python и не ошибка в вашем коде. Вы можете наблюдать тот же тип поведения на всех других языках, которые используют аппаратную поддержку для вычисления чисел с плавающей запятой (хотя некоторые языки не делают разницу видимой по умолчанию или не во всех режимах отображения).

В этом есть еще один сюрприз. Например, если вы попытаетесь округлить значение 2,675 до двух десятичных знаков, вы получите

>>> round (2.675, 2)
2.67

В документации примитива round() указано, что он округляется до ближайшего значения, отличного от нуля. Поскольку десятичная дробь находится на полпути между 2,67 и 2,68, вы должны ожидать получить (двоичное приближение) 2,68. Однако это не так, потому что, когда десятичная дробь 2,675 преобразуется в число с плавающей запятой, она сохраняется в приближении, точное значение которого:

2.67499999999999982236431605997495353221893310546875

Поскольку аппроксимация немного ближе к 2,67, чем к 2,68, округление меньше.

Если вы находитесь в ситуации, когда округление десятичных чисел наполовину имеет значение, вам следует использовать модуль decimal. Кстати, модуль decimal также предоставляет удобный способ "увидеть" точное значение, сохраненное для любого числа с плавающей запятой.

>>> from decimal import Decimal
>>> Decimal (2.675)
>>> Decimal ('2.67499999999999982236431605997495353221893310546875')

Другим следствием того факта, что 0,1 не точно сохраняется в 1/10, является то, что сумма десяти значений 0,1 также не дает 1,0:

>>> sum = 0.0
>>> for i in range (10):
... sum + = 0.1
...>>> sum
0.9999999999999999

Арифметика двоичных чисел с плавающей запятой таит много таких сюрпризов. Проблема с "0.1" подробно объясняется ниже, в разделе "Ошибки представления". См. "Опасности с плавающей точкой" для более полного списка таких сюрпризов.

Это правда, что нет простого ответа, но не стоит слишком подозревать плавающие виртуальные числа! Ошибки в Python при операциях с числами с плавающей запятой связаны с лежащим в основе оборудованием, и на большинстве машин не более 1 из 2 ** 53 на операцию. Это более чем необходимо для большинства задач, но вы должны помнить, что это не десятичные операции, и каждая операция с числами с плавающей запятой может иметь новую ошибку.

Хотя существуют патологические случаи, для наиболее распространенных вариантов использования вы получите ожидаемый результат в конце, просто округлив в большую сторону до количества десятичных знаков, которое вы хотите отобразить на дисплее. Для точного управления тем, как отображаются числа с плавающей запятой, см. Синтаксис форматирования строки для спецификаций форматирования метода str.format ().

В этой части ответа подробно объясняется пример "0.1" и показано, как вы можете самостоятельно провести точный анализ этого типа кейса. Мы предполагаем, что вы знакомы с двоичным представлением чисел с плавающей запятой. Термин Ошибка представления означает, что большинство десятичных дробей не могут быть представлены точно в двоичном формате. Это основная причина, по которой Python (или Perl, C, C ++, Java, Fortran и многие другие) обычно не отображает точный результат в десятичном виде:

>>> 0.1 + 0.2
0.30000000000000004

Почему? 1/10 и 2/10 не могут быть представлены точно в двоичных дробях. Однако все машины сегодня (июль 2010 г.) следуют стандарту IEEE-754 для арифметики чисел с плавающей запятой. и большинство платформ используют "двойную точность IEEE-754" для представления Python с плавающей точкой. Двойная точность IEEE-754 использует 53 бита точности, поэтому при чтении компьютер пытается преобразовать 0,1 в ближайшую дробь формы J / 2 ** N, где J - целое число, равное ровно 53 битам. Перепишите:

1/10 ~ = J / (2 ** N)

в:

J ~ = 2 ** N / 10

помня, что J составляет ровно 53 бита (поэтому> = 2 ** 52, но <2 ** 53), наилучшее возможное значение для N - 56:

>>> 2 ** 52
4503599627370496
>>> 2 ** 53
9007199254740992
>>> 2 ** 56/10
7205759403792793

Итак, 56 - единственное возможное значение для N, которое оставляет ровно 53 бита для J. Таким образом, наилучшее возможное значение для J - это частное, округленное:

>>> q, r = divmod (2 ** 56, 10)
>>> r
6

Поскольку перенос больше половины 10, наилучшее приближение получается округлением в большую сторону:

>>> q + 1
7205759403792794

Поэтому наилучшее возможное приближение для 1/10 в "двойной точности IEEE-754" - это выше 2 ** 56, то есть:

7205759403792794/72057594037927936

Обратите внимание, что, поскольку округление было выполнено в большую сторону, результат на самом деле немного больше 1/10; если бы мы не округляли в большую сторону, частное было бы чуть меньше 1/10. Но ни в коем случае не 1/10!

Таким образом, компьютер никогда не "видит" 1/10: он видит точную дробь, указанную выше, наилучшее приближение с использованием чисел с плавающей запятой двойной точности из "" IEEE-754 ":

>>>. 1 * 2 ** 56
7205759403792794.0

Если мы умножим эту дробь на 10 ** 30, мы сможем увидеть значения ее 30 десятичных знаков сильного веса.

>>> 7205759403792794 * 10 ** 30 // 2 ** 56
100000000000000005551115123125L

Это означает, что точное значение, хранящееся в компьютере, примерно равно десятичному значению 0,100000000000000005551115123125. В версиях до Python 2.7 и Python 3.1 Python округлял эти значения до 17 значащих десятичных знаков, отображая "0,10000000000000001". В текущих версиях Python отображаемое значение - это значение, дробная часть которого является как можно короче, но дает точно такое же представление при преобразовании обратно в двоичное, просто отображая "0,1".

9

Источник

user13211997 03 авг '20 в 18:03

Sine Python 3.5 вы можете использовать math.isclose() функционировать в условиях

import math

if math.isclose(0.1 + 0.2, 0.3, abs_tol=0.01):
    pass

9

Источник

user5263977 08 авг '18 в 08:47

Ловушка с числами с плавающей запятой заключается в том, что они выглядят как десятичные, но работают в двоичном формате.

Единственный простой множитель 2 - 2, в то время как 10 имеет простые множители 2 и 5. В результате каждое число, которое может быть записано точно как двоичная дробь, также может быть записано точно как десятичная дробь, но только подмножество десятичные числа.

Число с плавающей запятой - это, по сути, двоичная дробь с ограниченным количеством значащих цифр. Если вы пропустите эти значащие цифры, результаты будут округлены.

Когда вы вводите литерал в свой код или вызываете функцию для синтаксического анализа числа с плавающей запятой в строку, он ожидает десятичное число и сохраняет двоичное приближение этого десятичного числа в переменной.

Когда вы печатаете число с плавающей запятой или вызываете функцию для преобразования одного в строку, она печатает десятичное приближение числа с плавающей запятой. Это является возможным преобразовать двоичное число в десятичное точно, но ни один язык я знаю не делает это по умолчанию. В некоторых языках используется фиксированное количество десятичных знаков, в других - самая короткая строка, возвращающая в оба конца то же самое значение с плавающей запятой.

9

Источник

user5083516 16 сен '21 в 03:28

Другой способ взглянуть на это: используются 64 бита для представления чисел. Как следствие, не существует более 2**64 = 18 446 744 073 709 551 616 различных чисел, которые могут быть точно представлены.

Тем не менее, Мат говорит, что между 0 и 1 уже существует бесконечно много десятичных знаков. IEE 754 определяет кодировку для эффективного использования этих 64 битов для гораздо большего числового пространства плюс NaN и +/- Infinity, поэтому между точно представленными числами, заполненными числа только приблизительные.

К сожалению, 0,3 сидит в пробел.

7

Источник

user515069 19 дек '17 в 22:37

Десятичные дроби, такие как 0.1, 0.2 а также 0.3 не представлены точно в двоично-закодированных типах с плавающей точкой. Сумма аппроксимаций для 0.1 а также 0.2 отличается от приближения, используемого для 0.3отсюда ложь 0.1 + 0.2 == 0.3 как можно увидеть здесь более четко:

#include <stdio.h>

int main() {
    printf("0.1 + 0.2 == 0.3 is %s\n", 0.1 + 0.2 == 0.3 ? "true" : "false");
    printf("0.1 is %.23f\n", 0.1);
    printf("0.2 is %.23f\n", 0.2);
    printf("0.1 + 0.2 is %.23f\n", 0.1 + 0.2);
    printf("0.3 is %.23f\n", 0.3);
    printf("0.3 - (0.1 + 0.2) is %g\n", 0.3 - (0.1 + 0.2));
    return 0;
}

Выход:

0.1 + 0.2 == 0.3 is false
0.1 is 0.10000000000000000555112
0.2 is 0.20000000000000001110223
0.1 + 0.2 is 0.30000000000000004440892
0.3 is 0.29999999999999998889777
0.3 - (0.1 + 0.2) is -5.55112e-17

Чтобы эти вычисления были оценены более надежно, вам необходимо использовать десятичное представление для значений с плавающей запятой. Стандарт C не определяет такие типы по умолчанию, но как расширение, описанное в Техническом отчете. Типы _Decimal32, _Decimal64 а также _Decimal128 может быть доступно в вашей системе (например, gcc поддерживает их по выбранным целям, но clang не поддерживает их в OS/X).

5

Источник

user4593267 22 апр '19 в 01:02

Это на самом деле довольно просто. Когда у вас есть система 10-й базы (как наша), она может выражать только дроби, которые используют основной множитель базы. Первичные множители 10 равны 2 и 5. Таким образом, 1/2, 1/4, 1/5, 1/8 и 1/10 могут быть выражены чисто, потому что все знаменатели используют простые множители 10. Напротив, 1/3, 1/6 и 1/7 - все повторяющиеся десятичные дроби, потому что их знаменатели используют простой множитель 3 или 7. В двоичном (или базовом 2) единственном простом множителе является 2. Таким образом, вы можете выражать только те дроби, которые содержат только 2 как главный фактор. В двоичном коде 1/2, 1/4, 1/8 все будет выражено чисто в десятичном виде. В то время как 1/5 или 1/10 будут повторять десятичные дроби. Таким образом, 0,1 и 0,2 (1/10 и 1/5), в то время как чистые десятичные дроби в системе Base 10, являются повторяющимися десятичными знаками в системе Base 2, в которой работает компьютер. Когда вы выполняете математику с этими повторяющимися десятичными знаками, вы получаете остатки которые переносятся, когда вы конвертируете двоичное (двоичное) число компьютера в более удобочитаемое число 10.

С https://0.30000000000000004.com/

5

Источник

user5012228 07 май '19 в 19:45

Представьте, что вы работаете в базовой десятке, скажем, с 8 цифрами точности. Вы проверяете,

1/3 + 2 / 3 == 1

и узнайте, что это возвращается false, Зачем? Ну, а реальные цифры у нас есть

1/3 = 0,333.... и 2/3 = 0,666....

Обрезая в восемь знаков после запятой, мы получаем

0.33333333 + 0.66666666 = 0.99999999

что, конечно, отличается от 1.00000000 точно 0.00000001,

Ситуация для двоичных чисел с фиксированным числом битов в точности аналогична. Как реальные цифры, мы имеем

1/10 = 0,0001100110011001100... (база 2)

а также

1/5 = 0,0011001100110011001... (база 2)

Если бы мы урезали их, скажем, до семи бит, то мы бы получили

0.0001100 + 0.0011001 = 0.0100101

в то время как с другой стороны,

3/10 = 0,01001100110011... (база 2)

который, усеченный до семи бит, 0.0100110и они отличаются точно 0.0000001,

Точная ситуация немного сложнее, потому что эти цифры обычно хранятся в научной записи. Так, например, вместо того, чтобы хранить 1/10 как 0.0001100 мы можем хранить это как что-то вроде 1.10011 * 2^-4в зависимости от того, сколько битов мы выделили для экспоненты и мантиссы. Это влияет на то, сколько цифр вы получите для своих расчетов.

В результате из-за этих ошибок округления вы, по сути, никогда не захотите использовать == для чисел с плавающей запятой. Вместо этого вы можете проверить, меньше ли абсолютное значение их разности, чем некоторое фиксированное небольшое число.

5

Источник

user2462437 20 дек '18 в 18:27

Обычная арифметика - это основание 10, поэтому десятичные дроби представляют десятые, сотые и т. Д. Когда вы пытаетесь представить число с плавающей запятой в двоичной арифметике с основанием 2, вы имеете дело с половинами, четвертями, восьмыми и т. Д.

В аппаратном обеспечении числа с плавающей запятой хранятся как целые мантиссы и экспоненты. Мантисса представляет собой значащие цифры. Экспонента похожа на научную запись, но в ней используется основание 2 вместо 10. Например, 64,0 будет представлено мантиссой 1 и показателем 6. 0,125 будет представлено мантиссой 1 и показателем -3.

Десятичные дроби с плавающей запятой должны складывать отрицательные степени двойки.

0.1b = 0.5d
0.01b = 0.25d
0.001b = 0.125d
0.0001b = 0.0625d
0.00001b = 0.03125d

и так далее.

При работе с арифметикой с плавающей запятой обычно используется дельта ошибок вместо операторов равенства. Вместо того

if(a==b) ...

вы бы использовали

delta = 0.0001; // or some arbitrarily small amount
if(a - b > -delta && a - b < delta) ...

4

Источник

user10039698 20 авг '20 в 18:38

Поскольку этот поток немного расширился до общего обсуждения текущих реализаций с плавающей запятой, я бы добавил, что существуют проекты по устранению их проблем.

Взгляните, например, на https://posithub.org/, который демонстрирует тип числа, называемый posit (и его предшественник unum), который обещает предложить лучшую точность с меньшим количеством битов. Если мое понимание верно, это также устраняет проблемы в этом вопросе. Довольно интересный проект, за ним стоит математик доктор Джон Густафсон. Все это с открытым исходным кодом, со многими актуальными реализациями на C/C++, Python, Julia и C# ( https://hastlayer.com/arithmetics).

4

Источник

user220230 22 дек '17 в 16:39

Другие вопросы по тегам math floating-point language-agnostic floating-accuracy

user3153 25 фев '09 в 21:40 2009-02-25 21:40 · Accepted Answer · 2009-02-25 21:40

Двоичная математика с плавающей запятой такая. В большинстве языков программирования он основан на стандарте IEEE 754. JavaScript использует 64-битное представление с плавающей запятой, такое же как в Java double, Суть проблемы заключается в том, что числа представлены в этом формате как целое число, умноженное на два; рациональные числа (такие как 0.1, который 1/10) знаменатель которого не является степенью двойки, не может быть точно представлен.

За 0.1 в стандарте binary64 формат, представление может быть записано точно так же, как

0.1000000000000000055511151231257827021181583404541015625 в десятичном или
0x1.999999999999ap-4 в шестнадцатеричном формате С99

В отличие от рационального числа 0.1, который 1/10, можно записать точно так же, как

0.1 в десятичном или
0x1.99999999999999...p-4 в аналоге гексафлотной записи С99, где ... представляет бесконечную последовательность 9-х.

Константы 0.2 а также 0.3 в вашей программе также будут приближения к их истинным значениям. Бывает, что ближайший double в 0.2 больше рационального числа 0.2 но что ближе всего double в 0.3 меньше рационального числа 0.3, Сумма 0.1 а также 0.2 получается больше рационального числа 0.3 и, следовательно, не согласен с константой в вашем коде.

Достаточно всеобъемлющее рассмотрение арифметических задач с плавающей запятой - это то, что должен знать каждый компьютерный специалист об арифметике с плавающей запятой. Для более легкого для понимания объяснения, см. Плавающую точку- gui.de.