Можно ли объяснить разницу между кубитом и битом на простом примере кода?

Question

Единственные места, где я знаю, что вы можете играть с квантовыми вычислениями, - это квантовая площадка Google и квантовый опыт IBM. В то время как первый использует языки qscript и второй язык qasm (которые легко изучаются), их использование по-прежнему не сильно отличается от обычного программирования (за исключением нескольких специфических функций). Вот объяснение Википедии:

Кубит имеет несколько сходств с классическим битом, но в целом сильно отличается. Существует два возможных результата измерения кубита - обычно 0 и 1, например, бит. Разница заключается в том, что, хотя состояние бита равно 0 или 1, состояние кубита также может быть суперпозицией обоих. Возможно полное кодирование одного бита в одном кубите. Однако кубит может содержать даже больше информации, например, до двух битов с использованием сверхплотного кодирования.

Для системы из n компонентов полное описание ее состояния в классической физике требует только n битов, тогда как в квантовой физике требуется 2^n - 1 комплексных чисел.

Что более-менее понятно. Но как это можно показать на примере кода?

Answer 1

Вот некоторый классический код, который подбрасывает монеты и подсчитывает, сколько у вас голов:

def coin_count():
    bit = False
    counter = 0
    for _ in range(500):
        bit ^= random() < 0.5  # False → 50% False, 50% True
                               #  True → 50% False, 50% True
        if bit:
            counter += 1
    return counter

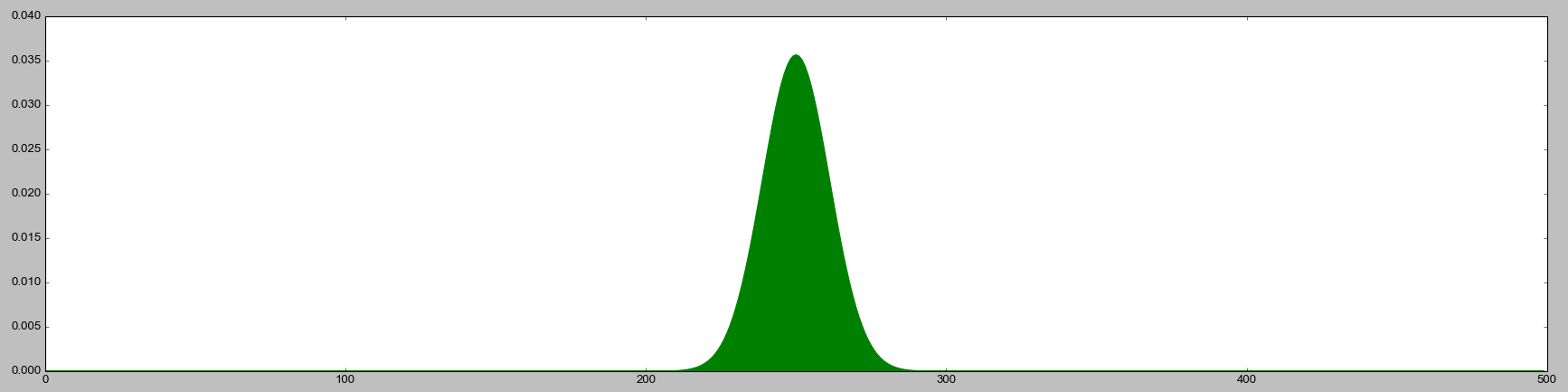
Если вы запустите этот код много раз и создадите гистограмму, результатом будет примерно биномиальное распределение:

Теперь приведем некоторый псевдокод, который делает то же самое, за исключением того, что монета заменена кубитом. Мы "переворачиваем кубит", применяя к нему операцию Адамара.

def hadamard_coin_count():
    qubit = qalloc()
    counter = 0
    for _ in range(500):
        apply Hadamard to qubit # |0⟩ → √½|0⟩ + √½|1⟩
                                # |1⟩ → √½|0⟩ - √½|1⟩
        if qubit:  # (not a measurement; controls nested operations)
            counter += 1  # (happens only in some parts of the superposition)
    return measure(counter)  # (note: counter was in superposition)

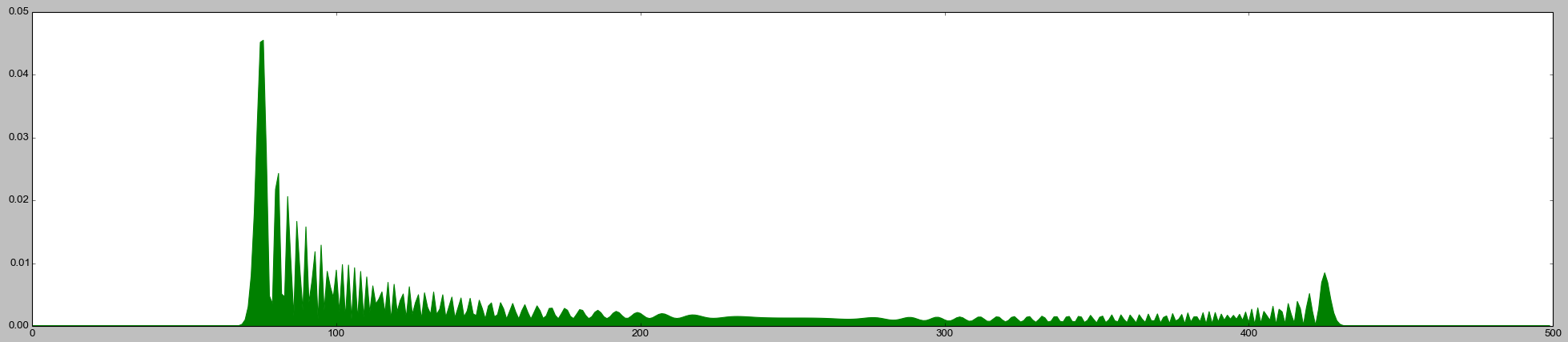
Сделайте это много раз, постройте распределение, и вы получите что-то совсем другое:

Очевидно, что эти фрагменты кода делают совершенно разные вещи, несмотря на их поверхностное сходство. Квантовые прогулки не действуют так же, как классические случайные прогулки. Эта разница полезна в некоторых алгоритмах.