Как бороться с точностью чисел с плавающей точкой в JavaScript?
У меня есть следующий тестовый скрипт:
function test(){
var x = 0.1 * 0.2;
document.write(x);
}
test();
Это напечатает результат 0.020000000000000004 в то время как это должно просто напечатать 0.02 (если вы используете свой калькулятор). Насколько я понял, это связано с ошибками в точности умножения с плавающей точкой.
У кого-нибудь есть хорошее решение, чтобы в таком случае я получил правильный результат 0.02? Я знаю, что есть такие функции, как toFixed или округление было бы другой возможностью, но я бы хотел, чтобы на самом деле было напечатано целое число без каких-либо вырезок и округлений Просто хотел узнать, есть ли у кого-нибудь хорошее, элегантное решение.
Конечно, иначе я округлю до 10 цифр или около того.
49 ответов
Из путеводителя с плавающей точкой:
Что я могу сделать, чтобы избежать этой проблемы?
Это зависит от того, какие вычисления вы делаете.
- Если вам действительно нужно, чтобы ваши результаты точно суммировались, особенно когда вы работаете с деньгами: используйте специальный десятичный тип данных.
- Если вы просто не хотите видеть все эти дополнительные десятичные разряды: просто отформатируйте результат, округленный до фиксированного количества десятичных разрядов, при его отображении.
- Если у вас нет доступного десятичного типа данных, альтернативой является работа с целыми числами, например, производите денежные вычисления полностью в центах. Но это больше работы и имеет некоторые недостатки.
Обратите внимание, что первый пункт применяется только в том случае, если вам действительно нужно конкретное точное десятичное поведение. Большинству людей это не нужно, они просто раздражены тем, что их программы не работают правильно с числами, такими как 1/10, даже не осознавая, что они даже не будут мигать при той же ошибке, если она произошла с 1/3.
Если первая точка зрения действительно применима к вам, используйте BigDecimal для JavaScript, который совсем не элегантен, но фактически решает проблему, а не предоставляет несовершенный обходной путь.
Мне нравится решение Педро Ладарии и я использую что-то подобное.
function strip(number) {
return (parseFloat(number).toPrecision(12));
}
В отличие от решения Pedros, оно округляется до 0,999... повторяется и с точностью до плюс / минус один на младшей значащей цифре.
Примечание. При работе с 32- или 64-разрядными числами с плавающей запятой следует использовать toPrecision(7) и toPrecision(15) для достижения наилучших результатов. Смотрите этот вопрос для информации о том, почему.
Для математически склонных: http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
Рекомендуемый подход заключается в использовании поправочных коэффициентов (умножьте на подходящую степень 10, чтобы арифметика происходила между целыми числами). Например, в случае 0.1 * 0.2поправочный коэффициент 10и вы выполняете расчет:
> var x = 0.1
> var y = 0.2
> var cf = 10
> x * y
0.020000000000000004
> (x * cf) * (y * cf) / (cf * cf)
0.02
(Очень быстрое) решение выглядит примерно так:
var _cf = (function() {
function _shift(x) {
var parts = x.toString().split('.');
return (parts.length < 2) ? 1 : Math.pow(10, parts[1].length);
}
return function() {
return Array.prototype.reduce.call(arguments, function (prev, next) { return prev === undefined || next === undefined ? undefined : Math.max(prev, _shift (next)); }, -Infinity);
};
})();
Math.a = function () {
var f = _cf.apply(null, arguments); if(f === undefined) return undefined;
function cb(x, y, i, o) { return x + f * y; }
return Array.prototype.reduce.call(arguments, cb, 0) / f;
};
Math.s = function (l,r) { var f = _cf(l,r); return (l * f - r * f) / f; };
Math.m = function () {
var f = _cf.apply(null, arguments);
function cb(x, y, i, o) { return (x*f) * (y*f) / (f * f); }
return Array.prototype.reduce.call(arguments, cb, 1);
};
Math.d = function (l,r) { var f = _cf(l,r); return (l * f) / (r * f); };
В этом случае:
> Math.m(0.1, 0.2)
0.02
Я определенно рекомендую использовать проверенную библиотеку, такую как SinfulJS
Вы только выполняете умножение? Если это так, то вы можете использовать в своих интересах секрет секретной десятичной арифметики. Вот это NumberOfDecimals(X) + NumberOfDecimals(Y) = ExpectedNumberOfDecimals, То есть, если у нас есть 0.123 * 0.12 тогда мы знаем, что будет 5 знаков после запятой, потому что 0.123 имеет 3 знака после запятой и 0.12 имеет два Таким образом, если JavaScript дал нам число, подобное 0.014760000002 мы можем безопасно округлить до 5-го знака после запятой, не боясь потерять точность.
Удивительно, но эта функция еще не была опубликована, хотя у других есть похожие варианты. Это из веб-документов MDN для Math.round(). Это сжато и допускает переменную точность.
function precisionRound(number, precision) {
var factor = Math.pow(10, precision);
return Math.round(number * factor) / factor;
}
console.log (precisionRound (1234.5678, 1)); // ожидаемый результат: 1234.6
console.log (precisionRound (1234.5678, -1)); // ожидаемый результат: 1230
var inp = document.querySelectorAll('input');
var btn = document.querySelector('button');
btn.onclick = function(){
inp[2].value = precisionRound( parseFloat(inp[0].value) * parseFloat(inp[1].value) , 5 );
};
//MDN function
function precisionRound(number, precision) {
var factor = Math.pow(10, precision);
return Math.round(number * factor) / factor;
}button{
display: block;
}<input type='text' value='0.1'>
<input type='text' value='0.2'>
<button>Get Product</button>
<input type='text'>Я считаю, что BigNumber.js отвечает моим потребностям.
Библиотека JavaScript для десятичной и недесятичной арифметики произвольной точности.
У него хорошая документация, и автор очень старательно реагирует на отзывы.
Этот же автор имеет 2 другие похожие библиотеки:
Небольшая, быстрая библиотека JavaScript для десятичной арифметики произвольной точности. Младшая сестра bignumber.js.
Десятичный тип произвольной точности для JavaScript.
Вот код, использующий BigNumber:
$(function(){
var product = BigNumber(.1).times(.2);
$('#product').text(product);
var sum = BigNumber(.1).plus(.2);
$('#sum').text(sum);
});<script src="https://ajax.googleapis.com/ajax/libs/jquery/1.11.1/jquery.min.js"></script>
<!-- 1.4.1 is not the current version, but works for this example. -->
<script src="http://cdn.bootcss.com/bignumber.js/1.4.1/bignumber.min.js"></script>
.1 × .2 = <span id="product"></span><br>
.1 + .2 = <span id="sum"></span><br>Вы ищете sprintf реализация для JavaScript, так что вы можете записывать плавающие с небольшими ошибками в них (так как они хранятся в двоичном формате) в формате, который вы ожидаете.
Попробуйте javascript-sprintf, вы бы назвали это так:
var yourString = sprintf("%.2f", yourNumber);
распечатать ваш номер как число с двумя десятичными знаками.
Вы также можете использовать Number.toFixed() для отображения, если вы не хотите включать больше файлов просто для округления с плавающей запятой с заданной точностью.
var times = function (a, b) {
return Math.round((a * b) * 100)/100;
};
---или же---
var fpFix = function (n) {
return Math.round(n * 100)/100;
};
fpFix(0.1*0.2); // -> 0.02
---также---
var fpArithmetic = function (op, x, y) {
var n = {
'*': x * y,
'-': x - y,
'+': x + y,
'/': x / y
}[op];
return Math.round(n * 100)/100;
};
--- как в ---
fpArithmetic('*', 0.1, 0.2);
// 0.02
fpArithmetic('+', 0.1, 0.2);
// 0.3
fpArithmetic('-', 0.1, 0.2);
// -0.1
fpArithmetic('/', 0.2, 0.1);
// 2
Ты можешь использовать parseFloat() а также toFixed() если вы хотите обойти эту проблему для небольшой операции:
a = 0.1;
b = 0.2;
a + b = 0.30000000000000004;
c = parseFloat((a+b).toFixed(2));
c = 0.3;
a = 0.3;
b = 0.2;
a - b = 0.09999999999999998;
c = parseFloat((a-b).toFixed(2));
c = 0.1;
Эта функция будет определять необходимую точность по умножению двух чисел с плавающей запятой и возвращать результат с соответствующей точностью. Элегантно, хотя это не так.
function multFloats(a,b){
var atens = Math.pow(10,String(a).length - String(a).indexOf('.') - 1),
btens = Math.pow(10,String(b).length - String(b).indexOf('.') - 1);
return (a * atens) * (b * btens) / (atens * btens);
}
Вы просто должны решить, сколько десятичных цифр вы на самом деле хотите - не можете съесть торт и съесть его тоже:-)
Числовые ошибки накапливаются при каждой последующей операции, и если вы не отрежете ее раньше, она будет только расти. Числовые библиотеки, которые представляют результаты, которые выглядят чистыми, просто обрезают последние 2 цифры на каждом шаге, числовые сопроцессоры также имеют "нормальную" и "полную" длину по той же причине. Отрезки являются дешевыми для процессора, но очень дорогими для вас в сценарии (умножение и деление и использование pov(...)). Хорошая математическая библиотека предоставит слово (x,n), чтобы сделать отсечение для вас.
Так что по крайней мере вы должны сделать глобальную переменную / константу с помощью pov(10,n) - это означает, что вы определились с точностью, которая вам нужна:-) Затем выполните:
Math.floor(x*PREC_LIM)/PREC_LIM // floor - you are cutting off, not rounding
Вы также можете продолжать делать математику и только обрезать в конце - при условии, что вы только отображаете, а не делаете if-s с результатами. Если вы можете сделать это, тогда.toFixed (...) может быть более эффективным.
Если вы делаете сравнения if-s / и не хотите сокращать их, вам также нужна небольшая константа, обычно называемая eps, которая на один десятичный знак выше максимальной ожидаемой ошибки. Скажем, что ваш предел составляет последние два знака после запятой - тогда ваш eps имеет 1 на 3-м месте от последнего (3-е наименее значимое), и вы можете использовать его, чтобы сравнить, находится ли результат в пределах ожидаемого диапазона eps (0,02 -eps < 0,1) *0,2 < 0,02 + EPS).
Обратите внимание, что для общего назначения такое поведение, вероятно, будет приемлемым.
Проблема возникает при сравнении этих значений с плавающей запятой, чтобы определить соответствующее действие.
С появлением ES6, новая константа Number.EPSILON определяется для определения допустимой погрешности:
Таким образом, вместо выполнения сравнения, как это
0.1 + 0.2 === 0.3 // which returns false
Вы можете определить пользовательскую функцию сравнения, например так:
function epsEqu(x, y) {
return Math.abs(x - y) < Number.EPSILON;
}
console.log(epsEqu(0.1+0.2, 0.3)); // true
decimal.js, big.js или bignumber.js могут быть использованы, чтобы избежать проблем манипуляции с плавающей точкой в Javascript:
0.1 * 0.2 // 0.020000000000000004
x = new Decimal(0.1)
y = x.times(0.2) // '0.2'
x.times(0.2).equals(0.2) // true
big.js: минималистский; легко использовать; точность указана в десятичных разрядах; Точность применяется только к делению.
bignumber.js: базы 2-64; варианты конфигурации; NaN; бесконечность; точность указана в десятичных разрядах; точность применяется только к делению; базовые префиксы.
decimal.js: базы 2-64; варианты конфигурации; NaN; бесконечность; нецелые степени, exp, ln, log; точность указана в значащих цифрах; точность всегда применяется; случайные числа.
Результат, который вы получили, является правильным и достаточно согласованным для реализаций с плавающей запятой на разных языках, процессорах и операционных системах - единственное, что изменяется, это уровень погрешности, когда число с плавающей запятой на самом деле удваивается (или выше).
0,1 в двоичных числах с плавающей запятой - как 1/3 в десятичной (т. Е. 0,3333333333333... навсегда), точного способа справиться с этим просто нет.
Если вы имеете дело с числами с плавающей запятой, всегда ожидайте небольших ошибок округления, поэтому вам также всегда придется округлять отображаемый результат до чего-то разумного. Взамен вы получаете очень очень быструю и мощную арифметику, потому что все вычисления находятся в собственном двоичном коде процессора.
В большинстве случаев решение состоит не в том, чтобы переключаться на арифметику с фиксированной запятой, главным образом потому, что она намного медленнее и в 99% случаев вам просто не нужна точность. Если вы имеете дело с вещами, которым нужен такой уровень точности (например, финансовые транзакции), Javascript, вероятно, не лучший инструмент для использования в любом случае (так как вы хотите применять типы с фиксированной запятой, статический язык, вероятно, лучше).
Вы ищете элегантное решение, тогда я боюсь, что это оно и есть: поплавки быстрые, но с небольшими ошибками округления - всегда округляют до чего-то разумного при отображении своих результатов.
Функция round() на phpjs.org работает хорошо: http://phpjs.org/functions/round
num = .01 + .06; // yields 0.0699999999999
rnum = round(num,12); // yields 0.07
0.6 * 3 это круто!)) Для меня это отлично работает
function dec( num )
{
var p = 100;
return Math.round( num * p ) / p;
}
Очень очень просто))
Решил это, сначала сделав оба числа целыми, выполнив выражение и затем разделив результат, чтобы вернуть десятичные разряды:
function evalMathematicalExpression(a, b, op) {
const smallest = String(a < b ? a : b);
const factor = smallest.length - smallest.indexOf('.');
for (let i = 0; i < factor; i++) {
b *= 10;
a *= 10;
}
a = Math.round(a);
b = Math.round(b);
const m = 10 ** factor;
switch (op) {
case '+':
return (a + b) / m;
case '-':
return (a - b) / m;
case '*':
return (a * b) / (m ** 2);
case '/':
return a / b;
}
throw `Unknown operator ${op}`;
}
Результаты для нескольких операций (исключенные числа являются результатами eval):
0.1 + 0.002 = 0.102 (0.10200000000000001)
53 + 1000 = 1053 (1053)
0.1 - 0.3 = -0.2 (-0.19999999999999998)
53 - -1000 = 1053 (1053)
0.3 * 0.0003 = 0.00009 (0.00008999999999999999)
100 * 25 = 2500 (2500)
0.9 / 0.03 = 30 (30.000000000000004)
100 / 50 = 2 (2)
Чтобы избежать этого, вы должны работать с целочисленными значениями, а не с плавающей точкой. Поэтому, когда вы хотите иметь точность в 2 позиции, работайте со значениями * 100, для 3 позиций используйте 1000. При отображении вы используете форматер, чтобы вставить разделитель.
Многие системы опускают работу с десятичными числами таким образом. Вот почему многие системы работают с центами (как целые числа) вместо долларов / евро (как с плавающей запятой).
Не элегантно, но делает работу (удаляет завершающие нули)
var num = 0.1*0.2;
alert(parseFloat(num.toFixed(10))); // shows 0.02
Элегантный, предсказуемый и многоразовый
Давайте разберемся с проблемой элегантным и многоразовым способом. Следующие семь строк позволят вам получить желаемую точность с плавающей запятой для любого числа, просто добавив.decimal до конца числа, формулы или встроенного Math функция.
// First extend the native Number object to handle precision. This populates
// the functionality to all math operations.
Object.defineProperty(Number.prototype, "decimal", {
get: function decimal() {
Number.precision = "precision" in Number ? Number.precision : 3;
var f = Math.pow(10, Number.precision);
return Math.round( this * f ) / f;
}
});
// Now lets see how it works by adjusting our global precision level and
// checking our results.
console.log("'1/3 + 1/3 + 1/3 = 1' Right?");
console.log((0.3333 + 0.3333 + 0.3333).decimal == 1); // true
console.log(0.3333.decimal); // 0.333 - A raw 4 digit decimal, trimmed to 3...
Number.precision = 3;
console.log("Precision: 3");
console.log((0.8 + 0.2).decimal); // 1
console.log((0.08 + 0.02).decimal); // 0.1
console.log((0.008 + 0.002).decimal); // 0.01
console.log((0.0008 + 0.0002).decimal); // 0.001
Number.precision = 2;
console.log("Precision: 2");
console.log((0.8 + 0.2).decimal); // 1
console.log((0.08 + 0.02).decimal); // 0.1
console.log((0.008 + 0.002).decimal); // 0.01
console.log((0.0008 + 0.0002).decimal); // 0
Number.precision = 1;
console.log("Precision: 1");
console.log((0.8 + 0.2).decimal); // 1
console.log((0.08 + 0.02).decimal); // 0.1
console.log((0.008 + 0.002).decimal); // 0
console.log((0.0008 + 0.0002).decimal); // 0
Number.precision = 0;
console.log("Precision: 0");
console.log((0.8 + 0.2).decimal); // 1
console.log((0.08 + 0.02).decimal); // 0
console.log((0.008 + 0.002).decimal); // 0
console.log((0.0008 + 0.0002).decimal); // 0Ура!
проблема
Плавающая точка не может хранить все десятичные значения точно. Поэтому при использовании форматов с плавающей запятой всегда будут ошибки округления входных значений. Ошибки на входах курса приводят к ошибкам на выходе. В случае дискретной функции или оператора на выходе могут быть большие различия вокруг точки, где функция или оператор дискретны.
Ввод и вывод для значений с плавающей запятой
Таким образом, при использовании переменных с плавающей запятой вы всегда должны знать об этом. И любой вывод, который вы хотите получить из вычисления с плавающей запятой, всегда должен быть отформатирован / подготовлен перед отображением с учетом этого.
Когда используются только непрерывные функции и операторы, часто выполняется округление до желаемой точности (не усекайте). Стандартные функции форматирования, используемые для преобразования чисел с плавающей точкой, обычно делают это для вас.
Поскольку при округлении добавляется ошибка, которая может привести к тому, что общая ошибка составляет более половины требуемой точности, выходные данные следует корректировать на основе ожидаемой точности входных данных и требуемой точности выходных данных. Вам следует
- Округлите ввод с ожидаемой точностью или убедитесь, что никакие значения не могут быть введены с большей точностью.
- Перед округлением / форматированием добавьте к выходным значениям небольшое значение, которое меньше или равно 1/4 требуемой точности и больше максимальной ожидаемой ошибки, вызванной ошибками округления на входе и во время расчета. Если это невозможно, комбинации точности используемого типа данных недостаточно, чтобы обеспечить желаемую точность вывода для ваших расчетов.
Эти две вещи, как правило, не выполняются, и в большинстве случаев различия, вызванные их отсутствием, слишком малы, чтобы быть важными для большинства пользователей, но у меня уже был проект, в котором вывод не был принят пользователями без этих исправлений.
Дискретные функции или операторы (например, по модулю)
Когда задействованы дискретные операторы или функции, могут потребоваться дополнительные корректировки, чтобы убедиться, что выходные данные соответствуют ожидаемым. Округление и добавление небольших исправлений перед округлением не может решить проблему.
Может потребоваться специальная проверка / исправление промежуточных результатов расчета сразу после применения дискретной функции или оператора. Для конкретного случая (оператор по модулю), см. Мой ответ на вопрос: Почему оператор модуля возвращает дробное число в JavaScript?
Лучше избегать проблем
Часто более эффективно избегать этих проблем, используя типы данных (целочисленные или фиксированные форматы) для таких вычислений, которые могут хранить ожидаемый ввод без ошибок округления. Примером этого является то, что вы никогда не должны использовать значения с плавающей запятой для финансовых расчетов.
С моей точки зрения, идея здесь состоит в том, чтобы округлить число fp, чтобы получить красивое / короткое строковое представление по умолчанию.
53-битная точность значащей дает от 15 до 17 значащих десятичных цифр (2-53 ≈ 1,11 × 10-16). Если десятичная строка, содержащая не более 15 значащих цифр, преобразована в представление двойной точности IEEE 754, а затем преобразована обратно в десятичную строку с тем же количеством цифр, окончательный результат должен соответствовать исходной строке. Если число двойной точности IEEE 754 преобразовано в десятичную строку, содержащую не менее 17 значащих цифр, а затем преобразовано обратно в представление двойной точности, окончательный результат должен соответствовать исходному числу.
...
С 52 битами значимой дроби (F), появляющимися в формате памяти, общая точность составляет 53 бита (приблизительно 16 десятичных цифр, 53 log10(2) ≈ 15,955). Биты расположены следующим образом... википедия
(0.1).toPrecision(100) ->
0.1000000000000000055511151231257827021181583404541015625000000000000000000000000000000000000000000000
(0.1+0.2).toPrecision(100) ->
0.3000000000000000444089209850062616169452667236328125000000000000000000000000000000000000000000000000
Затем, насколько я понимаю, мы можем округлить значение до 15 цифр, чтобы сохранить красивое строковое представление.
10**Math.floor(53 * Math.log10(2)) // 1e15
например.
Math.round((0.2+0.1) * 1e15 ) / 1e15
0.3
(Math.round((0.2+0.1) * 1e15 ) / 1e15).toPrecision(100)
0.2999999999999999888977697537484345957636833190917968750000000000000000000000000000000000000000000000
Функция будет такой:
function roundNumberToHaveANiceDefaultStringRepresentation(num) {
const integerDigits = Math.floor(Math.log10(Math.abs(num))+1);
const mult = 10**(15-integerDigits); // also consider integer digits
return Math.round(num * mult) / mult;
}
Вы не можете представлять большинство десятичных дробей точно с двоичными типами с плавающей запятой (это то, что ECMAScript использует для представления значений с плавающей запятой). Таким образом, не существует элегантного решения, если вы не используете арифметические типы произвольной точности или тип с плавающей запятой в десятичной форме. Например, приложение Calculator, поставляемое с Windows, теперь использует произвольную арифметику точности для решения этой проблемы.
Взгляните на арифметику с фиксированной точкой. Вероятно, это решит вашу проблему, если диапазон чисел, с которыми вы хотите работать, невелик (например, валюта). Я бы округлил его до нескольких десятичных значений, что является самым простым решением.
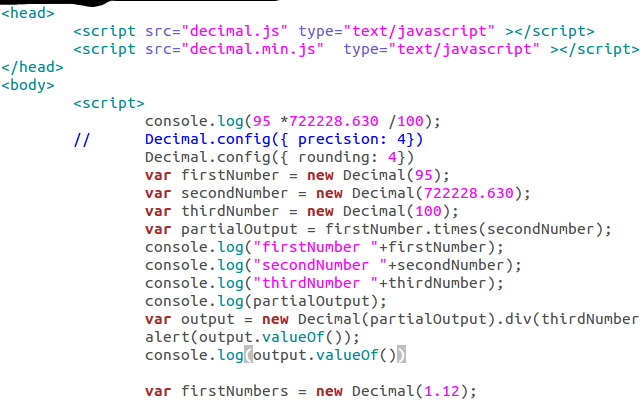
You can use library https://github.com/MikeMcl/decimal.js/.
it will help lot to give proper solution.
javascript console output 95 *722228.630 /100 = 686117.1984999999
decimal library implementation
var firstNumber = new Decimal(95);
var secondNumber = new Decimal(722228.630);
var thirdNumber = new Decimal(100);
var partialOutput = firstNumber.times(secondNumber);
console.log(partialOutput);
var output = new Decimal(partialOutput).div(thirdNumber);
alert(output.valueOf());
console.log(output.valueOf())== 686117.1985
Попробуйте мою chiliadic арифметическую библиотеку, которую вы можете увидеть здесь. Если вы хотите более позднюю версию, я могу получить ее.
Я не мог найти решение, используя встроенный
Number.EPSILON это призвано помочь с такого рода проблемами, поэтому вот мое решение:
function round(value, precision) {
const power = Math.pow(10, precision)
return Math.round((value*power)+(Number.EPSILON*power)) / power
}
При этом используется известная наименьшая разница между 1 и наименьшим числом с плавающей запятой больше единицы, чтобы исправить ошибку округления, заканчивающуюся всего одним
EPSILON ниже порога округления.
Максимальная точность
15 for 64bit с плавающей точкой и
6 for 32bitплавающая запятая. Ваш javascript, скорее всего, 64-битный.
Избегайте работы с плавающей запятой во время операции с целыми числами
Как указано в ответе, получившем наибольшее количество голосов до сих пор, вы можете работать с целыми числами, что означало бы умножить все ваши множители на 10 для каждого десятичного числа, с которым вы работаете, и разделить результат на то же используемое число.
Например, если вы работаете с двумя десятичными знаками, вы умножаете все свои множители на 100 перед выполнением операции, а затем делите результат на 100.
Вот пример, Result1 - обычный результат, Result2 - решение:
var Factor1="1110.7";
var Factor2="2220.2";
var Result1=Number(Factor1)+Number(Factor2);
var Result2=((Number(Factor1)*100)+(Number(Factor2)*100))/100;
var Result3=(Number(parseFloat(Number(Factor1))+parseFloat(Number(Factor2))).toPrecision(2));
document.write("Result1: "+Result1+"<br>Result2: "+Result2+"<br>Result3: "+Result3);Третий результат - показать, что происходит при использовании вместо него parseFloat, что в нашем случае привело к конфликту.
Отсутствие точности в программировании для значений с плавающей запятой
Отсутствие точности в программировании для значений с плавающей запятой — известная проблема в разных языках программирования. Javascript — один из тех, у которых есть проблемы с математикой со значениями с плавающей запятой. Такая проблема в основном связана с двоичным представлением чисел с плавающей запятой в памяти, выполняемым этими языками программирования.
Будем надеяться, что языки программирования и компиляторы, разработчики и инженеры аппаратного обеспечения займутся такими вопросами, решив их раз и навсегда хотя бы до числа с плавающей запятой 1024... вероятно, этого будет достаточно, чтобы 99,999% всех другие разработчики для следующего века программирования...
Возможное решение: преобразовать в целое число, вычислить, а затем обратно
Возможным решением может быть просто преобразование чисел с плавающей запятой в целые числа, выполнение вычислений и затем преобразование результата обратно в число с плавающей запятой. Кажется, это работает, большую часть времени. В принципе:
Вы правы, причина этого - ограниченная точность чисел с плавающей запятой. Храните ваши рациональные числа как деление двух целых чисел, и в большинстве случаев вы сможете хранить числа без потери точности. Когда дело доходит до печати, вы можете отобразить результат в виде дроби. С представлением я предложил, это становится тривиальным.
Конечно, это не очень поможет с иррациональными числами. Но вы можете оптимизировать свои вычисления таким образом, чтобы они вызывали наименьшую проблему (например, обнаружение таких ситуаций, как sqrt(3)^2),