Найдите самую большую выпуклую черную область на изображении

Question

У меня есть изображение, это небольшой вырез:

Как видите, это белые пиксели на черном фоне. Мы можем нарисовать воображаемые линии между этими пикселями (или, точнее, точками). С этими линиями мы можем заключить области.

Как я могу найти самую большую выпуклую черную область на этом изображении, в которой нет белого пикселя?

Вот небольшой нарисованный от руки пример того, что я подразумеваю под самой большой выпуклой черной областью:

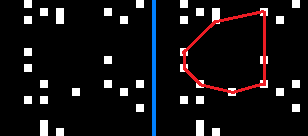
PS: изображение не является шумом, оно представляет простые числа ниже 10000000, упорядоченные по горизонтали.

Answer 1

Я нарисую правильный, многополосный алгоритм. Несомненно, необходимо внести структурные улучшения данных, но я полагаю, что, в частности, потребуется лучшее понимание этой проблемы для поиска очень больших наборов данных (или, возможно, специальной верхней границы для размеров блока, содержащего многоугольник).

Основной цикл состоит в угадывании самой низкой точки p в самом большом выпуклом многоугольнике (разрыв связи в пользу самой левой точки) и затем вычислении самого большого выпуклого многоугольника, который может быть с p и точками q, такими, что (qy > py) || (qy == py && qx > px).

Динамическая программа опирается на те же геометрические факты, что и сканирование Грэма. Предположим без ограничения общности, что p = (0, 0), и отсортируем точки q по углу, который они делают против часовой стрелки с осью x (сравните две точки, рассматривая знак их точечного произведения). Пусть точки в отсортированном порядке имеют вид q₁,…, q_n. Пусть q₀ = p. Для каждого 0 ≤ i 0, подмножестве q₁,…, q_{i - 1}, q_i и q_j.

Базовые случаи, когда i = 0, являются простыми, поскольку единственным "многоугольником" является сегмент нулевой области q₀ q_j. Индуктивно, чтобы вычислить запись (i, j), мы попробуем для всех 0 ≤ k ≤ i расширить полигон (k, i) с помощью (i, j). Когда мы сможем это сделать? Во-первых, треугольник q₀ q_i q_j не должен содержать других точек. Другое условие заключается в том, что угол q_k q_i q_j лучше не поворачивать направо (еще раз проверьте знак соответствующего точечного произведения).

В конце верните самый большой найденный многоугольник. Почему это работает? Нетрудно доказать, что выпуклые многоугольники имеют оптимальную подструктуру, требуемую динамической программой, и что программа рассматривает именно те многоугольники, которые удовлетворяют характеристике выпуклости Грэма.

Answer 2

Попытка найти максимальную выпуклую область - трудная задача. Разве вы не будете в порядке с поиском прямоугольников с максимальной площадью? Эта проблема намного проще и может быть решена за O(n) - линейное время в количестве пикселей. Алгоритм следующий.

Скажем, вы хотите найти самый большой прямоугольник из свободных (белых) пикселей (извините, у меня есть изображения с разными цветами - белый эквивалент вашего черного, серый - вашего белого).

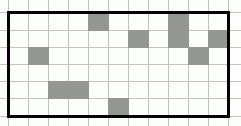
Вы можете сделать это очень эффективно с помощью двухпроходного линейного O(n) алгоритм времени (n - количество пикселей):

1) в первом проходе перейдите по столбцам снизу вверх и для каждого пикселя обозначьте число последовательных пикселей, доступных до этого:

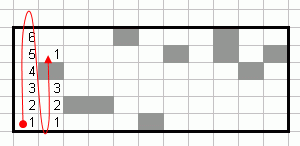
повторять, пока:

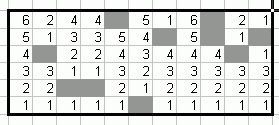
2) во второй проход, пройтись по строкам, прочитать current_number, Для каждого номера k отслеживать суммы последовательных номеров, которые были >= k (т.е. потенциальные прямоугольники высоты k). Закройте суммы (потенциальные прямоугольники) для k > current_number и посмотрите, больше ли сумма (~ площадь прямоугольника), чем текущий максимум - если да, обновите максимум. В конце каждой строки закройте все открытые потенциальные прямоугольники (для всех k).

Таким образом, вы получите все максимальные прямоугольники. Конечно, это не то же самое, что максимальная выпуклая область, но, вероятно, даст вам некоторые подсказки (некоторые эвристики) о том, где искать максимальные выпуклые области.

Answer 3

Вы можете попробовать обработать пиксели как вершины и выполнить триангуляцию Делоне для набора точек. Тогда вам нужно будет найти самый большой набор соединенных треугольников, который не создает вогнутую форму и не имеет внутренних вершин.

Answer 4

Если я правильно понимаю вашу проблему, это пример маркировки подключенных компонентов. Вы можете начать, например, с: http://en.wikipedia.org/wiki/Connected-component_labeling

Answer 5

Я подумал о подходе к решению этой проблемы:

Из множества всех точек генерируют все возможные 3-точечные подмножества. Это набор всех треугольников в вашем пространстве. Из этого набора удалите все треугольники, которые содержат другую точку, и вы получите набор всех пустых треугольников.

Для каждого из пустых треугольников вы бы увеличили его до максимального размера. То есть для каждой точки за пределами прямоугольника вы должны вставить ее между двумя ближайшими точками многоугольника и проверить, есть ли точки в этом новом треугольнике. Если нет, вы запомните эту точку и область, которую она добавляет. Для каждой новой точки вы хотите добавить ту, которая максимизирует добавленную область. Когда больше точки не могут быть добавлены, был построен максимальный выпуклый многоугольник. Запишите область для каждого многоугольника и запомните область с наибольшей площадью.

Решающее значение для эффективности этого алгоритма имеет ваша способность определить, а) находится ли точка внутри треугольника и б) остается ли многоугольник выпуклым после добавления определенной точки.

Я думаю, что вы можете уменьшить б), чтобы быть проблемой а), и тогда вам нужно только найти наиболее эффективный метод, чтобы определить, находится ли точка в треугольнике. Сокращение пространства поиска может быть достигнуто следующим образом: возьмите треугольник и увеличьте все ребра до бесконечной длины в обоих направлениях. Это разделяет область за пределами треугольника на 6 субрегионов. Хорошо для нас, что только 3 из этих субрегионов могут содержать точки, которые будут придерживаться ограничения выпуклости. Таким образом, для каждой проверяемой точки вам нужно определить, находится ли она в выпукло-расширяющемся субрегионе, что опять же является вопросом о том, находится ли она в определенном треугольнике.

Весь многоугольник, когда он развивается и приближается к форме круга, будет иметь меньшие и меньшие области, которые все еще допускают выпуклое расширение. Однажды точка в вогнутой области больше не станет частью выпукло-расширяющейся области, поэтому вы можете быстро уменьшить количество точек, которые вам нужно учитывать для расширения. Кроме того, при тестировании точек на расширение вы можете дополнительно сократить список возможных точек. Если точка проверена как ложная, то она находится в вогнутом субрегионе другой точки, и, следовательно, все другие точки в вогнутом субрегионе проверенных точек не должны рассматриваться, поскольку они также находятся в вогнутом субрегионе внутренней точки. Вы должны быть в состоянии сократить список возможных точек очень быстро.

Тем не менее, вы должны сделать это для каждого пустого треугольника, конечно.

К сожалению, я не могу гарантировать, что при добавлении максимально нового региона ваш полигон становится максимально возможным полигоном.