Расчет внутреннего продукта L2 в NumPy?

Question

Я думаю о внутреннем продукте L2.

Я особенно заинтересован в выполнении этих расчетов, используя numpy/scipy. Лучшее, что я придумал, - это выполнение интеграла на основе массива, такого как numpy.trapz,

import numpy as np
n=100000.
h=1./n
X = np.linspace(-np.pi,np.pi,n)

def L2_inner_product(f,g):
    return np.trapz(f*g,dx=2*np.pi*h)/np.pi

print L2_inner_product(np.sin(X), np.sin(X))
print L2_inner_product(np.cos(2*X), np.cos(2*X))
print L2_inner_product(np.sin(X), np.cos(X))
print L2_inner_product(np.sin(X), np.cos(3*X))
print L2_inner_product(np.ones(n),np.ones(n))

0.99999
0.99999
-3.86525742539e-18
1.6565388966e-18
1.99998

Чтобы было ясно, я не заинтересован в использовании Mathematica, Sage или Sympy. Я особенно заинтересован в numpy/scipy, в котором я исследую numpy "пространство массивов" как конечное подпространство Гильбертова пространства. В рамках этих параметров другие разработали внутренний продукт L2, возможно, используя numpy.inner или же numpy.linalg.norm?

Answer 1

Что касается скорости, numpy.inner вероятно, лучший выбор для фиксированной n, numpy.trapz должно сходиться быстрее, хотя. В любом случае, если вас беспокоит скорость, вы должны также принять во внимание, что оценка самих функций также займет некоторое время.

Ниже некоторого простого теста я использовал разные внутренние реализации продукта.

Задержки

На графике ниже показано время выполнения для вычисления только интеграла, т.е. не оценки функции. В то время как numpy.trapz постоянный фактор медленнее, numpy.inner так же быстро, как непосредственно звонить BLAS. Как указал Офион, numpy.inner вызывает BLAS внутренне, возможно, с некоторыми накладными расходами для проверки ввода.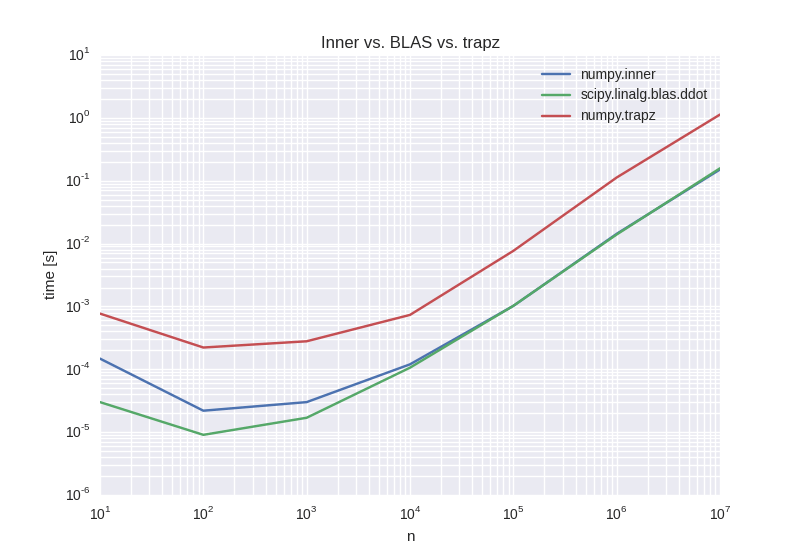

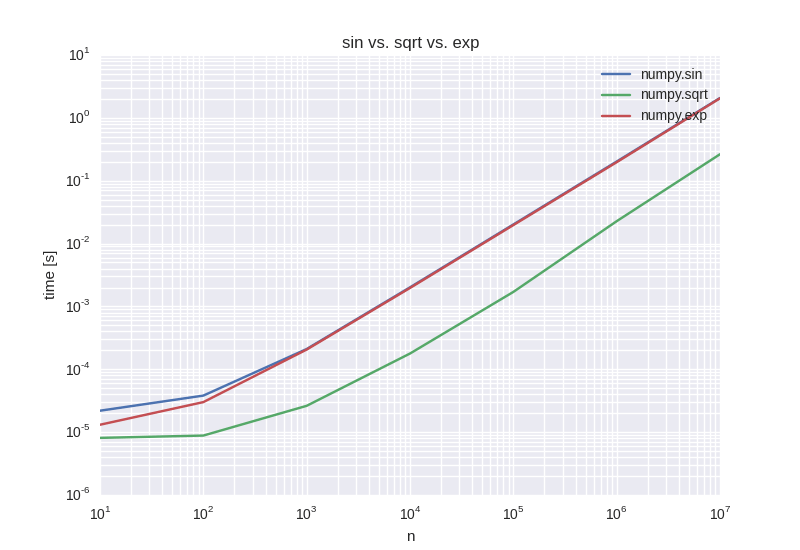
Также интересно взглянуть на время, необходимое для оценки самой функции, что, конечно же, необходимо для вычисления внутреннего продукта. Ниже графика, который показывает оценку для стандартных трансцендентных функций numpy.sin, numpy.sqrt а также numpy.exp, Масштабирование, конечно, одинаково для оценки и суммирования продуктов, и общее требуемое время сопоставимо

ошибка

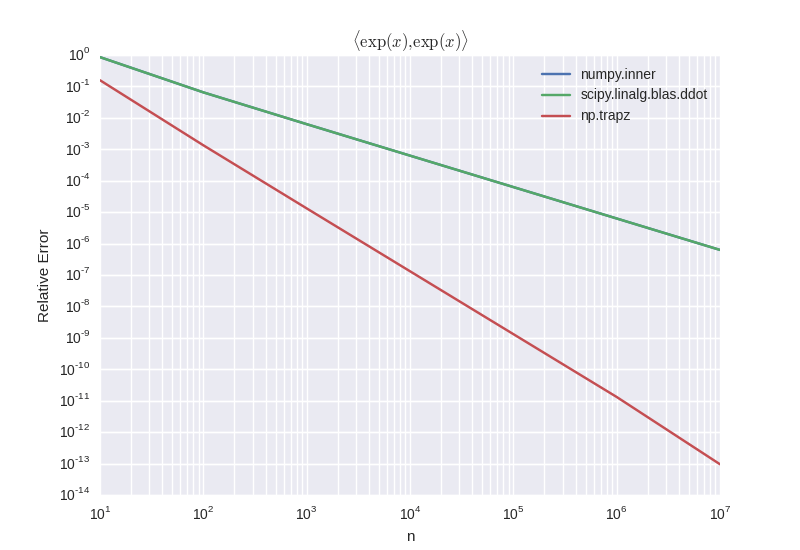
Наконец, следует также учитывать точность различных методов, и именно здесь это становится действительно интересным. Ниже приведен график сходимости различных реализаций для расчета , Здесь мы можем видеть, что numpy.trapz на самом деле масштабируется намного лучше, чем две другие реализации, которые даже не достигают точности машины, пока у меня не кончится память.

Заключение

Учитывая плохие свойства сходимости numpy.innerЯ бы пошел на numpy.trapz, Но даже тогда требуется много узлов интеграции, чтобы получить удовлетворительную точность. Поскольку ваш домен интеграции фиксирован, вы можете даже попробовать использовать квадратуры более высокого порядка.

Код

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sls
from scipy.linalg.blas import ddot
import timeit

## Define inner product.
def l2_inner_blas( f, g, dx ):
    return ddot( f, g )*dx / np.pi

def l2_inner( f, g, dx ):
    return np.inner( f, g )*dx / np.pi

def l2_inner_trapz( f, g, dx ):
    return np.trapz(f*g,dx=dx) / np.pi

sin1 = lambda x: np.sin( x )
sin2 = lambda x: np.sin( 2.0 * x)

## Timing setups.
setup1 = "import numpy as np; from __main__ import l2_inner,"
setup1 += "l2_inner_trapz, l2_inner_blas, sin1, sin2;"
setup1 += "n=%d; x=np.linspace(-np.pi,np.pi,n); dx=2.0*np.pi/(n-1);"
setup1 += "f=sin1(x); g=sin2(x);"

def time( n ):
    setupstr = setup1 % n
    time1 = timeit.timeit( 'l2_inner( f, g, dx)', setupstr, number=10 )
    time2 = timeit.timeit( 'l2_inner_blas( f, g, dx)', setupstr, number=10 )
    time3 = timeit.timeit( 'l2_inner_trapz( f, g, dx)', setupstr, number=10 )
    return (time1, time2, time3)

setup2 = "import numpy as np; x = np.linspace(-np.pi,np.pi,%d);"
def time_eval( n ):
    setupstr = setup2 % n
    time_sin = timeit.timeit( 'np.sin(x)', setupstr, number=10 )
    time_sqrt = timeit.timeit( 'np.sqrt(x)', setupstr, number=10 )
    time_exp = timeit.timeit( 'np.exp(x)', setupstr, number=10 )
    return (time_sin, time_sqrt, time_exp)

## Perform timing for vector product.
times = np.zeros( (7,3) )
for i in range(7):
    times[i,:] = time( 10**(i+1) )

x = 10**np.arange(1,8,1)
f, ax = plt.subplots()
ax.set( xscale='log', yscale='log', title='Inner vs. BLAS vs. trapz', \
        ylabel='time [s]', xlabel='n')
ax.plot( x, times[:,0], label='numpy.inner' )
ax.plot( x, times[:,1], label='scipy.linalg.blas.ddot')
ax.plot( x, times[:,2], label='numpy.trapz')
plt.legend()

## Perform timing for function evaluation.
times_eval = np.zeros( (7,3) )
for i in range(7):
    times_eval[i,:] = time_eval( 10**(i+1) )

x = 10**np.arange(1,8,1)
f, ax = plt.subplots()
ax.set( xscale='log', yscale='log', title='sin vs. sqrt vs. exp', \
        ylabel='time [s]', xlabel='n')
ax.plot( x, times_eval[:,0], label='numpy.sin' )
ax.plot( x, times_eval[:,1], label='numpy.sqrt')
ax.plot( x, times_eval[:,2], label='numpy.exp' )
plt.legend()

## Test convergence.
def error( n ):
    x = np.linspace( -np.pi, np.pi, n )
    dx = 2.0 * np.pi / (n-1)
    f = np.exp( x )
    l2 = 0.5/np.pi*(np.exp(2.0*np.pi) - np.exp(-2.0*np.pi))
    err1 = np.abs( (l2 - l2_inner( f, f, dx )) / l2)
    err2 = np.abs( (l2 - l2_inner_blas( f, f, dx )) / l2)
    err3 = np.abs( (l2 - l2_inner_trapz( f, f, dx )) / l2)
    return (err1, err2, err3)

acc = np.zeros( (7,3) )
for i in range(7):
    acc[i,:] = error( 10**(i+1) )

x = 10**np.arange(1,8,1)
f, ax = plt.subplots()
ax.plot( x, acc[:,0], label='numpy.inner' )
ax.plot( x, acc[:,1], label='scipy.linalg.blas.ddot')
ax.plot( x, acc[:,2], label='numpy.trapz')
ax.set( xscale='log', yscale='log', title=r'$\langle \exp(x), \exp(x) \rangle$', \
        ylabel='Relative Error', xlabel='n')
plt.legend()