Самый эффективный способ найти наименьшее из 3 чисел Java?
У меня есть алгоритм, написанный на Java, который я хотел бы сделать более эффективным. Часть, которую, я думаю, можно сделать более эффективной, - это найти наименьшее из 3 чисел. В настоящее время я использую Math.min метод, как показано ниже:
double smallest = Math.min(a, Math.min(b, c));
Насколько это эффективно? Будет ли эффективнее заменить на операторы if, как показано ниже:
double smallest;
if (a <= b && a <= c) {
smallest = a;
} else if (b <= c && b <= a) {
smallest = b;
} else {
smallest = c;
}
Или если какой-либо другой способ более эффективен
Мне интересно, стоит ли менять то, что я сейчас использую?
Любое увеличение скорости было бы очень полезно
15 ответов
Нет, это серьезно не стоит менять. Подобные улучшения, которые вы получите, когда будете возиться с микрооптимизациями, не будут стоить того. Даже стоимость вызова метода будет удалена, если min Функция вызывается достаточно.
Если у вас есть проблемы с вашим алгоритмом, вам лучше всего рассмотреть макрооптимизацию ("общую картину", такую как выбор алгоритма или настройка) - в целом вы получите гораздо лучшие улучшения производительности.
И ваш комментарий, что удаление Math.pow дал улучшения могут быть правильными, но это потому, что это относительно дорогая операция. Math.min даже не будет близко к этому с точки зрения стоимости.
Для многих методов служебного типа библиотеки apache commons имеют надежные реализации, которые вы можете использовать или получить от них дополнительную информацию. В этом случае для org.apache.commons.lang.math.NumberUtils существует метод поиска наименьшего из трех двойных чисел. Их реализация практически идентична вашей первоначальной мысли:
public static double min(double a, double b, double c) {
return Math.min(Math.min(a, b), c);
}
double smallest = a;
if (smallest > b) smallest = b;
if (smallest > c) smallest = c;
Не обязательно быстрее, чем ваш код.
Позвольте мне сначала повторить то, что уже говорили другие, цитируя статью Дональда Кнута "Структурное программирование с переходом к утверждениям":
Мы должны забыть о малой эффективности, скажем, в 97% случаев: преждевременная оптимизация - корень всего зла.
Тем не менее, мы не должны упускать наши возможности в этих критических 3%. Хорошие программисты не будут погружены в самоуспокоенность из-за таких рассуждений, ему будет разумно внимательно посмотреть на критический код; но только после того, как этот код был идентифицирован.
(акцент мной)
Таким образом, если вы определили, что кажущаяся тривиальной операцией, такой как вычисление не менее трех чисел, является фактическим узким местом (то есть "критическими 3%") в вашем приложении, то вы можете рассмотреть возможность его оптимизации.
И в этом случае это действительно возможно: Math#min(double,double) Метод в Java имеет особую семантику:
Возвращает меньшее из двух двойных значений. То есть результатом является значение, близкое к отрицательной бесконечности. Если аргументы имеют одинаковое значение, результатом будет то же значение. Если любое из значений равно NaN, то результатом является NaN. В отличие от операторов численного сравнения, этот метод считает отрицательный ноль строго меньшим, чем положительный ноль. Если один аргумент положительный ноль, а другой отрицательный ноль, результат отрицательный ноль.
Можно взглянуть на реализацию и увидеть, что это на самом деле довольно сложно:
public static double min(double a, double b) {
if (a != a)
return a; // a is NaN
if ((a == 0.0d) &&
(b == 0.0d) &&
(Double.doubleToRawLongBits(b) == negativeZeroDoubleBits)) {
// Raw conversion ok since NaN can't map to -0.0.
return b;
}
return (a <= b) ? a : b;
}
Теперь может быть важно указать, что это поведение отличается от простого сравнения. Это легко проверить на следующем примере:
public class MinExample
{
public static void main(String[] args)
{
test(0.0, 1.0);
test(1.0, 0.0);
test(-0.0, 0.0);
test(Double.NaN, 1.0);
test(1.0, Double.NaN);
}
private static void test(double a, double b)
{
double minA = Math.min(a, b);
double minB = a < b ? a : b;
System.out.println("a: "+a);
System.out.println("b: "+b);
System.out.println("minA "+minA);
System.out.println("minB "+minB);
if (Double.doubleToRawLongBits(minA) !=
Double.doubleToRawLongBits(minB))
{
System.out.println(" -> Different results!");
}
System.out.println();
}
}
Однако: если лечение NaN положительный / отрицательный ноль не имеет отношения к вашему приложению, вы можете заменить решение, основанное на Math.min с решением, основанным на простом сравнении, и посмотреть, имеет ли это значение.
Это, конечно, будет зависеть от приложения. Вот простой, искусственный микробенчмарк (взятый с зерном соли!)
import java.util.Random;
public class MinPerformance
{
public static void main(String[] args)
{
bench();
}
private static void bench()
{
int runs = 1000;
for (int size=10000; size<=100000; size+=10000)
{
Random random = new Random(0);
double data[] = new double[size];
for (int i=0; i<size; i++)
{
data[i] = random.nextDouble();
}
benchA(data, runs);
benchB(data, runs);
}
}
private static void benchA(double data[], int runs)
{
long before = System.nanoTime();
double sum = 0;
for (int r=0; r<runs; r++)
{
for (int i=0; i<data.length-3; i++)
{
sum += minA(data[i], data[i+1], data[i+2]);
}
}
long after = System.nanoTime();
System.out.println("A: length "+data.length+", time "+(after-before)/1e6+", result "+sum);
}
private static void benchB(double data[], int runs)
{
long before = System.nanoTime();
double sum = 0;
for (int r=0; r<runs; r++)
{
for (int i=0; i<data.length-3; i++)
{
sum += minB(data[i], data[i+1], data[i+2]);
}
}
long after = System.nanoTime();
System.out.println("B: length "+data.length+", time "+(after-before)/1e6+", result "+sum);
}
private static double minA(double a, double b, double c)
{
return Math.min(a, Math.min(b, c));
}
private static double minB(double a, double b, double c)
{
if (a < b)
{
if (a < c)
{
return a;
}
return c;
}
if (b < c)
{
return b;
}
return c;
}
}
(Отказ от ответственности: микробенчмаркинг в Java - это искусство, и для получения более надежных результатов следует рассмотреть возможность использования JMH или Caliper).
Запуск этого с JRE 1.8.0_31 может привести к чему-то вроде
....
A: length 90000, time 545.929078, result 2.247805342620906E7
B: length 90000, time 441.999193, result 2.247805342620906E7
A: length 100000, time 608.046928, result 2.5032781001456387E7
B: length 100000, time 493.747898, result 2.5032781001456387E7
Это, по крайней мере, говорит о том, что здесь можно выжать несколько процентов (опять же, в очень искусственном примере).
Проанализировав это далее, взглянув на результаты разборки горячей точки, созданные с
java -server -XX:+UnlockDiagnosticVMOptions -XX:+TraceClassLoading -XX:+LogCompilation -XX:+PrintAssembly MinPerformance
можно увидеть оптимизированные версии обоих методов, minA а также minB,
Во-первых, вывод для метода, который использует Math.min:
Decoding compiled method 0x0000000002992310:
Code:
[Entry Point]
[Verified Entry Point]
[Constants]
# {method} {0x000000001c010910} 'minA' '(DDD)D' in 'MinPerformance'
# parm0: xmm0:xmm0 = double
# parm1: xmm1:xmm1 = double
# parm2: xmm2:xmm2 = double
# [sp+0x60] (sp of caller)
0x0000000002992480: mov %eax,-0x6000(%rsp)
0x0000000002992487: push %rbp
0x0000000002992488: sub $0x50,%rsp
0x000000000299248c: movabs $0x1c010cd0,%rsi
0x0000000002992496: mov 0x8(%rsi),%edi
0x0000000002992499: add $0x8,%edi
0x000000000299249c: mov %edi,0x8(%rsi)
0x000000000299249f: movabs $0x1c010908,%rsi ; {metadata({method} {0x000000001c010910} 'minA' '(DDD)D' in 'MinPerformance')}
0x00000000029924a9: and $0x3ff8,%edi
0x00000000029924af: cmp $0x0,%edi
0x00000000029924b2: je 0x00000000029924e8 ;*dload_0
; - MinPerformance::minA@0 (line 58)
0x00000000029924b8: vmovsd %xmm0,0x38(%rsp)
0x00000000029924be: vmovapd %xmm1,%xmm0
0x00000000029924c2: vmovapd %xmm2,%xmm1 ;*invokestatic min
; - MinPerformance::minA@4 (line 58)
0x00000000029924c6: nop
0x00000000029924c7: callq 0x00000000028c6360 ; OopMap{off=76}
;*invokestatic min
; - MinPerformance::minA@4 (line 58)
; {static_call}
0x00000000029924cc: vmovapd %xmm0,%xmm1 ;*invokestatic min
; - MinPerformance::minA@4 (line 58)
0x00000000029924d0: vmovsd 0x38(%rsp),%xmm0 ;*invokestatic min
; - MinPerformance::minA@7 (line 58)
0x00000000029924d6: nop
0x00000000029924d7: callq 0x00000000028c6360 ; OopMap{off=92}
;*invokestatic min
; - MinPerformance::minA@7 (line 58)
; {static_call}
0x00000000029924dc: add $0x50,%rsp
0x00000000029924e0: pop %rbp
0x00000000029924e1: test %eax,-0x27623e7(%rip) # 0x0000000000230100
; {poll_return}
0x00000000029924e7: retq
0x00000000029924e8: mov %rsi,0x8(%rsp)
0x00000000029924ed: movq $0xffffffffffffffff,(%rsp)
0x00000000029924f5: callq 0x000000000297e260 ; OopMap{off=122}
;*synchronization entry
; - MinPerformance::minA@-1 (line 58)
; {runtime_call}
0x00000000029924fa: jmp 0x00000000029924b8
0x00000000029924fc: nop
0x00000000029924fd: nop
0x00000000029924fe: mov 0x298(%r15),%rax
0x0000000002992505: movabs $0x0,%r10
0x000000000299250f: mov %r10,0x298(%r15)
0x0000000002992516: movabs $0x0,%r10
0x0000000002992520: mov %r10,0x2a0(%r15)
0x0000000002992527: add $0x50,%rsp
0x000000000299252b: pop %rbp
0x000000000299252c: jmpq 0x00000000028ec620 ; {runtime_call}
0x0000000002992531: hlt
0x0000000002992532: hlt
0x0000000002992533: hlt
0x0000000002992534: hlt
0x0000000002992535: hlt
0x0000000002992536: hlt
0x0000000002992537: hlt
0x0000000002992538: hlt
0x0000000002992539: hlt
0x000000000299253a: hlt
0x000000000299253b: hlt
0x000000000299253c: hlt
0x000000000299253d: hlt
0x000000000299253e: hlt
0x000000000299253f: hlt
[Stub Code]
0x0000000002992540: nop ; {no_reloc}
0x0000000002992541: nop
0x0000000002992542: nop
0x0000000002992543: nop
0x0000000002992544: nop
0x0000000002992545: movabs $0x0,%rbx ; {static_stub}
0x000000000299254f: jmpq 0x000000000299254f ; {runtime_call}
0x0000000002992554: nop
0x0000000002992555: movabs $0x0,%rbx ; {static_stub}
0x000000000299255f: jmpq 0x000000000299255f ; {runtime_call}
[Exception Handler]
0x0000000002992564: callq 0x000000000297b9e0 ; {runtime_call}
0x0000000002992569: mov %rsp,-0x28(%rsp)
0x000000000299256e: sub $0x80,%rsp
0x0000000002992575: mov %rax,0x78(%rsp)
0x000000000299257a: mov %rcx,0x70(%rsp)
0x000000000299257f: mov %rdx,0x68(%rsp)
0x0000000002992584: mov %rbx,0x60(%rsp)
0x0000000002992589: mov %rbp,0x50(%rsp)
0x000000000299258e: mov %rsi,0x48(%rsp)
0x0000000002992593: mov %rdi,0x40(%rsp)
0x0000000002992598: mov %r8,0x38(%rsp)
0x000000000299259d: mov %r9,0x30(%rsp)
0x00000000029925a2: mov %r10,0x28(%rsp)
0x00000000029925a7: mov %r11,0x20(%rsp)
0x00000000029925ac: mov %r12,0x18(%rsp)
0x00000000029925b1: mov %r13,0x10(%rsp)
0x00000000029925b6: mov %r14,0x8(%rsp)
0x00000000029925bb: mov %r15,(%rsp)
0x00000000029925bf: movabs $0x515db148,%rcx ; {external_word}
0x00000000029925c9: movabs $0x2992569,%rdx ; {internal_word}
0x00000000029925d3: mov %rsp,%r8
0x00000000029925d6: and $0xfffffffffffffff0,%rsp
0x00000000029925da: callq 0x00000000512a9020 ; {runtime_call}
0x00000000029925df: hlt
[Deopt Handler Code]
0x00000000029925e0: movabs $0x29925e0,%r10 ; {section_word}
0x00000000029925ea: push %r10
0x00000000029925ec: jmpq 0x00000000028c7340 ; {runtime_call}
0x00000000029925f1: hlt
0x00000000029925f2: hlt
0x00000000029925f3: hlt
0x00000000029925f4: hlt
0x00000000029925f5: hlt
0x00000000029925f6: hlt
0x00000000029925f7: hlt
Можно видеть, что обработка особых случаев требует определенных усилий - по сравнению с результатами, в которых используются простые сравнения, что довольно просто:
Decoding compiled method 0x0000000002998790:
Code:
[Entry Point]
[Verified Entry Point]
[Constants]
# {method} {0x000000001c0109c0} 'minB' '(DDD)D' in 'MinPerformance'
# parm0: xmm0:xmm0 = double
# parm1: xmm1:xmm1 = double
# parm2: xmm2:xmm2 = double
# [sp+0x20] (sp of caller)
0x00000000029988c0: sub $0x18,%rsp
0x00000000029988c7: mov %rbp,0x10(%rsp) ;*synchronization entry
; - MinPerformance::minB@-1 (line 63)
0x00000000029988cc: vucomisd %xmm0,%xmm1
0x00000000029988d0: ja 0x00000000029988ee ;*ifge
; - MinPerformance::minB@3 (line 63)
0x00000000029988d2: vucomisd %xmm1,%xmm2
0x00000000029988d6: ja 0x00000000029988de ;*ifge
; - MinPerformance::minB@22 (line 71)
0x00000000029988d8: vmovapd %xmm2,%xmm0
0x00000000029988dc: jmp 0x00000000029988e2
0x00000000029988de: vmovapd %xmm1,%xmm0 ;*synchronization entry
; - MinPerformance::minB@-1 (line 63)
0x00000000029988e2: add $0x10,%rsp
0x00000000029988e6: pop %rbp
0x00000000029988e7: test %eax,-0x27688ed(%rip) # 0x0000000000230000
; {poll_return}
0x00000000029988ed: retq
0x00000000029988ee: vucomisd %xmm0,%xmm2
0x00000000029988f2: ja 0x00000000029988e2 ;*ifge
; - MinPerformance::minB@10 (line 65)
0x00000000029988f4: vmovapd %xmm2,%xmm0
0x00000000029988f8: jmp 0x00000000029988e2
0x00000000029988fa: hlt
0x00000000029988fb: hlt
0x00000000029988fc: hlt
0x00000000029988fd: hlt
0x00000000029988fe: hlt
0x00000000029988ff: hlt
[Exception Handler]
[Stub Code]
0x0000000002998900: jmpq 0x00000000028ec920 ; {no_reloc}
[Deopt Handler Code]
0x0000000002998905: callq 0x000000000299890a
0x000000000299890a: subq $0x5,(%rsp)
0x000000000299890f: jmpq 0x00000000028c7340 ; {runtime_call}
0x0000000002998914: hlt
0x0000000002998915: hlt
0x0000000002998916: hlt
0x0000000002998917: hlt
Трудно сказать, есть ли случаи, когда такая оптимизация действительно имеет значение в приложении. Но, по крайней мере, суть заключается в следующем:
-
Math#min(double,double)метод не то же самое, что простое сравнение, и лечение особых случаев не приходит бесплатно - Есть случаи, когда особый случай лечения, который выполняется
Math#minне является необходимым, и тогда подход на основе сравнения может быть более эффективным - Как уже указывалось в других ответах: в большинстве случаев разница в производительности не имеет значения. Однако для этого конкретного примера, вероятно, следует создать служебный метод
min(double,double,double)во всяком случае, для лучшего удобства и удобочитаемости, а затем было бы легко выполнить два запуска с различными реализациями и посмотреть, действительно ли это влияет на производительность.
(Примечание: методы интегрального типа, такие как Math.min(int,int) на самом деле это простое сравнение - поэтому я не ожидал бы никакой разницы для них).
Вы можете использовать троичный оператор следующим образом:
smallest=(a<b)?((a<c)?a:c):((b<c)?b:c);
Который занимает только одно назначение и минимум два сравнения.
Но я думаю, что эти утверждения не повлияют на время выполнения, ваша первоначальная логика займет то же время, что и у меня, и у всех остальных.
В эффективном коде OP есть ошибка:
когда a == b, а также a (or b) < c, код выберет c вместо a или b.
Для тех, кто найдет эту тему намного позже:
Если у вас есть только три значения для сравнения, то нет существенной разницы. Но если вам нужно найти минимум из, скажем, тридцати или шестидесяти значений, "мин" будет проще для любого, кто будет читать код в следующем году:
int smallest;
smallest = min(a1, a2);
smallest = min(smallest, a3);
smallest = min(smallest, a4);
...
smallest = min(smallest, a37);
Но если вы думаете о скорости, возможно, лучшим способом было бы поместить значения в список, а затем найти минимум этого:
List<Integer> mySet = Arrays.asList(a1, a2, a3, ..., a37);
int smallest = Collections.min(mySet);
Вы бы согласились?
Math.min использует простое сравнение, чтобы сделать свое дело. Единственным преимуществом неиспользования Math.min является сохранение дополнительных вызовов функций, но это незначительное сохранение.
Если у вас есть более трех номеров, имея minimum метод для любого числа doubles может быть ценным и выглядеть примерно так:
public static double min(double ... numbers) {
double min = numbers[0];
for (int i=1 ; i<numbers.length ; i++) {
min = (min <= numbers[i]) ? min : numbers[i];
}
return min;
}
Для трех чисел это функциональный эквивалент Math.min(a, Math.min(b, c)); но вы сохраняете один вызов метода.
Используйте метод Arrays.sort(), наименьшее значение будет element0.
С точки зрения производительности это не должно быть дорогостоящим, поскольку операция сортировки уже оптимизирована. Также имеет преимущество краткости.
private int min(int ... value) {
Arrays.sort(value);
return value[0];
}
Доказательство концепции
int[] intArr = {12, 5, 6, 9, 44, 28, 1, 4, 18, 2, 66, 13, 1, 33, 74, 12,
5, 6, 9, 44, 28, 1, 4, 18, 2, 66, 13};
// Sorting approach
long startTime = System.currentTimeMillis();
int minVal = min(intArr);
long endTime = System.currentTimeMillis();
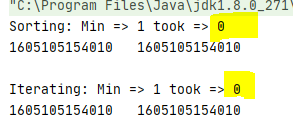
System.out.println("Sorting: Min => " + minVal + " took => " + (endTime -
startTime));
System.out.println(startTime + " " + endTime);
System.out.println(" ");
// Scanning approach
minVal = 100;
startTime = System.currentTimeMillis();
for(int val : intArr) {
if (val < minVal)
minVal = val;
}
endTime = System.currentTimeMillis();
System.out.println("Iterating: Min => " + minVal + " took => " + (endTime
- startTime));
System.out.println(startTime + " " + endTime);
Для чистой эффективности символов кода я не могу найти ничего лучше, чем
smallest = a<b&&a<c?a:b<c?b:c;
double smallest;
if(a<b && a<c){
smallest = a;
}else if(b<c && b<a){
smallest = b;
}else{
smallest = c;
}
можно улучшить до:
double smallest;
if(a<b && a<c){
smallest = a;
}else if(b<c){
smallest = b;
}else{
smallest = c;
}
Если вы будете вызывать min() около 1кк раз с разными a, b, c, то используйте мой метод:
Здесь только два сравнения. Нет возможности посчитать быстрее:P
public static double min(double a, double b, double c) {
if (a > b) { //if true, min = b
if (b > c) { //if true, min = c
return c;
} else { //else min = b
return b;
}
} //else min = a
if (a > c) { // if true, min=c
return c;
} else {
return a;
}
}
Все выглядит хорошо, ваш код будет в порядке, если вы не делаете это в тесном цикле. Я бы тоже посчитал
double min;
min = (a<b) ? a : b;
min = (min<c) ? min : c;
Я хотел бы использовать min/max (и не волнуйтесь иначе) ... однако, здесь есть другой подход "длинной руки", который может быть или не быть легче для некоторых людей, чтобы понять. (Я не ожидал бы, что это будет быстрее или медленнее, чем код в посте.)
int smallest;
if (a < b) {
if (a > c) {
smallest = c;
} else { // a <= c
smallest = a;
}
} else { // a >= b
if (b > c) {
smallest = c;
} else { // b <= c
smallest = b;
}
}
Просто бросаю это в смесь.
Обратите внимание, что это всего лишь побочный вариант ответа Абхишека.
Работает с произвольным количеством входных значений:
public static double min(double... doubles) {
double m = Double.MAX_VALUE;
for (double d : doubles) {
m = Math.min(m, d);
}
return m;
}
Напишите метод imum3, который возвращает наименьшее из трех чисел с плавающей точкой. Используйте метод Math.min для реализации минимума3. Включите метод в приложение, которое читает три значения от пользователя, определяет наименьшее значение и отображает результат.
Просто используйте эту математическую функцию
System.out.println(Math.min(a,b,c));
Вы получите ответ в одну строку.