Как я могу построить список, возвращаемый решением Mathematica в ограниченных целочисленных уравнениях

Question

Итак, у меня есть набор ограниченных диофантовых уравнений, которые задают линии на плоскости. Я хочу, чтобы математика построила пересечение двух из этих уравнений, чтобы я могла видеть, как они выглядят.

Пока что у меня есть что-то вроде:

Решить [0

который возвращает некоторую структуру, такую ​​как:

{{x -> -2, y -> -4}, {x -> -1, y -> -3}, {x -> -1, y -> -2}, {x -> 0, y -> -1}}

но как я могу теперь сделать Mathematica построить это так, чтобы я мог видеть полученную форму. Желательно, чтобы на графике каждая "точка" рассматривалась как квадрат 1х1.

Кроме того, мне интересно, есть ли лучший способ сделать такие вещи. Благодарю.

Answer 1

Определите данные, которые вы хотите построить, преобразовав список Solve[] возвращается. Это можно сделать как

 data = {x, y} /. Solve[0 < x - y < 3 && -1 < 2 x - y < 2, {x, y}, Integers]

В целом, вы можете сделать Solve вернуть решение в виде списка (а не в виде набора правил), используя следующий прием:

 data = Solve[0 < x - y < 3 && -1 < 2 x - y < 2, {x, y}, Integers] /. Rule[a_,b_]->b

Для построения графика, среди множества альтернатив, вы можете использовать ListPlot как

ListPlot[data, PlotMarkers -> {Style["\[FilledSquare]", FontSize -> 16]}]

чтобы получить следующий вывод

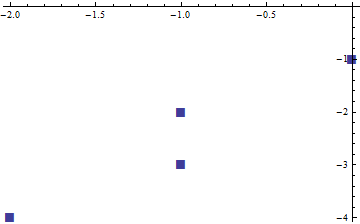
Вы можете уточнить его, используя множество стилей и других опций ListPlot, Например, вы можете присоединиться к точкам

ListPlot[data, PlotMarkers -> {Style["\[FilledSquare]", FontSize -> 16]}, 
 Joined -> True]

получить

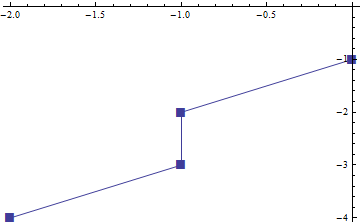
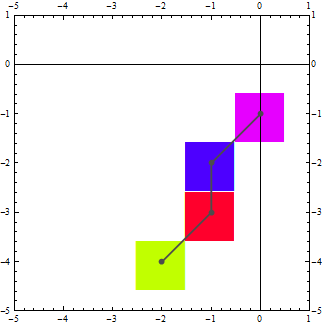
РЕДАКТИРОВАТЬ: Чтобы играть с размещением и размером маркера, есть несколько альтернатив. С помощью ListPlot Вы можете получить то, что вам нужно, одним из двух способов:

 (* Alternative 1: use fontsize to change the marker size *)
 lp1 := ListPlot[{#} & /@ #1, 
 PlotMarkers -> {Style["\[FilledSquare]", FontSize -> Scaled[#2]]},
 AspectRatio -> 1, AxesOrigin -> {0, 0}, 
 PlotRange -> {{-5, 1}, {-5, 1}}, 
 PlotStyle -> Hue /@ RandomReal[1, {Length@#1}], 
 Epilog -> {GrayLevel[.3], PointSize[.02], Point@#1, Thick, 
  Line@#1}, Frame -> True, FrameTicks -> All] &;
 (* usage example *)
 lp1 @@ {data, .30}

 (* Alternative 2: use the second parameter of PlotMarkers to control scaled size *)
 lp2 := ListPlot[{#} & /@ #1, 
 PlotMarkers -> {Graphics@{Rectangle[]}, #2}, AspectRatio -> 1, 
 AxesOrigin -> {0, 0}, PlotRange -> {{-5, 1}, {-5, 1}}, 
 PlotStyle -> Hue /@ RandomReal[1, {Length@#1}], 
 Epilog -> {GrayLevel[.3], PointSize[.02], Point@#1, Thick, 
 Line@#1}, Frame -> True, FrameTicks -> All] &
 (* usage example *)
 lp2 @@ {data, 1/5.75}

В обоих случаях вам нужно использовать Epilogв противном случае точки, соединяющие линии, закрываются маркерами. Обе альтернативы дают следующий результат:

Кроме того, вы можете использовать Graphics, RegionPlot, ContourPlot, BubbleChart с соответствующими преобразованиями data чтобы получить результаты, аналогичные тем, что в ListPlot выход выше.

Использование графических примитивов:

 (* data transformation to define the regions *)
 trdataG[data_, size_] :=  data /. {a_, b_} :> 
         {{a - size/2, b - size/2}, {a + size/2, b + size/2}};
 (* plotting function *)
 gr := Graphics[
      {
      {Hue[RandomReal[]], Rectangle[##]} & @@@ trdataG @@ {#1, #2}, 
      GrayLevel[.3], PointSize[.02], Thick, Point@#1, Line@#1}, 
      PlotRange -> {{-5, 1}, {-5, 1}
      }, 
      PlotRangePadding -> 0, Axes -> True, AxesOrigin -> {0, 0}, 
      Frame -> True, FrameTicks -> All] &
 (* usage example *)
 gr @@ {data, .99}

Используя BubbleChart:

 (* Transformation of data to a form that BubbleChart expects *)
 dataBC[data_] := data /. {a_, b_} :> {a, b, 1};
 (* custom markers *)
 myMarker[size_][{{xmin_, xmax_}, {ymin_, ymax_}}, ___] :=
      {EdgeForm[], Rectangle[{(1/2) (xmin + xmax) - size/2, (1/2) (ymin + ymax) - 
       size/2}, {(1/2) (xmin + xmax) + size/2, (1/2) (ymin + ymax) + size/2}]};
 (* charting function *)
 bc := BubbleChart[dataBC[#1], ChartElementFunction -> myMarker[#2], 
       ChartStyle -> Hue /@ RandomReal[1, {Length@#1}], Axes -> True, 
       AxesOrigin -> {0, 0}, PlotRange -> {{-5, 1}, {-5, 1}}, 
       PlotRangePadding -> 0, AspectRatio -> 1, FrameTicks -> All, 
       Epilog -> {GrayLevel[.3], PointSize[.02], Point@#1, Thick, Line@#1}] &
 (* usage example *)
 bc @@ {data, .99}

Использование RegionPlot:

 (* Transformation of data to a form that RegionPlot expects *)
  trdataRP[data_, size_] :=  data /. {a_, b_} :> 
            a - size/2 <= x <= a + size/2 && b - size/2 <= y <= b + size/2
 (* charting function *)
 rp := RegionPlot[Evaluate@trdataRP[#1, #2], {x, -5, 1}, {y, -5, 1}, 
          AspectRatio -> 1, Axes -> True, AxesOrigin -> {0, 0}, 
          PlotRange -> {{-5, 1}, {-5, 1}}, 
          PlotStyle -> Hue /@ RandomReal[1, {Length@#1}], FrameTicks -> All, 
          PlotPoints -> 100, BoundaryStyle -> None, 
          Epilog -> {GrayLevel[.3], PointSize[.02], Point@#1, Thick, Line@#1}] &
 (* usage example *)
 rp @@ {data, .99}

Использование ContourPlot:

 (* Transformation of data to a form that ContourPlot expects *)
 trdataRP[data_, size_] :=   data /. {a_, b_} :> 
            a - size/2 <= x <= a + size/2 && b - size/2 <= y <= b + size/2;
 trdataCP[data_, size_] := Which @@ Flatten@
           Thread[{trdataRP[data, size], Range@Length@data}];
 (* charting function *)
 cp := ContourPlot[trdataCP[#1, #2], {x, -5, 1}, {y, -5, 1}, 
             AspectRatio -> 1, Axes -> True, AxesOrigin -> {0, 0}, 
             PlotRange -> {{-5, 1}, {-5, 1}}, FrameTicks -> All, 
             ExclusionsStyle -> None, PlotPoints -> 100, 
             ColorFunction -> Hue, 
             Epilog -> {GrayLevel[.3], PointSize[.02], Point@#1, Thick, Line@#1}] &
 (* usage example *)
 cp @@ {data, .99}

Answer 2

Может быть

sol = Solve[0 < x - y < 3 && -1 < 2 x - y < 2, {x, y}, Integers];
pts = Cases[sol, {_ -> n_, _ -> m_} :> {n, m}];
ListPlot[pts, Mesh -> All, Joined -> True, AxesOrigin -> {0, 0}, 
 PlotMarkers -> {Automatic, 10}]

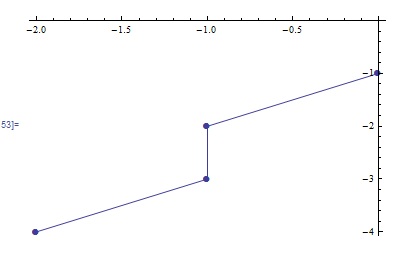
Можно также извлечь точки для построения графика, используя

{#[[1, 2]], #[[2, 2]]} & /@ sol