Промежуточный слой заставляет оптимизатор тензорного потока перестать работать
Этот график обучает простой кодер идентификатора сигнала и фактически показывает, что весовые коэффициенты определяются оптимизатором:
import tensorflow as tf
import numpy as np
initia = tf.random_normal_initializer(0, 1e-3)
DEPTH_1 = 16
OUT_DEPTH = 1
I = tf.placeholder(tf.float32, shape=[None,1], name='I') # input
W = tf.get_variable('W', shape=[1,DEPTH_1], initializer=initia, dtype=tf.float32, trainable=True) # weights
b = tf.get_variable('b', shape=[DEPTH_1], initializer=initia, dtype=tf.float32, trainable=True) # biases
O = tf.nn.relu(tf.matmul(I, W) + b, name='O') # activation / output
#W1 = tf.get_variable('W1', shape=[DEPTH_1,DEPTH_1], initializer=initia, dtype=tf.float32) # weights
#b1 = tf.get_variable('b1', shape=[DEPTH_1], initializer=initia, dtype=tf.float32) # biases
#O1 = tf.nn.relu(tf.matmul(O, W1) + b1, name='O1')
W2 = tf.get_variable('W2', shape=[DEPTH_1,OUT_DEPTH], initializer=initia, dtype=tf.float32) # weights
b2 = tf.get_variable('b2', shape=[OUT_DEPTH], initializer=initia, dtype=tf.float32) # biases
O2 = tf.matmul(O, W2) + b2
O2_0 = tf.gather_nd(O2, [[0,0]])
estimate0 = 2.0*O2_0
eval_inp = tf.gather_nd(I,[[0,0]])
k = 1e-5
L = 5.0
distance = tf.reduce_sum( tf.square( eval_inp - estimate0 ) )
opt = tf.train.GradientDescentOptimizer(1e-3)
grads_and_vars = opt.compute_gradients(distance, [W, b, #W1, b1,
W2, b2])
clipped_grads_and_vars = [(tf.clip_by_value(g, -4.5, 4.5), v) for g, v in grads_and_vars]
train_op = opt.apply_gradients(clipped_grads_and_vars)
saver = tf.train.Saver()
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init_op)
for i in range(10000):
print sess.run([train_op, I, W, distance], feed_dict={ I: 2.0*np.random.rand(1,1) - 1.0})
for i in range(10):
print sess.run([eval_inp, W, estimate0], feed_dict={ I: 2.0*np.random.rand(1,1) - 1.0})
Однако, когда я раскомментирую промежуточный скрытый слой и обучаю полученную сеть, я вижу, что веса больше не развиваются:
import tensorflow as tf
import numpy as np
initia = tf.random_normal_initializer(0, 1e-3)
DEPTH_1 = 16
OUT_DEPTH = 1
I = tf.placeholder(tf.float32, shape=[None,1], name='I') # input
W = tf.get_variable('W', shape=[1,DEPTH_1], initializer=initia, dtype=tf.float32, trainable=True) # weights
b = tf.get_variable('b', shape=[DEPTH_1], initializer=initia, dtype=tf.float32, trainable=True) # biases
O = tf.nn.relu(tf.matmul(I, W) + b, name='O') # activation / output
W1 = tf.get_variable('W1', shape=[DEPTH_1,DEPTH_1], initializer=initia, dtype=tf.float32) # weights
b1 = tf.get_variable('b1', shape=[DEPTH_1], initializer=initia, dtype=tf.float32) # biases
O1 = tf.nn.relu(tf.matmul(O, W1) + b1, name='O1')
W2 = tf.get_variable('W2', shape=[DEPTH_1,OUT_DEPTH], initializer=initia, dtype=tf.float32) # weights
b2 = tf.get_variable('b2', shape=[OUT_DEPTH], initializer=initia, dtype=tf.float32) # biases
O2 = tf.matmul(O1, W2) + b2
O2_0 = tf.gather_nd(O2, [[0,0]])
estimate0 = 2.0*O2_0
eval_inp = tf.gather_nd(I,[[0,0]])
distance = tf.reduce_sum( tf.square( eval_inp - estimate0 ) )
opt = tf.train.GradientDescentOptimizer(1e-3)
grads_and_vars = opt.compute_gradients(distance, [W, b, W1, b1,
W2, b2])
clipped_grads_and_vars = [(tf.clip_by_value(g, -4.5, 4.5), v) for g, v in grads_and_vars]
train_op = opt.apply_gradients(clipped_grads_and_vars)
saver = tf.train.Saver()
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init_op)
for i in range(10000):
print sess.run([train_op, I, W, distance], feed_dict={ I: 2.0*np.random.rand(1,1) - 1.0})
for i in range(10):
print sess.run([eval_inp, W, estimate0], feed_dict={ I: 2.0*np.random.rand(1,1) - 1.0})
Оценка estimate0 быстро сходится в некотором фиксированном значении, которое становится независимым от входного сигнала. Я понятия не имею, почему это происходит
Вопрос:
Есть идеи, что может быть не так со вторым примером?
1 ответ
TL;DR: чем глубже становится нейронная сеть, тем больше вы должны обращать внимание на поток градиента (см. Это обсуждение "исчезающих градиентов"). Один частный случай - инициализация переменных.
Анализ проблем
Я добавил резюме тензорной доски для переменных и градиентов в оба ваших скрипта и получил следующее:
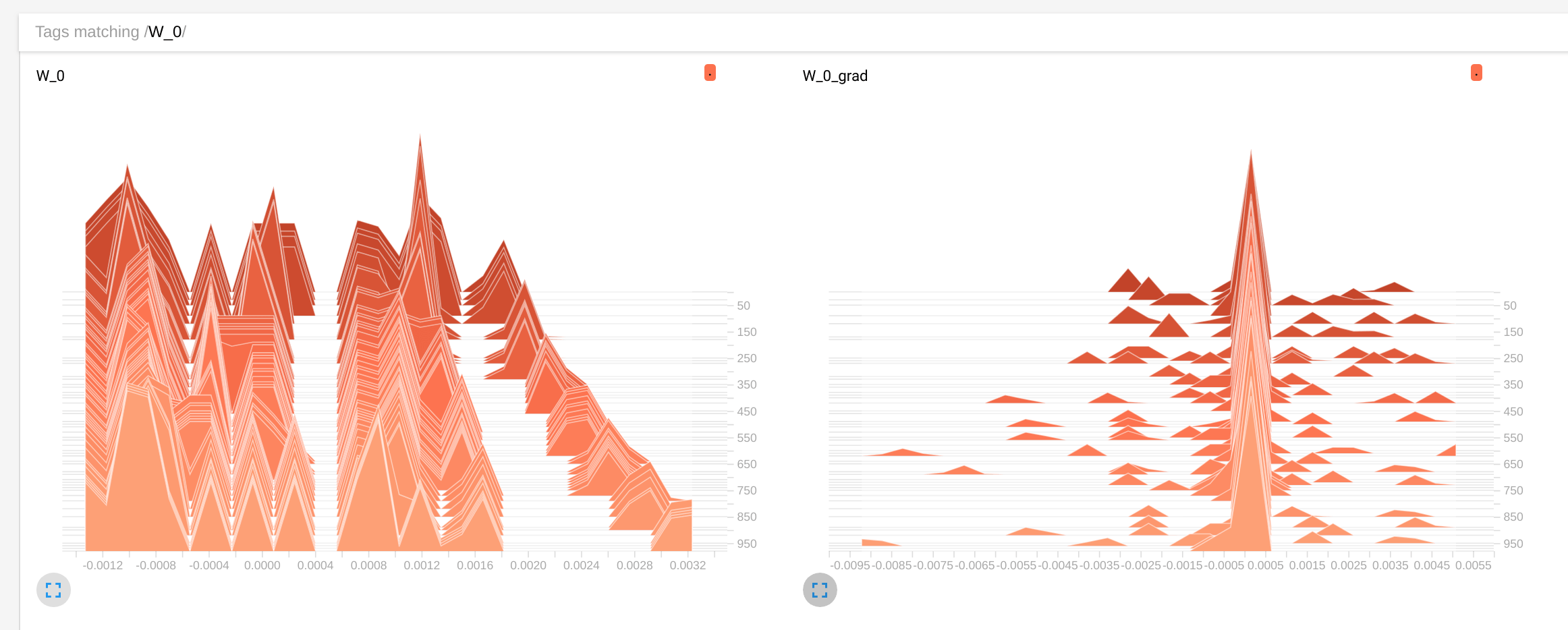
2-х слойная сеть
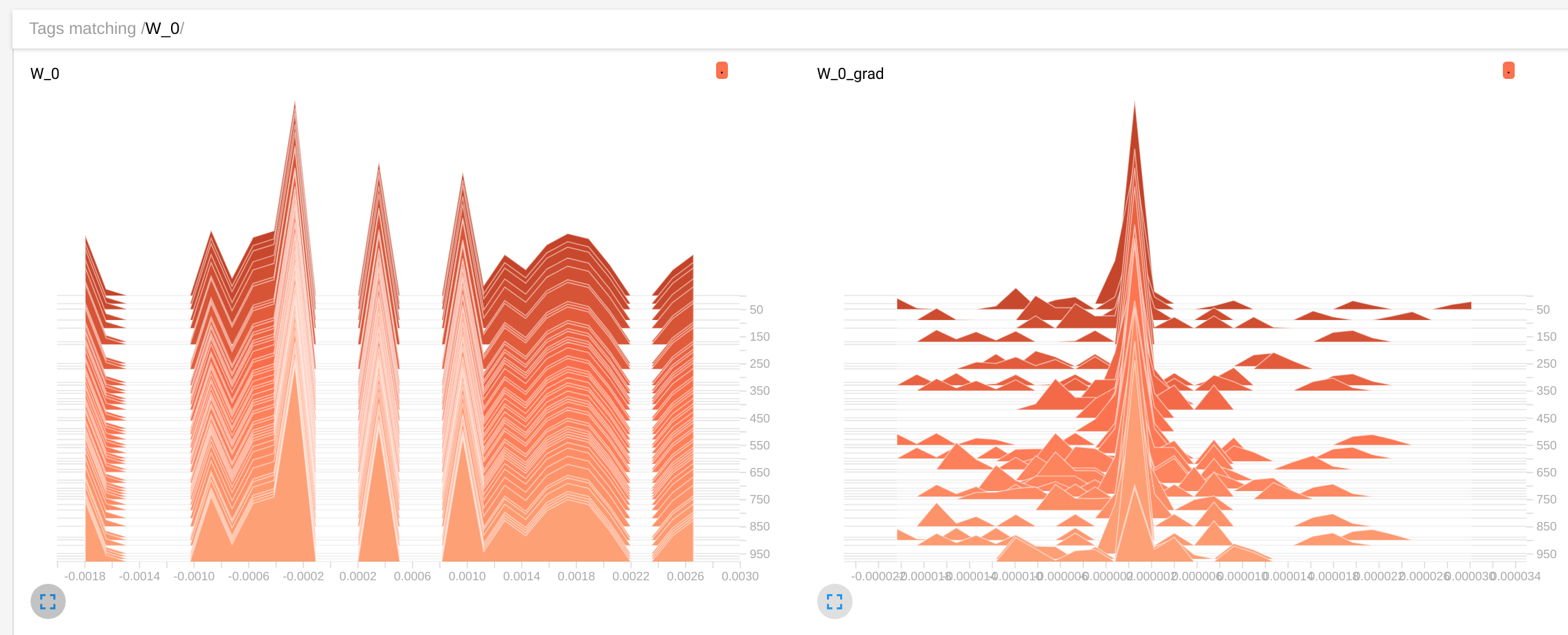
3-х слойная сеть
Графики показывают распределение W:0 переменная (первый слой) и как они изменяются с 0 эпох до 1000 (кликабельно). Действительно, мы можем видеть, что скорость изменения намного выше в двухслойной сети. Но я хотел бы обратить внимание на распределение градиента, которое намного ближе к 0 в 3-слойной сети (первая дисперсия около 0.005второй около 0.000002т.е. в 1000 раз меньше). Это исчезающая проблема градиента.
Вот вспомогательный код, если вам интересно:
for g, v in grads_and_vars:
tf.summary.histogram(v.name, v)
tf.summary.histogram(v.name + '_grad', g)
merged = tf.summary.merge_all()
writer = tf.summary.FileWriter('train_log_layer2', tf.get_default_graph())
...
_, summary = sess.run([train_op, merged], feed_dict={I: 2*np.random.rand(1, 1)-1})
if i % 10 == 0:
writer.add_summary(summary, global_step=i)
Решение
Все глубокие сети страдают от этого в некоторой степени, и не существует универсального решения, которое бы автоматически исправляло любую сеть. Но есть некоторые методы, которые могут подтолкнуть его в правильном направлении. Инициализация является одним из них.
Я заменил вашу обычную инициализацию на:
W_init = tf.contrib.layers.xavier_initializer()
b_init = tf.constant_initializer(0.1)
Существует множество учебных пособий по инициализации Xavier, вы можете взглянуть на это, например. Обратите внимание, что я установил, что init смещения слегка положительный, чтобы убедиться, что выходы ReLu положительны для большинства нейронов, по крайней мере, в начале.
Это сразу изменило картину:
Веса все еще движутся не так быстро, как раньше, но они движутся (обратите внимание на масштаб W:0 значения), и распределение градиентов стало намного менее пиковым в 0, таким образом намного лучше.
Конечно, это не конец. Чтобы еще больше улучшить его, вы должны реализовать полный автоэнкодер, потому что в настоящее время на потери влияет [0,0] восстановление элементов, поэтому большинство выходных данных не используются при оптимизации. Вы также можете играть с различными оптимизаторами (Адам был бы моим выбором) и темпами обучения.
Это выглядит очень захватывающе. Кому именно принадлежит этот код? Я только недавно открыл для себя TensorBoard
это как-то в обратных вызовах:
for g, v in grads_and_vars:
tf.summary.histogram(v.name, v)
tf.summary.histogram(v.name + '_grad', g)
merged = tf.summary.merge_all()
writer = tf.summary.FileWriter('train_log_layer2', tf.get_default_graph())
это после примерки:
_, summary = sess.run([train_op, merged], feed_dict={I: 2*np.random.rand(1, 1)-1})
if i % 10 == 0:
writer.add_summary(summary, global_step=i)