Неожиданный БПФ выходной импульсной характеристики интегратора - MATLAB

Question

Я пытаюсь получить частотный отклик любых передаточных функций, используя преобразование Фурье импульсного отклика системы. Это работает довольно хорошо для большинства протестированных случаев, но у меня все еще есть проблема с передаточными функциями, в которых есть интегратор (например, 1/s; (4s+2)/(3s^2+s) и т. Д.).

Давайте возьмем пример чистого интегратора с H(s) = 1/s. Полученный импульсный отклик, как и ожидалось, является ступенчатой ​​функцией, но преобразование Фурье импульсного отклика не дает ожидаемых теоретических результатов. Вместо этого он дает действительно небольшие результаты и не приводит к классическим характеристикам интегратора (величина -20 дБ / декада и -90 градусов фаза) после обработки.

Может быть, несколько строк кода могут быть полезны, если я не достаточно ясно:

h = tf(1,[1 0]);
t_step = .1;
t = [0 : t_step : 100000]';
[y,t1] = impulse(h,t);
y_fft = fft(y);

Вы знаете, откуда может возникнуть эта проблема? Если вам нужна дополнительная информация, пожалуйста, дайте мне знать. Я работаю над MATLAB R2013b.

Answer 1

Как уже упоминалось в моем комментарии, проблема связана с:

1. fft предполагает периодический сигнал, то есть бесконечное повторение предоставленного дискретного сигнала
2. Вы должны также включить ответ для отрицательных времен, то есть до того, как импульс произошел.

---

h = tf(1,[1 0]);
t_step = 1;
t = [0 : t_step : 999]';
[y,t1] = impulse(h,t);

y = [y; zeros(1000, 1)];
y_fft = fft(y);

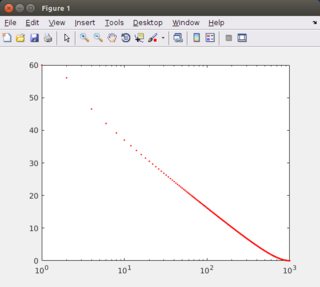
figure
semilogx(db(y_fft(1:end/2)), 'r.');

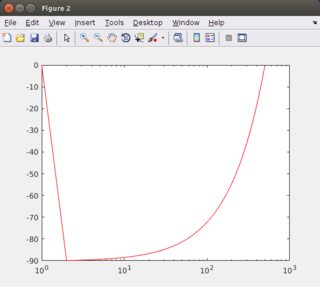
figure
semilogx(180/pi*angle(y_fft(y_fft(1:end/2)~=0)), 'r');

Дальнейшие замечания

• Обратите внимание, что из-за периодичности fft (и y) половина значений равна минус бесконечность, которую я не строил, чтобы получить более хороший результат.

• Обратите внимание, что влияние разности между БПФ и непрерывным преобразованием Фурье зависит от реального преобразования Фурье импульсного отклика. Особенно алиасинг может быть проблемой.