Разработайте КПК со всеми строками 0 и 1 так, чтобы число 1 было вдвое больше, чем 0

Question

Во время подготовки к последним экзаменам я нашел этот вопрос в " Теории автоматов, языке и вычислениях" Дж. Хопкрофта, Р. Мотвани, Дж. Уллмана на странице 222.

КПК должен принять строку, в которой число цифр 1 равно удвоенному числу 0, и, если я не ошибаюсь в вопросе, строка может иметь различную последовательность нулей и единиц в определенном порядке или в определенном порядке.

Мой первый подход к этой проблеме был разделить проблему на две части

1. КПК для строк, начинающихся с 0. (Например - 010111)
2. КПК для строк, начинающихся с 1. (Например - 110101)

Но разделение проблемы, похоже, не уменьшает сложность проблемы.

Какой должен быть подход к таким проблемам?

Answer 1

Неважно, начинается ли строка с 0 или 1, при решении этой проблемы следует иметь в виду, что мы должны нажимать одну 1 на каждые два 1-ов оверстека, если вершина стека равна 1 и аналогично, если мы встречаем 0 как вершину стека, тогда мы должны вытолкнуть его только при появлении второго 1 в строке. Этот мотив может быть легко достигнут с помощью двух состояний. Пусть состояния будут q0 и q1. Если мы находимся в состоянии q0, то это означает, что мы не встретили первую 1 пары, а состояние q1 означает, что мы уже встретили первую 1 пары. Различные переходы для КПК показаны ниже.

Пусть PDA будет P ({q0, q1}, {0, 1}, {0,1, z},, q0, z)

(q0,0, z) = {(q0, 0z)}

(q0,1, z) = {(q1, z)}

(q0,0,0) = {(q0, 00)}

(q0,1,0) = {(q1, 0)}

(q0,0,1) = {(q0, ε)}

(q0,1,1) = {(q1,1)}

(q1,0,0) = {(q1, 00)}

(q1,1,0) = {(q0, ε)}

(q1,0,1) = {(q1, ε)}

(q1,1,1) = {(q0, 11)}

(q0, ε, z) = {(q0, ε)}

Answer 2

Я знаю, что ему 5 лет, но, поскольку ответ не был принят, я решил, что поделюсь своим ответом и посмотрю, поможет ли он кому-нибудь (я уверен, что это можно упростить, но это была моя логика):

Определение КПК: P({S, M, Z, q1, F}, {0, 1}, {0, 1, $}, функция перехода, описанная ниже, S, {S, F})

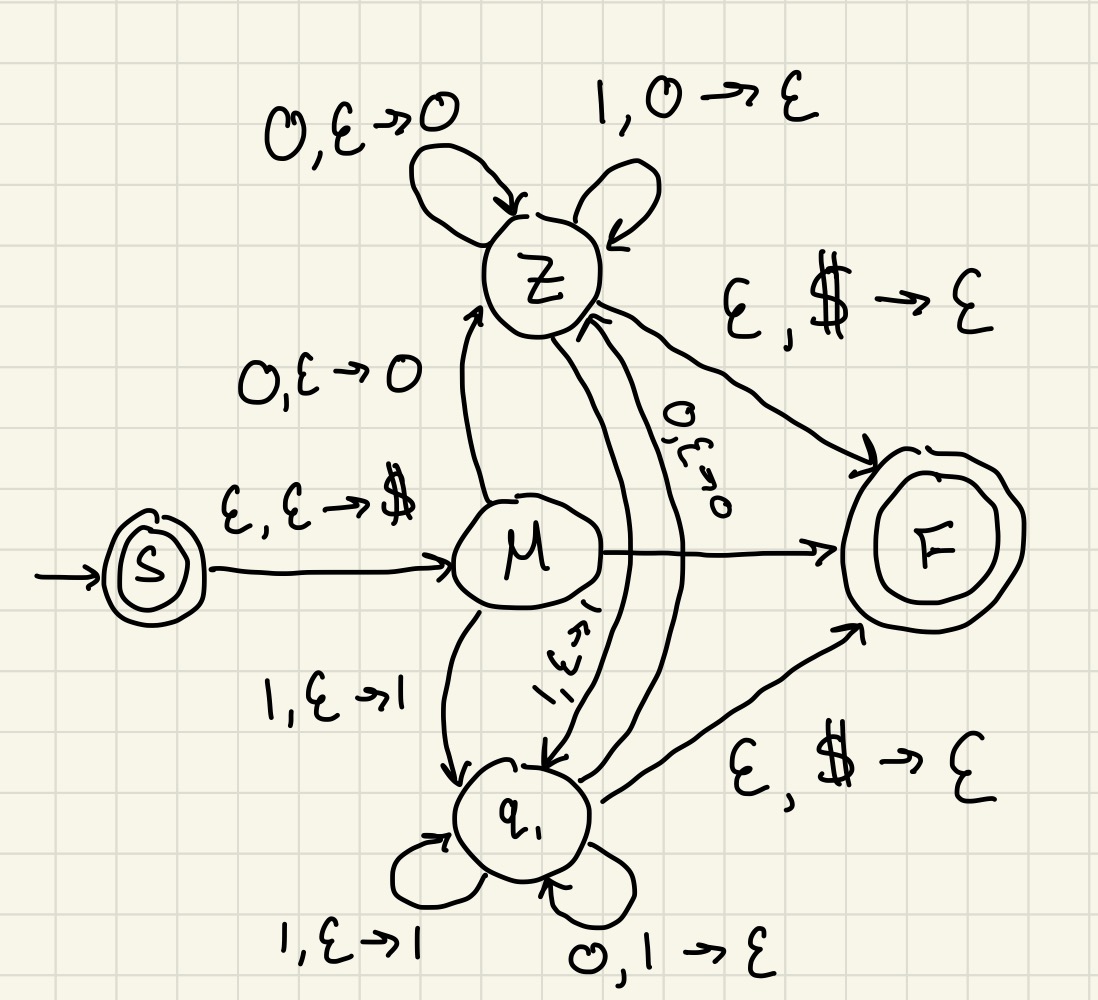
Я вставил изображение своего рисунка ниже, но сначала я поместил $ в стек, чтобы указать дно и перейти в состояние M. Затем, если первый символ был нулем, поместил ноль в стек и перешел в состояние z. Если это была единица, поместите 1 в стек и перейдите в состояние q1. В состоянии z, если следующий в строке стоит ноль, оставайтесь в состоянии z и добавьте ноль в стек. Если следующей в строке стоит 1, а наверху стека стоит ноль, вытолкните ноль из стека и оставайтесь в состоянии z. Если 1 стоит следующей в строке в состоянии z, а стек пуст, перейдите в состояние q1 и поместите 1 в стек. Если строка пуста и на вершине стека стоит символ $, то вытолкните $ и переместитесь в состояние F.

Состояние q1 имеет почти те же переходы, за исключением противоположного.

В состоянии q1, если единица стоит следующей в строке, оставаться в состоянии q1 и добавить единицу в стек. Если следующий в строке стоит ноль, а наверху стека стоит 1, вытолкните 1 из стека и оставайтесь в состоянии q1. Если 0 следующий в строке в состоянии q1, а стек пуст, перейдите в состояние z и поместите 0 в стек. Если строка пуста и на вершине стека стоит символ $, то вытолкните $ и переместитесь в состояние F.

Эта логика показана на рисунке ниже.

Answer 3

Еще два состояния должны быть добавлены с этим (q1,0,z) = {(q1, 0z)} и

(q1,1,z) = {(q1, 1z)}. Кроме того, для улучшения ответа сохраните отдельное конечное состояние, т.е. (q0,ε,z) = {(qf, ε)}, где qf - конечное состояние. Для проверки правильности можно использовать следующие строки (111100, 001111, 110110, 101110, 100111, 101011 и т. Д.)

Answer 4

Грамматика для языка, содержащего одинаковое количество нулей и единиц, является S -> 0S1S | 1S0S | epsilon

Точно так же грамматика для языка, содержащего в два раза больше единиц, чем нулей, являетсяS -> 0S1S1S | 1S0S1S | 1S1S0S | epsilon

Таким образом, NPDA будет выглядеть примерно так:

От q0 до q1: если вы читаете epsilon и увидеть z в верхней части стека нажмите S.

От q1 до q1: если вы читаете epsilon и увидите S вверху стека, нажмите 0S1S1S или толкнуть 1S0S1S или толкнуть 1S1S0Sили поп. Если вы читаете0 и увидеть 0вверху стопки - pop. Если вы читаете1 и увидеть 1 вверху стопки - pop.

От q1 до q2: если вы читаете epsilon и увидеть zвверху стопки - pop. q2 - конечное состояние.

Answer 5

Идея заключается в следующем:

Вставьте две 1 для каждого 0 или нажмите два 0 для каждого 0.

Вставьте один 0 для каждого 1 или нажмите один 1 для каждого 1.

Answer 6

У меня нет права комментировать, поэтому я прокомментирую здесь: я думаю, что ответ Дилраджа Сингха правильный, но с небольшой ошибкой печати: пусть КПК будет P ({q0, q1}, {0, 1}, {0 , 1, z}, 𝛿, q0, z)

𝛿 (q0,0, z) = {(q0, 0z)}

𝛿 (q0,1, z) = {(q1, z)}

𝛿 (q0,0,0) = {(q0, 00)}

𝛿 (q0,1,0) = {(q1, 0)}

𝛿 (q0,0,1) = {(q0, ε)}

𝛿 (q0,1,1) = {(q1,1)}

𝛿 (q1,0,0) = {(q1, 00)}

𝛿 (q1,1,0) = {(q0, ε)}

𝛿 (q1,0,1) = {(q1, ε)}

𝛿 (q1,1,1) = {(q0, 11)}

𝛿 (q1,0, z) = {(q1, 0z)}

𝛿 (q1,1, z) = {(q1, 1z)} // Я думаю, эта строка должна быть (q1,1, z) = {(q0, 1z)}

𝛿 (q0, ε,z) = {(q0, ε)}

Кроме того, я привожу соответствующую диаграмму:

схема вышеуказанного КПК

Если мой ответ вам поможет, проголосуйте за меня! Мне очень нужна репутация, чтобы комментировать и отправлять фотографии! XD