Почему мой анализатор рекурсивного спуска является ассоциативно-правым

Question

Я пишу свой собственный язык программирования, и у меня есть токенайзер (лексер). Но из-за разбора у меня возникли проблемы с написанием парсера рекурсивного спуска. Кажется, это право ассоциативно, когда его нужно оставить, и я не знаю почему. Например, он разбирает 1-2-3 как 1-(2-3)не правильно (1-2)-3,

Я обрезал большую часть другого кода, оставляя только то, что можно воспроизвести:

using System.Collections.Generic;

namespace Phi
{
    public enum TokenType
    {
        Plus, // '+'
        Minus, // '-'
        IntegerLiteral,
    }

    public interface INode
    {
        // Commented out as they aren't relevant
        //NodeType GetNodeType();
        //void Print(string indent, bool last);
    }

    class Program
    {
        static void Main(string[] args)
        {
            List<Token> tokens = new List<Token>()
            {
                new Token(TokenType.IntegerLiteral, "1"),
                new Token(TokenType.Minus, ""),
                new Token(TokenType.IntegerLiteral, "2"),
                new Token(TokenType.Minus, ""),
                new Token(TokenType.IntegerLiteral, "3"),
            };

            int consumed = ParseAdditiveExpression(tokens, out INode root);
        }

        private static int ParseAdditiveExpression(List<Token> block, out INode node)
        {
            // <additiveExpr> ::= <multiplicativeExpr> <additiveExprPrime>
            int consumed = ParseMultiplicataveExpression(block, out INode left);
            consumed += ParseAdditiveExpressionPrime(GetListSubset(block, consumed), out INode right);

            if (block[1].Type == TokenType.Plus)
                node = (right == null) ? left : new AdditionNode(left, right);
            else
                node = (right == null) ? left : new SubtractionNode(left, right);
            return consumed;
        }
        private static int ParseAdditiveExpressionPrime(List<Token> block, out INode node)
        {
            // <additiveExprPrime> ::= "+" <multiplicataveExpr> <additiveExprPrime>
            //                     ::= "-" <multiplicativeExpr> <additiveExprPrime>
            //                     ::= epsilon
            node = null;
            if (block.Count == 0)
                return 0;
            if (block[0].Type != TokenType.Plus && block[0].Type != TokenType.Minus)
                return 0;

            int consumed = 1 + ParseMultiplicataveExpression(GetListSubset(block, 1), out INode left);
            consumed += ParseAdditiveExpressionPrime(GetListSubset(block, consumed), out INode right);

            if (block[0].Type == TokenType.Plus)
                node = (right == null) ? left : new AdditionNode(left, right);
            else
                node = (right == null) ? left : new SubtractionNode(left, right);
            return consumed;
        }

        private static int ParseMultiplicataveExpression(List<Token> block, out INode node)
        {
            // <multiplicativeExpr> ::= <castExpr> <multiplicativeExprPrime>
            // unimplemented; all blocks are `Count == 1` with an integer
            node = new IntegerLiteralNode(block[0].Value);
            return 1;
        }

        private static List<T> GetListSubset<T>(List<T> list, int start)
        {
            return list.GetRange(start, list.Count - start);
        }
    }
}

Что касается определения AdditionNode, SubtractionNode, а также MultiplicationNodeони все одинаковы и служат только семантическим целям. Для краткости, вот только AdditionNode:

namespace Phi
{
    public class AdditionNode : INode
    {
        public AdditionNode(INode left, INode right)
        {
            Left = left;
            Right = right;
        }

        public INode Left { get; }
        public INode Right { get; }

        // Print and GetNodeType have been removed as they aren't relevant
    }
}

Что касается моей проблемы, когда я бегу Phi.ProgramКак уже говорилось в начале, он разбирается с неправильной ассоциативностью. Вот root после ParseAdditiveExpression завершается:

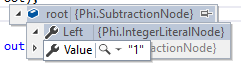
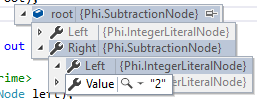
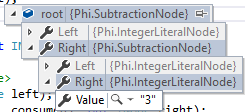
Как видите, он группирует 2 с 3, не 1, Почему он это делает?

Answer 1

Как я отмечал в комментарии, проблема в том, что вы перепутали самый правый дочерний элемент бинарного оператора с самым правым дочерним элементом аддитивного простого числа. Самый правый потомок бинарного оператора - это выражение. Самая правая сторона addprime - это addprime, поэтому на основании "типа узла дерева" мы должны сделать вывод, что вы создали неправильное дерево разбора.

Отслеживание "логического типа" каждого артефакта синтаксического анализа является мощной техникой для поиска ошибок в синтаксических анализаторах. Еще одна вещь, которая мне нравится и трагически недооценивается, - это приписывать каждый токен в программе ровно одному узлу дерева разбора. Если вы это сделаете, то быстро поймете, что токен для оператора логически находится в двух местах: в бинарном операторе и в его самом правом дочернем элементе. Это также говорит нам, что что-то не так.

Что не помогает, так это то, что ваша инфраструктура для разбора представляет собой ужасный беспорядок передачи чисел и параметров. Вашему парсеру не хватает дисциплины. Ваш код синтаксического анализатора выглядит так, будто подсчет токенов - это самая важная вещь, которую выполняет анализатор, а все остальное является случайным.

Синтаксический анализ - это очень четкая проблема, и методы синтаксического анализа должны выполнять одно, только одно, и делать это идеально. Структура синтаксического анализатора и структура каждого метода должны напрямую отражать анализируемую грамматику. В синтаксическом анализаторе не должно быть почти никакой арифметики целых чисел, поскольку синтаксический анализ заключается в построении дерева разбора, а не в подсчете токенов.

Я создаю парсеры рекурсивного спуска для жизни. Позвольте мне показать вам, как бы я создал этот парсер, если бы я строил его быстро для своих собственных целей. (Если бы я создавал его для производственного приложения, во многих отношениях он был бы другим, но здесь мы поймем это легко.)

---

Хорошо, начнем. Первое: когда вы застряли на проблеме, решите более простую проблему. Давайте упростим задачу следующим образом:

• Предположим, что поток токенов является правильно сформированной программой. Нет обнаружения ошибок.
• Токены - это строки.
• Грамматика это: E ::= T E', E' ::= + T E' | nil, а также T это термин, состоящий из одного токена.

Отлично. Начните с создания типов, которые представляют каждую из этих вещей.

sealed class Term : ParseTree 
{
    public string Value { get; private set; }
    public Term(string value) { this.Value = value; }
    public override string ToString() { return this.Value; }
}
sealed class Additive : ParseTree 
{ 
    public ParseTree Term { get; private set; }
    public ParseTree Prime { get; private set; }
    public Additive(ParseTree term, ParseTree prime) {
        this.Term = term;
        this.Prime = prime;
    }
    public override string ToString() { return "" + this.Term + this.Prime; }
}
sealed class AdditivePrime : ParseTree 
{ 
    public string Operator { get; private set; }
    public ParseTree Term { get; private set; }
    public ParseTree Prime { get; private set; }
    public AdditivePrime(string op, ParseTree term, ParseTree prime) {
        this.Operator = op;
        this.Term = term;
        this.Prime = prime;
    }
    public override string ToString() { return this.Operator + this.Term + this.Prime; }
}
sealed class Nil : ParseTree 
{
    public override string ToString() { return ""; }
}

Обратите внимание на несколько вещей:

• Абстрактные классы являются абстрактными.
• Конкретные классы герметичны.
• Все неизменно.
• Все умеют печатать сами.
• Нет нуля! НЕТ НУЛЕЙ. Нули вызывают сбои. У вас есть производство с именем nil, поэтому создайте тип с именем Nil представлять это.

Далее: как мы хотим, чтобы парсер выглядел с точки зрения пользователя? Нам нужна последовательность токенов, и мы хотим, чтобы появилось дерево разбора. Отлично. Таким образом, общественная поверхность должна быть:

sealed class Parser
{
    public Parser(List<string> tokens) { ... }
    public ParseTree Parse() { ... }
}

И если мы все сделали правильно, то сайт вызова выглядит так:

public static void Main()
{
    var tokens = new List<string>() { "1" , "+" , "2" , "+" , "3" , "+" , "4"};
    var parser = new Parser(tokens);
    var result = parser.Parse();
    System.Console.WriteLine(result);
}

Супер. Теперь все, что нам нужно сделать, это реализовать.

Парсер отслеживает список токенов и текущий токен на рассмотрении. Не проносите эту информацию от метода к методу. Это логически часть парсера, поэтому держите его в парсере.

public sealed class Parser
{
    private List<string> tokens;
    private int current;    
    public Parser(List<string> tokens)
    {
        this.tokens = tokens;
        this.current = 0;
    }

Язык состоит сейчас только из аддитивных выражений, поэтому:

    public ParseTree Parse()
    {
        return ParseAdditive();
    }

Отлично, мы уже сделали два члена парсера. Теперь, что делает ParseAdditive делать? Он делает то, что говорит на жестяной банке. Разбирает аддитивное выражение, которое имеет грамматику E:: T E', так что это то, что он делает, и ВСЕ, что он делает, на данный момент.

private ParseTree ParseAdditive()
{
    var term = ParseTerm();
    var prime = ParseAdditivePrime();
    return new Additive(term, prime);
}

Если ваши методы парсера не выглядят невероятно простыми, значит, вы делаете что-то не так. Смысл синтаксических анализаторов рекурсивного спуска в том, что они просты для понимания и реализации.

Теперь мы можем увидеть, как реализовать ParseTerm(); он просто потребляет токен:

private string Consume() 
{
  var t = this.tokens[this.current];
  this.current += 1;
  return t;
}
private ParseTree ParseTerm() {
  return new Term(Consume());
}

Опять же, мы предполагаем, что поток токенов хорошо сформирован. Конечно, это может привести к сбою, если он будет плохо сформирован, но это проблема для другого дня.

И, наконец, последний немного сложнее, потому что есть два случая.

private bool OutOfTokens() 
{
  return this.current >= this.tokens.Count;
}
private ParseTree ParseAdditivePrime()
{
    if (OutOfTokens())
        return new Nil();
    var op = Consume();
    var term = ParseTerm();
    var prime = ParseAdditivePrime();
    return new AdditivePrime(op, term, prime);
}

Так просто Опять же, все ваши методы должны выглядеть именно так, как они.

Обратите внимание, что я не писал

private ParseTree ParseAdditivePrime()
{
    if (this.current >= this.tokens.Count)
        return new Nil();

Сохраняйте текст программы как операции, которые она выполняет. Что мы хотим знать? У нас закончились жетоны? Так и говори. Не заставляйте читателя - себя - думать о, я имел в виду > или же < или же <= или... просто нет. Решите проблему один раз, поместите решение в метод с хорошим именем и затем вызовите метод. Ваше будущее я поблагодарит вас за то, что вы позаботились об этом.

Также обратите внимание, что я не написал супер-пятно C# 7:

private ParseTree ParseAdditivePrime() => 
  OutOfTokens() ? new Nil() : new AdditivePrime(Consume(), ParseTerm(), ParseAdditivePrime());

То, что вы можете написать свои методы синтаксического анализа как однострочные, является признаком того, что вы разработали хороший синтаксический анализатор, но это не означает, что вы должны это делать. Часто легче понять и отладить парсер, если вы сохраняете его в форме последовательных операторов, а не в виде маленьких строчек. Осуществлять здравый смысл.

---

ОК, мы решили более легкую проблему! Теперь давайте решим немного более сложную проблему. Мы решили разобрать грамматику E ::= T E', E' ::= + T E' | nil, но грамматика, которую мы хотим разобрать B :: T | B + T,

Обратите внимание, что я не путаю E , который является термином и суффиксом с B , который является либо T или B , + и T , поскольку B а также E разные, представляют их разными типами.

Давайте сделаем тип для B:

sealed class Binary : ParseTree 
{
    public ParseTree Left { get; private set; }
    public string Operator { get; private set; }
    public ParseTree Right { get; private set; }
    public Binary(ParseTree left, string op, ParseTree right) 
    {
        this.Left = left; 
        this.Operator = op;
        this.Right = right;
    }
    public override string ToString() 
    {
        return "(" + Left + Operator + Right + ")";
    }
}

Обратите внимание, что я добавил скобки в вывод в качестве наглядного пособия, чтобы помочь нам увидеть, что он оставлен ассоциативным.

Теперь предположим, что у нас есть Additive в руке, и нам нужен Binary, Как мы собираемся это сделать?

Добавка - это всегда термин и простое число. Итак, есть два случая. Либо простое число равно нулю, либо нет.

Если простое число равно нулю, то мы закончили: Term приемлемо, когда Binary требуется, поэтому мы можем просто вернуть срок.

Если простое число не равно нулю, то простое число равно op, term, prime. Каким-то образом мы должны получить Binary из этого. Двоичный файл нуждается в трех вещах. Помните, что мы привязываем каждый токен только к одному узлу, так что это поможет нам разобраться.

• У нас есть левый член от добавки.
• У нас есть наш оп с премьер.
• У нас есть правильный термин от простого числа.

Но это оставляет премьер премьер! Мы должны что-то сделать с этим. Давайте рассмотрим это. Опять же, есть два случая:

• Если простое число простого числа равно нулю, то результатом является двоичное число.
• Если простое число простого числа не равно нулю, то результатом является новый двоичный файл со старым двоичным файлом слева, и... подождите минуту, это тот же алгоритм, который мы только что описали для преобразования аддитивной системы в двоичный файл.

Мы только что обнаружили, что этот алгоритм является рекурсивным, и как только вы поймете, что написать его тривиально:

private static ParseTree AdditiveToBinary(ParseTree left, ParseTree prime) 
{
    if (prime is Nil) return left;
    var reallyprime = (AdditivePrime) prime;
    var binary = new Binary(left, reallyprime.Operator, reallyprime.Term);
    return AdditiveToBinary(binary, reallyprime.Prime);
}

И теперь мы модифицируем наши ParseAdditive:

private ParseTree ParseAdditive()
{
    var term = ParseTerm();
    var prime = ParseAdditivePrime();
    return AdditiveToBinary(term, prime);       
}     

И запустите это:

(((1+2)+3)+4)

И мы сделали.

Ну, не совсем. ParseAdditive больше не делает то, что говорит на банке! Это говорит ParseAdditive но это возвращает Binary,

На самом деле... нам нужно Additive вообще? Можем ли мы полностью исключить это из парсера? На самом деле мы могли бы; Теперь мы никогда не создаем экземпляр Additive так что его можно удалить, и ParseAdditive можно переименовать ParseBinary,

Это часто происходит при построении программ с использованием техники "решить более простую задачу". Вы в конечном итоге можете отказаться от своей предыдущей работы, и это здорово. Удаленный код не имеет ошибок.

• Упражнение: представление операторов в виде строк является грубым. Сделать Operator класс, аналогичный Term и метод, который анализирует операторы. Продолжайте повышать уровень абстракции анализатора от конкретных строк до бизнес-сферы анализатора. Аналогично с токенами; они не должны быть струнами.
• Упражнение: мы решили более сложную задачу, так что продолжайте. Теперь вы можете добавить умножение?
• Упражнение: Можете ли вы разобрать язык, который имеет сочетание левого и правого ассоциативных операторов?

---

Некоторые дополнительные мысли:

• Я полагаю, вы делаете это либо для собственного удовольствия, либо для школьного задания. Не копируйте, вставьте мою работу в ваше задание. Это академическое мошенничество. Не забудьте правильно приписать всю работу, когда вы отправляете ее, если эта работа не полностью ваша.

• Если вы делаете это для удовольствия, получайте удовольствие от разработки языка! Это хорошее хобби, и если вам действительно повезет, когда-нибудь кто-нибудь заплатит вам за это.

• Вы создаете свой собственный язык, поэтому вам не нужно повторять ошибки прошлого. Например, я замечаю, что ваши комментарии предполагают, что вы собираетесь добавить выражения приведения. Добро пожаловать в мир боли, если вы делаете это, как C, C++, C#, Java и так далее. Все эти языки должны иметь свои разборщики между (x)+y что означает "применить унарный плюс к у и бросить вещь x и добавить количество (x) в y ". Это большая боль. Рассмотрим лучший синтаксис для приведений, как as оператор. Кроме того, исследуйте значение броска; в C# приведение означает как "создать экземпляр другого типа, который представляет одно и то же значение", так и "я утверждаю, что тип среды выполнения этой вещи отличается от ее типа времени компиляции; throw, если я ошибаюсь". Эти операции совершенно разные, но у них одинаковый синтаксис. Все языки являются ответами на предыдущие языки, поэтому подумайте о том, что вам нравится, потому что это знакомо, потому что это хорошо.