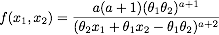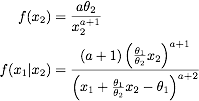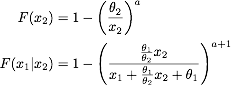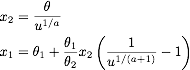Моделирование двумерного распределения Парето
Я ищу пакет / код, который бы генерировал двумерное распределение Парето, когда две случайные переменные коррелированы (и корреляция может быть указана пользователем). Буду благодарен за вашу помощь!
1 ответ
Я не смог найти какие-либо существующие пакеты R, но нашел ваш вопрос интересным; поэтому я хотел бы показать вам способ выборки из двумерного распределения Парето типа I с использованием выборки с обратным преобразованием.
теория
Совместный pdf двумерного распределения Парето типа I дается
Целью здесь является
- взять образцы для x2 из предельного распределения f (x2), а затем
- взять образцы для x1 заданного x2 из условного распределения f (x1 | x2).
Маргинальные и условные распределения задаются как (см., Например, [Mardia, Annals of Matetic Statistics 33, 1008 (1962)])
Мы можем нарисовать выборки, используя выборку с обратным преобразованием, которая требует кумулятивных функций распределения как для предельного, так и для условного распределения. Это легко рассчитать, и мы получаем
Тогда образцы для x1 и x2 задаются как
где u - случайное число из стандартного равномерного распределения в интервале [0,1].
Реализация R
Мы определяем две функции для выборки значений для x1 и x2 из маргинального и условного распределений, используя выборку с обратным преобразованием, как подробно описано выше.
rpareto_inv <- function(n, theta, a) { u <- runif(n, min = 0, max = 1); return(theta / (u ^ (1 / a))); } rpareto_cond_inv <- function(x2, theta1, theta2, a) { u <- runif(length(x2), min = 0, max = 1); return(theta1 + theta1 / theta2 * x2 * (1 / (u ^ (1 / (a + 1))) - 1)); }Мы выбрали несколько значений для параметров выборки и распределения:
n <- 10^5; # Number of samples theta1 <- 5; # Location parameter 1 theta2 <- 2; # Location parameter 2 a <- 3; # Shape parameterТеперь мы можем рисовать образцы
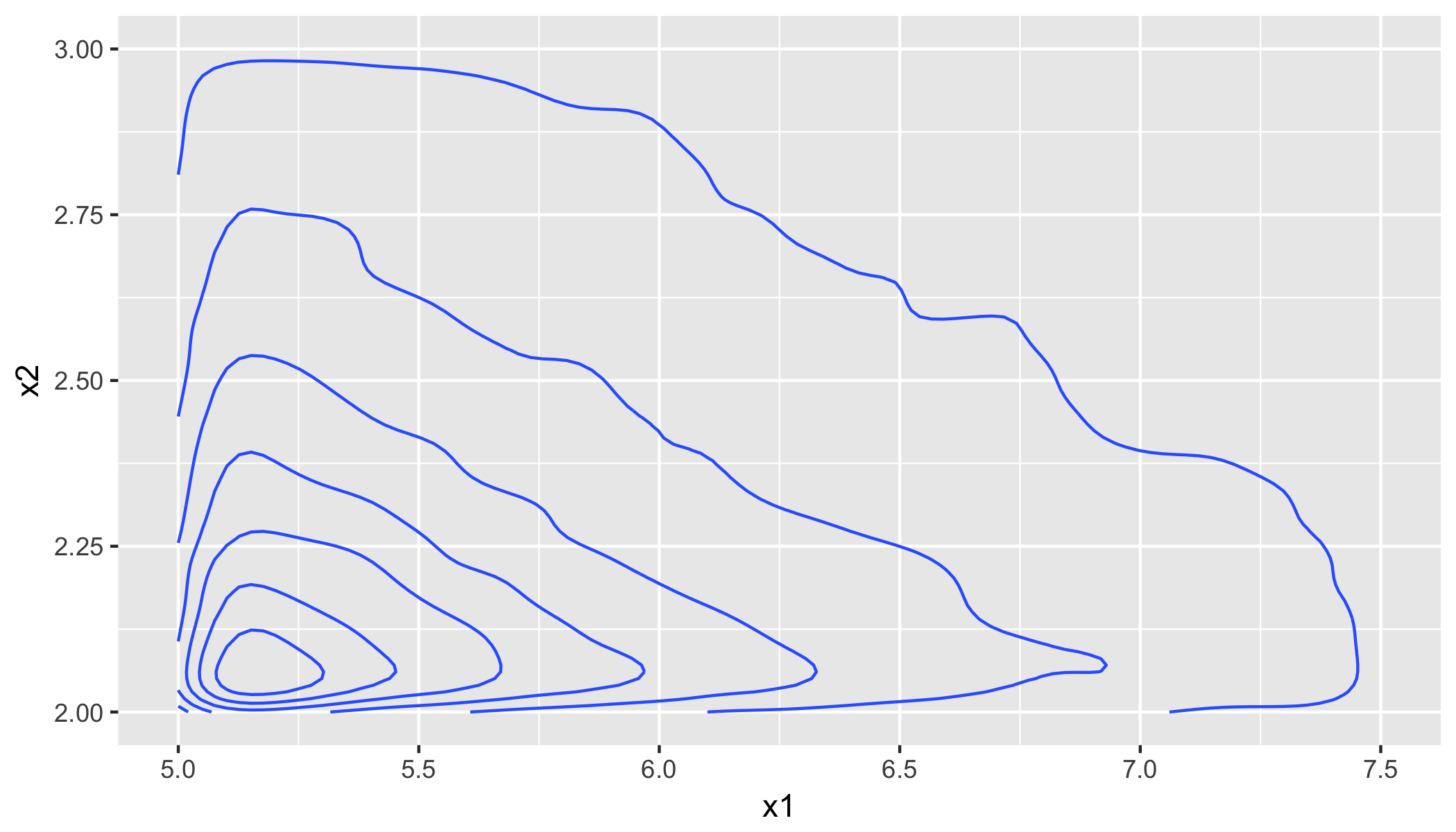
set.seed(2017); x2 <- rpareto_inv(n, theta = theta2, a = a); x1 <- rpareto_cond_inv(x2, theta1, theta2, a);Мы можем показать двухмерный график плотности и сравнить некоторые статистические данные выборки с их теоретическими (популяционными) значениями.
require(ggplot2); df <- cbind.data.frame(x1 = x1, x2 = x2); ggplot(df, aes(x1, x2)) + geom_density_2d() + xlim(theta1, 1.5 * theta1) + ylim(theta2, 1.5 * theta2);metrics <- cbind.data.frame( obsrv = c(mean(df$x1), mean(df$x2), cor(df$x1, df$x2), cov(df$x1, df$x2)), theor = c(a * theta1 / (a - 1), a * theta2 / (a - 1), 1/a, theta1 * theta2 / ((a - 1)^2 * (a - 2)))); rownames(metrics) <- c("Mean(x1)", "Mean(x2)", "Correlation", "Covariance") # obsrv theor #Mean(x1) 7.4947124 7.5000000 #Mean(x2) 3.0029318 3.0000000 #Correlation 0.3429634 0.3333333 #Covariance 2.3376545 2.5000000Вы можете видеть, что соглашение хорошее. Также отметим, что корреляция между x1 и x2 характеризуется параметром масштаба a. Следовательно, если вы хотите смоделировать данные для двумерного распределения Парето с определенной корреляцией r, вам просто нужно установить параметр формы в 1 / r. Более подробную информацию о распределении и дополнительных сводных статистических данных можно найти в [Mardia, Анналы математической статистики 33, 1008 (1962)].
Наконец, вы также можете использовать простой метод выборки принятия-отклонения, но я представляю, что он намного медленнее, чем метод выборки с обратным преобразованием, который я здесь показываю.