Какой самый эффективный способ сделать квадратный корень из суммы квадратов двух чисел?
Я ищу более эффективный и кратчайший способ выполнения квадратного корня из суммы квадратов из двух или более чисел. Я на самом деле использую numpy и этот код:
np.sqrt(i**2+j**2)
Это кажется в пять раз быстрее, чем:
np.sqrt(sum(np.square([i,j])))
(я и j к числам!)
Мне было интересно, есть ли уже встроенная функция, более эффективная для выполнения этой очень распространенной задачи с еще меньшим количеством кода.
5 ответов
Для случая i != j это невозможно сделать с np.linalg.normТаким образом, я рекомендую следующее:
(i*i + j*j)**0.5
Если i а также j одиночные поплавки, это примерно в 5 раз быстрее, чем np.sqrt(i**2+j**2), Если i а также j являются массивами, это примерно на 20% быстрее (из-за замены квадрата i*i а также j*j, Если вы не замените квадраты, производительность равна np.sqrt(i**2+j**2),
Некоторые тайминги с использованием одиночных поплавков:
i = 23.7
j = 7.5e7
%timeit np.sqrt(i**2 + j**2)
# 1.63 µs ± 15.6 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
%timeit (i*i + j*j)**0.5
# 336 ns ± 7.38 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
%timeit math.sqrt(i*i + j*j)
# 321 ns ± 8.21 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
math.sqrt немного быстрее чем (i*i + j*j)**0.5, но это происходит за счет потери гибкости: (i*i + j*j)**0.5 будет работать на одиночных поплавках и массивах, тогда как math.sqrt будет работать только на скалярах.
И немного времени для массивов среднего размера:
i = np.random.rand(100000)
j = np.random.rand(100000)
%timeit np.sqrt(i**2 + j**2)
# 1.45 ms ± 314 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
%timeit (i*i + j*j)**0.5
# 1.21 ms ± 78.8 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
Вместо того, чтобы оптимизировать этот довольно простой вызов функции, вы можете попробовать переписать вашу программу так, чтобы i а также j являются массивами вместо отдельных чисел (при условии, что вам нужно вызывать функцию для множества разных входов). Посмотрите на этот небольшой тест:
import numpy as np
i = np.arange(10000)
j = np.arange(10000)
%%timeit
np.sqrt(i**2+j**2)
# 74.1 µs ± 2.74 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
%%timeit
for idx in range(len(i)):
np.sqrt(i[idx]**2+j[idx]**2)
# 25.2 ms ± 1.8 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Как вы можете видеть, первый вариант (с использованием массивов чисел в качестве входных данных) примерно в 300 раз быстрее, чем второй, использующий цикл для Python. Причина этого заключается в том, что в первом примере все вычисления выполняются с помощью numpy (который реализован внутри c и, следовательно, действительно быстро), тогда как во втором примере чередуются код numpy и обычный код Python (цикл for), что делает выполнение намного медленнее.
Если вы действительно хотите улучшить производительность своей программы, я бы предложил переписать ее так, чтобы вы могли выполнять свою функцию один раз для двух массивов с нулевыми значениями вместо вызова ее для каждой пары чисел.
Я понимаю, что вам нужна скорость, но я хотел бы указать на некоторые недостатки написания собственного калькулятора sqroot
Сравнение скорости
%%timeit
math.hypot(i, j)
# 85.2 ns ± 1.03 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)
%%timeit
np.hypot(i, j)
# 1.29 µs ± 13.2 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
%%timeit
np.sqrt(i**2+j**2)
# 1.3 µs ± 9.87 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
%%timeit
(i*i + j*j)**0.5
# 94 ns ± 1.61 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)
По скорости оба numpy одинаковы, но гипотеза очень безопасна. По сути переливается. гипотеза эффективна - это чувство точности: p
Также math.hypot также очень безопасен и быстр и может обрабатывать 3d sqrt суммы sqrs и быстрее, чем
(i*i + j*j)**0.5
Недополнение
i, j = 1e-200, 1e-200
np.sqrt(i**2+j**2)
# 0.0
Переполнение
i, j = 1e+200, 1e+200
np.sqrt(i**2+j**2)
# inf
Нет переполнения
i, j = 1e-200, 1e-200
np.hypot(i, j)
# 1.414213562373095e-200
Нет переполнения
i, j = 1e+200, 1e+200
np.hypot(i, j)
# 1.414213562373095e+200
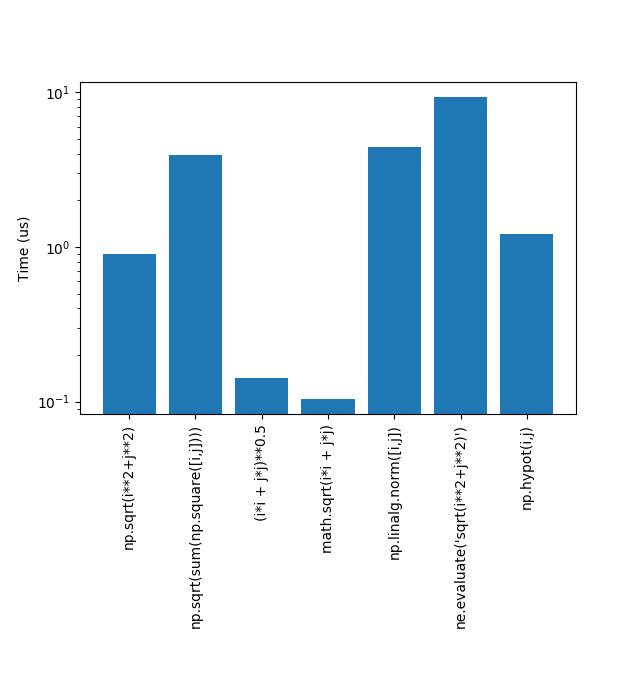
Я сделал некоторые сравнения на основе ответов, кажется, что более быстрый способ заключается в использовании math модуль, а затем math.sqrt(i*i + j*j) но, вероятно, лучшим компромиссом является использование (i*i + j*j)**0.5 без импорта какого-либо модуля, хотя и не так явно.
Код
from timeit import timeit
import matplotlib.pyplot as plt
tests = [
"np.sqrt(i**2+j**2)",
"np.sqrt(sum(np.square([i,j])))",
"(i*i + j*j)**0.5",
"math.sqrt(i*i + j*j)",
"np.linalg.norm([i,j])",
"ne.evaluate('sqrt(i**2+j**2)')",
"np.hypot(i,j)"]
results = []
for test in tests:
results.append(timeit(test,setup='i = 7; j = 4;\
import numpy as np; \
import math; \
import numexpr as ne', number=1000000))
lengths.append(len(test))
indx = range(len(results))
plt.bar(indx,results)
plt.xticks(indx,tests,rotation=90)
plt.yscale('log')
plt.ylabel('Time (us)')
В этом случае numexpr модуль может быть быстрее. Этот модуль избегает промежуточной буферизации и, следовательно, быстрее для определенных операций:
i = np.random.rand(100000)
j = np.random.rand(100000)
%timeit np.sqrt(i**2 + j**2)
# 1.34 ms
import numexpr as ne
%timeit ne.evaluate('sqrt(i**2+j**2)')
#370 us