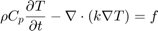Использование зависящего от времени (теплового) источника в PDE Toolbox

Question

Моя цель - применять зависящий от времени источник тепла при решении задачи теплообмена.

Дифференциальное уравнение в частных производных для переходного теплопередачи:

и больше информации можно найти здесь: Решение проблемы теплопередачи с температурозависимыми свойствами

Все параметры являются константами в моем случае, кроме исходного термина f, который необходимо менять вместе со временем.

Я следую приведенному здесь примеру кода: Нелинейная теплопередача в тонкой пластине, которая дает способ решить переходную проблему, и я могу построить данные о теплоте в каждый момент времени.

Проблема при применении его к моему случаю состоит в том, что в примере источник является постоянным значением во всем регионе и в течение всего времени и связан с излучением и конвекцией (в моем случае все они должны быть равны нулю), но мне нужно подача источника, зависящего от времени (джоулево нагревание изменяющимся во времени электрическим током). Источник может иметь один из следующих форматов:

1. Аналитический: положительное значение, такое как 1 Вт / м ^2, в пределах временного окна, например 0
2. Числовой: данные представлены вектором 1xN, где N - количество временных точек.

И источник ограничен определенным регионом, например. 0<х <1 мм и 0 <у <1 мм.

Я видел похожий вопрос, но без ответа: как использовать переменный коэффициент в PDE Toolbox для решения параболического уравнения (Matlab)

Есть ли способ реализовать это с помощью PDE Toolbox? Написание кода с нуля было бы так сложно....

Answer 1

Вы можете довольно легко определять и решать проблемы с зависящими от времени и нелинейными коэффициентами PDE с помощью FEATool FEM Matlab Toolbox, как показано здесь во фрагменте кода m-script ниже. Обратите внимание, что член f источника тепла (теплоотвода) масштабируется как f*(t>2500) Это означает, что он будет активен только после t=2500 (поскольку выражение переключателя оценивается либо в 0, если ложь, либо в 1, если истина).

% Coefficents and problem definition from https://www.mathworks.com/help/pde/examples/nonlinear-heat-transfer-in-a-thin-plate.html
k=400;rho=8960;specificHeat=386;thick=.01;stefanBoltz=5.670373e-8;hCoeff=1;ta=300;emiss=.5;

% Set up 2D fea struct with geometry and grid.
fea.sdim = {'x' 'y'};
fea.geom = { gobj_rectangle( 0, 1, 0, 1 ) };
fea.grid = rectgrid( 10 );

% Add heat transfer physics mode.
fea = addphys( fea, @heattransfer );

fea.phys.ht.eqn.coef{1,end}{1} = rho*thick;      % Density eqn coefficient.
fea.phys.ht.eqn.coef{2,end}{1} = specificHeat;   % C_p eqn coefficient.
fea.phys.ht.eqn.coef{3,end}{1} = k*thick;        % Thermal condictivity.
f = sprintf( '%g*( %g - T ) + %g*( %g^4 - T^4 )', ...
             2*hCoeff, ta, 2*emiss*stefanBoltz, ta );
fea.phys.ht.eqn.coef{6,end}{1} = ['(',f,')*(t>2500)'];   % Heat source term.

fea.phys.ht.bdr.sel(1) = 1;  % Set prescribed temperature for boundary 1.
fea.phys.ht.bdr.coef{1,end}{1} = 1000;  
fea.phys.ht.bdr.sel(2:4) = 3;   % Isolation BCs for boundaries 2-4.

% Check, parse, and solve fea problem.
fea = parsephys( fea );
fea = parseprob( fea );
[fea.sol.u,t] = solvetime( fea, 'tstep', 50, 'tmax', 5000, 'init', {ta} );

% Postprocessing and visualization.
for i=1:size(fea.sol.u,2)
  T_top(i) = evalexpr( 'T', [.5;1-sqrt(eps)], fea, i );
end

subplot(1,2,1)
postplot( fea, 'surfexpr', 'T', 'title', 'T @ t=5000' )
subplot(1,2,2)
plot( t, T_top, 'r-' )
xlabel( 't' )
ylabel( 'T(0.5,1) @ t=5000' )
grid on

В этом решении вы можете видеть, что температура верхнего края линейно возрастает из-за диффузии тепла от нижней границы до t=2500, где активируется теплоотвод.

Matlab FEATool Нелинейное зависящее от времени решение для теплопередачи

Что касается вашего второго пункта с числовым исходным термином, вы можете в этом случае создать и вызвать свою собственную внешнюю функцию, которая табулирует и интерполирует ваши данные, в этом случае это будет выглядеть примерно так

fea.phys.ht.eqn.coef{6,end}{1} = 'my_fun( t )';

где у вас есть функция Matlab my_fun.m где-то доступно на пути Matlab вида

function [ val ] = my_fun( t )
data  = [7 42 -100  0.1];   % Example data.
times = [0 10   99 5000];   % Time points.
val = interp1( data, times, t );   % Interpolate data.

И наконец, хотя модель определяется с использованием кода Matlab для m-скрипта, который здесь используется для совместного использования в Stackru, вы также можете легко использовать графический интерфейс Matlab FEA и даже экспортировать модель GUI в виде кода m-скрипта, если это необходимо.