Как мы предсказываем новые невидимые группы в иерархической модели в PyMC3?

Question

Если у нас есть иерархическая модель с данными из разных сайтов как разных групп в модели, как мы прогнозируем для новых групп (новых сайтов, которые мы раньше не видели)? например, используя следующую модель логистической регрессии:

from pymc3 import Model, sample, Normal, HalfCauchy,Bernoulli
import theano.tensor as tt
with Model() as varying_slope:

    mu_beta = Normal('mu_beta', mu=0., sd=1e5)
    sigma_beta = HalfCauchy('sigma_beta', 5)
    a = Normal('a', mu=0., sd=1e5)
    betas = Normal('b',mu=mu_beta,sd=sigma_beta,shape=(n_features,n_site))
    y_hat = a + tt.dot(X_shared,betas[:,site_shared])
    y_like = Bernoulli('y_like', logit_p=y_hat, observed=train_y)

После того, как мы подходим к этой модели, мы можем прогнозировать новые данные (то есть выборку из апостериорного прогнозирования) с определенного сайта, используя:

site_to_predict = 1
samples = 500

x = tt.matrix('X',dtype='float64')
new_site = tt.vector('new_site',dtype='int32')
n_samples = tt.iscalar('n_samples')
x.tag.test_value = np.empty(shape=(1,X.shape[1]))
new_site.tag.test_value = np.empty(shape=(1,1))

_sample_proba =  approx.sample_node(varying_slope.y_like.distribution.p,
                               size=n_samples,
                               more_replacements={X_shared: x,site_shared:new_site})

sample_proba = theano.function([x,new_site,n_samples], _sample_proba)

pred_test = sample_proba(test_X.reshape(1,-1),np.array(site_to_predict).reshape(-1),samples)

но как правильно выбрать выборку из апостериорного предиктивного распределения, если у нас есть новый невидимый сайт?

Answer 1

Я просто копирую свой ответ из ветки дискурса pymc, если кто-то случайно натолкнется на этот вопрос или другой, как он здесь.

Прежде всего, остерегайтесь используемой центрированной иерархической параметризации 1, это может привести к расхождениям и трудностям при подгонке.

Тем не менее, ваша модель выглядит более или менее как GLM с общими предыдущими случайными вариациями mu_beta и sigma_beta по функциям и сайтам. Как только вы получите апостериорное распределение по этим двум, ваши прогнозы должны выглядеть примерно так:

y_hat = a + dot(X_shared, Normal(mu=mu_beta, sigma=sigma_beta))
y_like = Bernoulli('y_like', logit_p=y_hat)

Итак, мы стремимся получить это.

Способ, которым мы всегда рекомендуем из выборочных апостериорных прогностических проверок, заключается в использовании theano.shared's. Я буду использовать другой подход, основанный на функциональном API, который является основной идеей дизайна для pymc4. Существует много различий между pymc3 и каркасом pymc4, но я начал использовать больше, это фабричные функции для получения экземпляров Model. Вместо того, чтобы пытаться определять вещи внутри модели с помощью theano.shared, я просто создаю новую модель с новыми данными и извлекаю из нее апостериорные прогностические выборки. Я только недавно написал об этом здесь.

Идея состоит в том, чтобы создать модель с тренировочными данными и выборкой из нее, чтобы получить трассировку. Затем вы должны извлечь из трассировки иерархическую часть, которая используется совместно с невидимым сайтом: mu_beta, sigma_beta и a. Наконец, вы создаете новую модель, используя новые данные тестового сайта, и производите выборку из апостериорного прогнозирования, используя список словарей, которые содержат mu_beta, sigma_beta и часть обучающей трассы. Вот автономный пример

import numpy as np
import pymc3 as pm
from theano import tensor as tt
from matplotlib import pyplot as plt


def model_factory(X, y, site_shared, n_site, n_features=None):
    if n_features is None:
        n_features = X.shape[-1]
    with pm.Model() as model:
        mu_beta = pm.Normal('mu_beta', mu=0., sd=1)
        sigma_beta = pm.HalfCauchy('sigma_beta', 5)
        a = pm.Normal('a', mu=0., sd=1)
        b = pm.Normal('b', mu=0, sd=1, shape=(n_features, n_site))
        betas = mu_beta + sigma_beta * b
        y_hat = a + tt.dot(X, betas[:, site_shared])
        pm.Bernoulli('y_like', logit_p=y_hat, observed=y)
    return model


# First I generate some training X data
n_features = 10
ntrain_site = 5
ntrain_obs = 100
ntest_site = 1
ntest_obs = 1
train_X = np.random.randn(ntrain_obs, n_features)
train_site_shared = np.random.randint(ntrain_site, size=ntrain_obs)
new_site_X = np.random.randn(ntest_obs, n_features)
test_site_shared = np.zeros(ntest_obs, dtype=np.int32)
# Now I generate the training and test y data with a sample from the prior
with model_factory(X=train_X,
                   y=np.empty(ntrain_obs, dtype=np.int32),
                   site_shared=train_site_shared,
                   n_site=ntrain_site) as train_y_generator:
    train_Y = pm.sample_prior_predictive(1, vars=['y_like'])['y_like'][0]
with model_factory(X=new_site_X,
                   y=np.empty(ntest_obs, dtype=np.int32),
                   site_shared=test_site_shared,
                   n_site=ntest_site) as test_y_generator:
    new_site_Y = pm.sample_prior_predictive(1, vars=['y_like'])['y_like'][0]

# The previous part is just to get some toy data to fit
# Now comes the important parts. First training
with model_factory(X=train_X,
                   y=train_Y,
                   site_shared=train_site_shared,
                   n_site=ntrain_site) as train_model:
    train_trace = pm.sample()

# Second comes the hold out data posterior predictive
with model_factory(X=new_site_X,
                   y=new_site_Y,
                   site_shared=test_site_shared,
                   n_site=ntrain_site) as test_model:
    # We first have to extract the learnt global effect from the train_trace
    df = pm.trace_to_dataframe(train_trace,
                               varnames=['mu_beta', 'sigma_beta', 'a'],
                               include_transformed=True)
    # We have to supply the samples kwarg because it cannot be inferred if the
    # input trace is not a MultiTrace instance
    ppc = pm.sample_posterior_predictive(trace=df.to_dict('records'),
                                         samples=len(df))
    plt.figure()
    plt.hist(ppc['y_like'], 30)
    plt.axvline(new_site_Y, linestyle='--', color='r')

Апостериорный прогноз, который я получаю, выглядит так: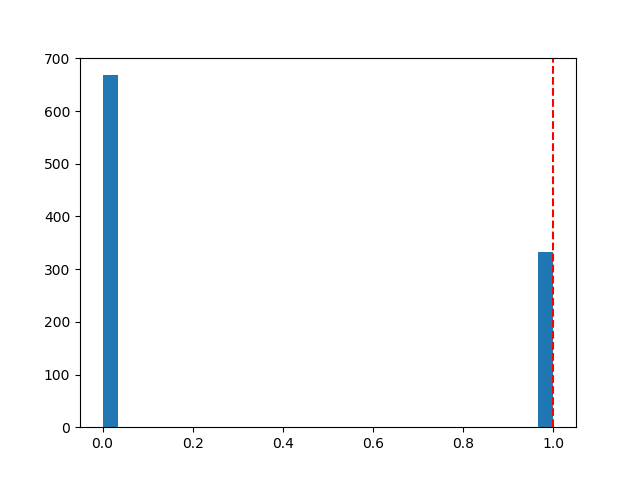

Конечно, я не знаю, какие именно данные нужно конкретно указать как ваши X_shared, site_shared или train_y, поэтому я просто собрал некоторые бессмысленные игрушечные данные в начале кода, вы должны заменить их фактическими данными.