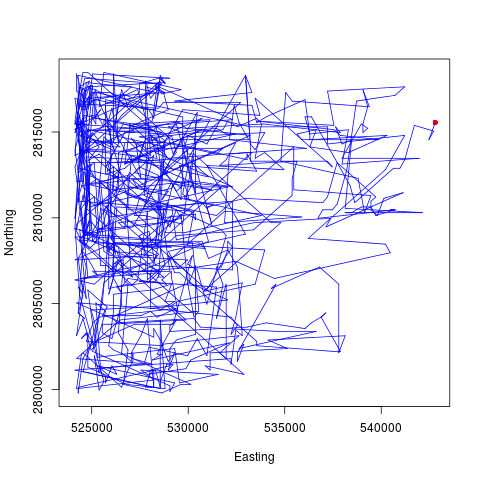
Как мне установить пределы арены при случайной прогулке?

Question

Я строю предвзятую коррелированную случайную прогулку, и мне удалось построить RW и сместить его для западного движения.

Вопрос: мне нужно, чтобы прогулка была связана с одной (или всеми) сторонами.

Текущий код:

walk<-function(n.times){ 
   plot(524058:542800,2799758:2818500,type="n",
      xlab="Easting",ylab="Northing")#aren‌​a 
      y<-2815550 ##startY 
      x<-542800 #startX
      N<-4000
      E<-4000
      points(x,y,pch=16,col="red",cex=1)
      for (i in 1:n.times) {
          yi <- sample(c(N,N/2,N/4,N/8,N/12,N/16,
                      0,-N,-N/2,-N/4,-N/8,-N/12,-N/16),1)      
          xi<-sample(c(E,E/12,E/16, 0,-E,-E/2,-E/4,-E/8,-E/12,-E/16),1)       
          lines(c(x,x+xi),c(y,y+yi),col="blue")
          x<-x+xi
          y<-y+yi 
      }
   }
   iterations<-125 
   walk(iterations) 

Пока самое близкое, что я пришел, использует

 if(y>2818500 | y<2799758 | x>542800 | x<524058)  break 

который просто останавливает прогулку, если покидает арену.

Answer 1

Немного очищенная версия функции: основное изменение - добавление repeat {} цикл, который будет перебирать шаг до тех пор, пока новое местоположение не будет в пределах (можно также использовать while() {} петля).

обновление: недостаточно внимательно прочитал формулировку проблемы, забыл предвзятость. Этот код включает смещение таким же образом, как и код OP. Для движения NS средняя длина шага равна 0; для движения EW, упуская некоторые положительные возможности шага, мы получаем mean(steps.x) равен -0,0875; поскольку возможности шага выбираются равномерно, прогулка смещается влево в среднем на 0.0875*stepsize[1] единиц на шаг.

 walk <- function(n.times=125,
               xlim=c(524058,542800),
               ylim=c(2799758,2818500),
               start=c(542800,2815550),
               stepsize=c(4000,4000)) {
    ## blank plot of arena
    plot(c(0,0),type="n",xlim=xlim,ylim=ylim,
           xlab="Easting",ylab="Northing") 
    ## extract starting point
    x <- start[1]
    y <- start[2]
    ## define potential step sizes
    steps <- 1/c(1,2,4,8,12,16)
    ## all possible positive or negative steps for N-S movement
    steps.y <- c(steps,-steps,0)
    ## bias E-W movement by leaving out some positive steps
    steps.x <- c(steps[c(1,5,6)],-steps,0)
    ## plot starting location
    points(x,y,pch=16,col="red",cex=1)
    for (i in 1:n.times) {
        repeat {
           ## pick jump sizes
           xi <- stepsize[1]*sample(steps.x,1)
           yi <- stepsize[2]*sample(steps.y,1)
           ## new candidate locations
           newx <- x+xi
           newy <- y+yi
           ## IF new locations are within bounds, then
           ##    break out of the repeat{} loop (otherwise
           ##    try again)
           if (newx>xlim[1] && newx<xlim[2] &&
               newy>ylim[1] && newy<ylim[2]) break
        }
        lines(c(x,newx),c(y,newy),col="blue") ## draw move
        ## set new location to candidate location
        x <- newx
        y <- newy
    }
}
set.seed(101)
walk(1000)