Как определить размер тестовой партии, чтобы полностью использовать NVIDIA Titan X

Question

При обучении модели глубокого обучения я обнаружил, что графический процессор используется не полностью, если я установил поезд и проверил (проверил) размер партии на одинаковый, скажем, 32, 64, ..., 512.

Затем я проверяю спецификации NVIDIA Titan X:

1. NVIDIA CUDA® Cores: 3584
2. Память: 12 ГБ GDDR5X

Чтобы сократить время тестирования для модели CNN, я хочу максимально увеличить количество выборок в партии. Я старался:

• установите количество выборок на партию 3584, из-за ошибки памяти.
• установите количество сэмплов на партию 2048, из-за ошибки памяти.
• установить количество образцов на партию до 1024, работает. но я не уверен, полностью ли используется графический процессор или нет.

Вопрос:

Как легко выбрать количество выборок на партию, чтобы полностью использовать графический процессор при глубокой модели прямой работы?

Answer 1

Использование watch nvidia-smi чтобы проверить, сколько памяти GPU используют ваши процессы.

FYI:

• Конфигурирование Theano так, чтобы оно не зависало напрямую при сбое выделения памяти графическим процессором
• Соотношение размера пакета и количества итераций для обучения нейронной сети:

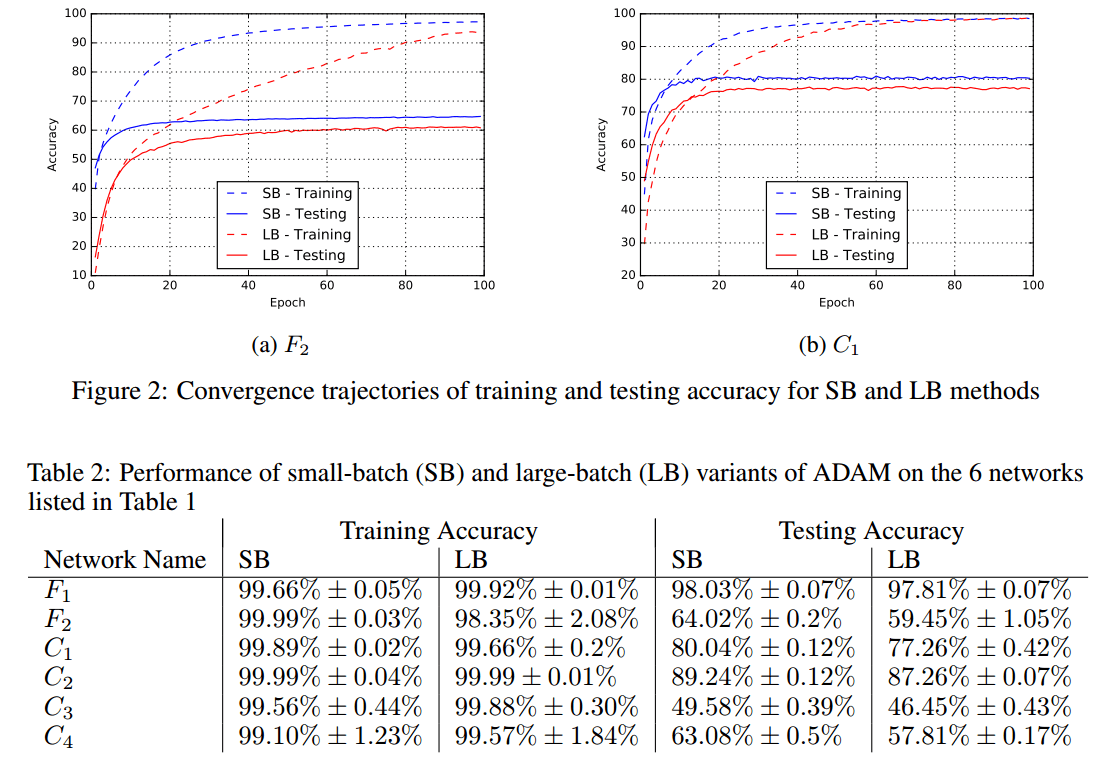
Из Нитиш Шириш Кескар, Дхиватса Мудигере, Хорхе Носедал, Михаила Смелянского, Пинг Так Питер Танг. О крупномасштабном обучении для глубокого обучения: разрыв в обобщении и острые минимумы. https://arxiv.org/abs/1609.04836:

Метод стохастического градиентного спуска и его варианты являются алгоритмами выбора для многих задач глубокого обучения. Эти методы работают в режиме малой партии, когда часть обучающих данных, обычно 32-512 точек данных, отбирается для вычисления приближения к градиенту. На практике наблюдалось, что при использовании более крупной партии качество модели значительно ухудшается, что измеряется ее способностью к обобщению. Были предприняты некоторые попытки исследовать причину такого обобщения в режиме больших партий, однако точный ответ для этого явления до сих пор неизвестен. В этой статье мы представляем достаточно числовых доказательств, подтверждающих мнение о том, что методы больших партий имеют тенденцию сходиться к точным минимизаторам функций обучения и тестирования - и что острые минимумы приводят к худшему обобщению. Напротив, мелкосерийные методы постоянно сходятся к плоским минимизаторам, и наши эксперименты подтверждают широко распространенное мнение о том, что это происходит из-за собственного шума при оценке градиента. Мы также обсуждаем несколько эмпирических стратегий, которые помогают методам больших партий устранить пробел в обобщении и завершить с набором будущих идей исследования и открытых вопросов.

[...]

Отсутствие способности к обобщению связано с тем, что методы больших партий имеют тенденцию сходиться к резким минимизаторам обучающей функции. Эти минимизаторы характеризуются большими положительными собственными значениями в $\nabla^2 f(x)$ и имеют тенденцию обобщать менее хорошо. Напротив, мелкосерийные методы сходятся к плоским минимизаторам, характеризующимся небольшими положительными собственными значениями $\nabla^2 f(x)$. Мы наблюдали, что ландшафт функций потерь глубоких нейронных сетей таков, что методы больших партий почти неизменно притягиваются к областям с резкими минимумами и что, в отличие от методов небольших партий, не могут покинуть бассейны этих минимизаторов.

[...]