Сохраните ориентацию к массиву - и сравните

Я хочу добиться следующего:

Я хочу, чтобы пользователь мог "записывать" движение iPhone с помощью гироскопа. И после этого пользователь должен иметь возможность повторить то же движение. Я извлекаю поле, крен и рыскание, используя:

 [self.motionManager startDeviceMotionUpdatesToQueue:[NSOperationQueue currentQueue]
                                       withHandler: ^(CMDeviceMotion *motion, NSError *error)
     {
         CMAttitude *attitude = motion.attitude;
         NSLog(@"pitch: %f, roll: %f, yaw: %f]", attitude.pitch, attitude.roll, attitude.yaw);
     }];

Я думаю, что я мог бы сохранить эти значения в массиве, если пользователь находится в режиме записи. И когда пользователь пытается воспроизвести это движение, я могу сравнить реплицированный массив движений с записанным. Дело в том, как я могу разумно сравнить два массива? Они никогда не будут иметь одинаковые значения, но они могут быть примерно одинаковыми.

Я на правильном пути?

ОБНОВЛЕНИЕ: Я думаю, что, возможно, ответ Алиса об использовании DTW может быть правильным для меня здесь. Но я не такой умный (по-видимому), поэтому, если бы кто-нибудь мог помочь мне с первыми шагами по сравнению с массивами, я был бы счастливым человеком!

Спасибо!

Источник

2 ответа

Решение

Попробуйте динамическое искажение времени. Вот иллюстративный пример с 1D массивами. В базе данных у нас уже есть следующие 2 массива:

Массив 1: [5, 3, 1]
Массив 2: [1, 3, 5, 8, 8]

Мы измерили [2, 4, 6, 7], Какой массив наиболее похож на недавно измеренный? Очевидно, что второй массив похож на вновь измеренный, а первый - нет.

Давайте вычислим матрицы затрат согласно этой статье, подраздел 2.1:

D(i,j)=Dist(i,j)+MIN(D(i-1,j),D(i,j-1),D(i-1,j-1))

Вот D(i,j) это (i,j) элемент матрицы затрат, см. ниже. Проверьте рисунок 3 этого документа, чтобы увидеть, что это рекуррентное отношение применяется. Вкратце: столбцы вычисляются первыми, начиная с D(1,1); D(0,*) а также D(*,0) опущены в мин. Если мы сравниваем массивы A а также B затем Dist(i,j) это расстояние между A[i] а также B[j], Я просто использовал ABS(A[i]-B[j]), Матрицы стоимости для этого примера:

Динамическая Деформация Времени, матрицы затрат

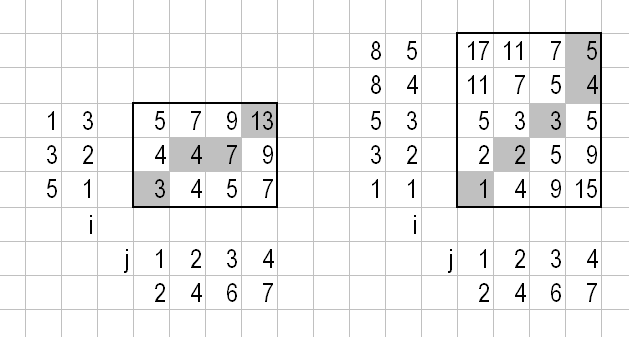
Для массива 1 у нас 13 баллов, для массива 2 - 5. Побеждает меньший балл, поэтому наиболее похожим массивом является массив 2. Лучший путь деформации отмечен серым.

Это всего лишь набросок DTW. Есть ряд проблем, которые вы должны решить в реальном приложении. Например, использование смещения вместо фиксированных конечных точек или определение мер подгонки: см. Этот документ, стр. 363, 5. граничные условия и стр. 364. В приведенном выше связанном документе также есть дополнительные сведения.

Я только что заметил, что вы используете рыскание, тангаж и крен. Проще говоря: нет, и еще одна причина не делать этого. Можете ли вы использовать данные акселерометра вместо этого? "Акселерометр - это прямое измерение ориентации" (из рукописи DCM), и это то, что вам нужно. А что касается вопроса ТС, имеет ли значение ориентация относительно Севера? Я думаю, нет.

Гораздо проще сравнивать векторы ускорения, чем ориентации (углы Эйлера, матрицы вращения, кватернионы), как указало tc. Если вы используете данные ускорения, у вас есть 3-мерные векторы в каждый момент времени, координаты (x,y,z). Я бы просто вычислил

Dist(i,j)=SQRT((A[i][X]-B[j][X])^2+(A[i][Y]-B[j][Y])^2+(A[i][Z]-B[j][Z])^2),

это евклидово расстояние между двумя точками.

Источник

Я думаю, что подход Али в целом - хороший путь, но есть общая проблема, называемая блокировкой карданного подвеса (или ТАКИЕ обсуждения по этой теме), когда используются углы Эйлера, т.е. Вы столкнетесь с этим, когда запишите более сложное движение, которое длится дольше, чем несколько тиков и, таким образом, приводит к большим угловым отклонениям в разных угловых направлениях.

Короче говоря, это означает, что у вас будет более одного математического представления для одной и той же позиции, в зависимости от порядка движений, которые вы сделали, чтобы туда добраться - и потери информации с другой стороны. Рассмотрим самолет, взлетающий в воздух слева направо. Ось X слева направо, ось Y направлена ​​вверх к воздуху. Следующие две последовательности движений приведут к одной и той же конечной позиции, хотя вы попадете туда совершенно разными путями:

Последовательность А:

  1. Вращение вокруг рыскания +90°
  2. Вращение вокруг шага +90°

Последовательность B:

  1. Вращение вокруг шага +90°
  2. Вращение вокруг крена +90°

В обоих случаях ваш самолет указывает на землю, и вы можете видеть его дно с вашей позиции.

Единственное решение этого состоит в том, чтобы избежать углов Эйлера и тем самым усложнить ситуацию. Кватернионы - лучший способ справиться с этим, но мне потребовалось некоторое время, чтобы понять это довольно абстрактное представление. Хорошо, этот ответ не продвигает вас дальше относительно вашей первоначальной проблемы, но может помочь вам избежать потери времени. Может быть, вы можете внести некоторые концептуальные изменения, чтобы настроить вашу идею.

Кей

Источник
Другие вопросы по тегам