Джулия: Оптимизируйте функцию стоимости с `Optim.jl` и`autodiff` для целых чисел

Question

Мне нравится оптимизировать (минимизировать) следующую функцию (quad_function) используя Optim.jl с автоматическим дифференцированием (autodiff=true).

Мои целевые функции раундов Real Значения для целых чисел и, следовательно, ступенчатый.

Как я использую autodiff вариант мой Real значения получают двойные числа (ForwardDiff.Dualс). Но к сожалению нет round функция реализована для ForwardDiff.Dual тип. Таким образом, я написал roundtoint64 функция, которая извлекает реальную часть. Такой подход вызывает проблемы при оптимизации.

using Plots
plotlyjs()

function roundtoint64(x)
  if typeof(x) <: ForwardDiff.Dual
    roundtoint64(x.value)
  else
    Int64(round(x))
  end
end

function quad_function(xs::Vector)
  roundtoint64(xs[1])^2 + roundtoint64(xs[2])^2
end

x, y = linspace(-5, 5, 100), linspace(-5, 5, 100)
z = Surface((x,y)->quad_function([x,y]), x, y)
surface(x,y,z, linealpha = 0.3)

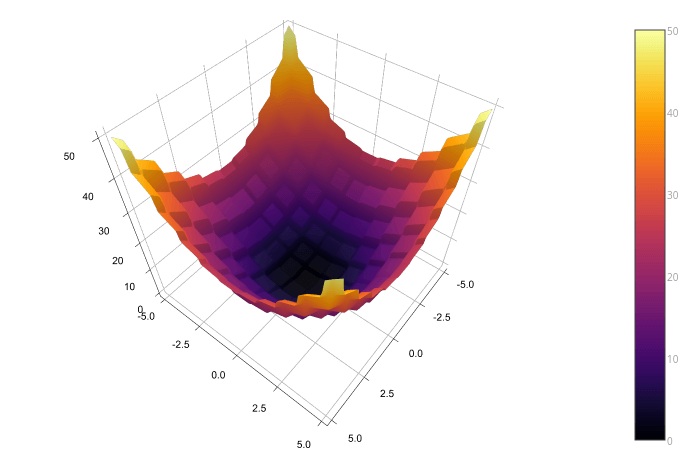
Вот так мой quad_function похоже: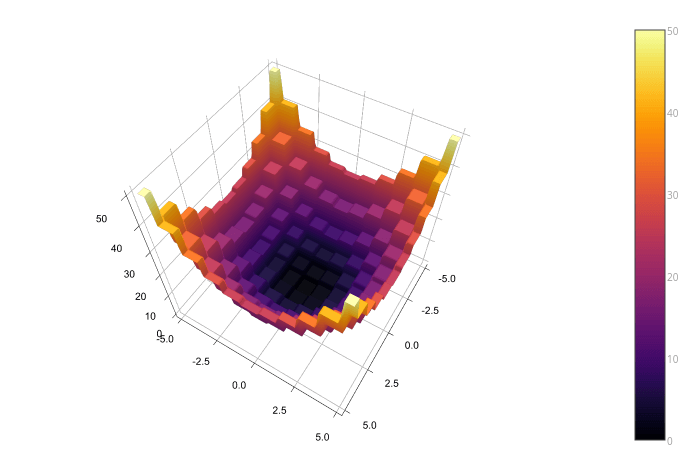

Проблема в том, что optimize функции сходятся сразу и не продолжаются.

using Optim

res = Optim.optimize(
  quad_function,
  [5.0,5.0],
  Newton(),
  OptimizationOptions(
    autodiff   = true,
    # show_trace = true
  ))

результат:

Results of Optimization Algorithm
 * Algorithm: Newton's Method
 * Starting Point: [5.0,5.0]
 * Minimizer: [5.0,5.0]
 * Minimum: 5.000000e+01
 * Iterations: 0
 * Convergence: true
   * |x - x'| < 1.0e-32: false
   * |f(x) - f(x')| / |f(x)| < 1.0e-32: false
   * |g(x)| < 1.0e-08: true
   * Reached Maximum Number of Iterations: false
 * Objective Function Calls: 1
 * Gradient Calls: 1


optimal_values  = Optim.minimizer(res) # [5.0, 5.0]
optimum         = Optim.minimum(res)   # 50.0

Я также попытался инициализировать optimize функция с вектором целых чисел [5,5] чтобы избежать округления, но это также вызывает проблемы с поиском начального размера шага в:

ERROR: InexactError()
 in alphainit(::Int64, ::Array{Int64,1}, ::Array{Int64,1}, ::Int64) at /home/sebastian/.julia/v0.5/Optim/src/linesearch/hz_linesearch.jl:63
 in optimize(::Optim.TwiceDifferentiableFunction, ::Array{Int64,1}, ::Optim.Newton, ::Optim.OptimizationOptions{Void}) at /home/sebastian/.julia/v0.5/Optim/src/newton.jl:69
 in optimize(::Function, ::Array{Int64,1}, ::Optim.Newton, ::Optim.OptimizationOptions{Void}) at /home/sebastian/.julia/v0.5/Optim/src/optimize.jl:169

Вопрос: есть ли способ сказать optimize исследовать только целое пространство?

Обновление: я думаю, что проблема с подходом к конвертации Int64 это то, что у меня больше нет ForwardDiff.Duals и, следовательно, не может вычислить какие-либо производные / градиенты. Как лучше round Как выглядит функция, которая округляет также вложенные двойные и возвращает двойные?

Answer 1

Я отвечу на ваше обновление более ориентированным на двойные числа ответом, так как Эрвин Кальвелаген опередил меня в исходном вопросе.

На самом деле, есть round функция реализована для ForwardDiff.Dual который имеет поведение, которое вы упомянули в своем первоначальном посте - он усекает компоненты частичной производной и применяется только round к реальной составляющей. Это в основном правильное определение, потому что производная от round равен нулю почти везде и не определен, где происходит шаг (т.е. с интервалами 0.5).

Это определение можно сделать "более правильным" путем распространения NaN s или ошибки в точках, где производная не определена, но с точки зрения практической AD, эта стратегия не слишком полезна. round Метод будет "выбирать сторону" в случае разрыва, поэтому для нас имеет смысл вручную выбирать "сторону" при получении производной. Это легко в случае round, поскольку производная по обе стороны разрыва равна нулю.

Вы можете использовать любое определение, которое хотите, переписав определенный в настоящее время метод, но, как вы указали, round промежуточные частные производные могут привести к неправильной общей производной. По сути это связано с тем, что вы больше не дифференцируете одну и ту же целевую функцию.

Answer 2

Как отметил Эрвин Кальвелаген в комментариях к моему вопросу: с данным алгоритмом и решателем нет решения этой проблемы.

Таким образом, я немного изменил свою функцию стоимости, чтобы иметь хотя бы несколько градиентов, но это все еще не гладко:

function quad_function_with_gradient(xs::Vector)
  round(xs[1])*xs[1] + round(xs)[2]*xs[2]
end

который выглядит так:

Но тогда мне все же пришлось решить проблему округления двойных чисел. Поэтому я написал round функция, которая всегда округляет вещественную часть и частичные:

using Optim

roundpartials{T<:ForwardDiff.Partials}(partials::T) = (round(v) for v in partials.values)

Base.round{T<:ForwardDiff.Dual}(dual::T) = ForwardDiff.Dual(
  round(dual.value),
  roundpartials(dual.partials)...)

Это дает мне решение, но немного другой проблемы:

res = Optim.optimize(
  quad_function,
  [5.0,5.0],
  Newton(),
  OptimizationOptions(
    autodiff   = true
  ))

Results of Optimization Algorithm
 * Algorithm: Newton's Method
 * Starting Point: [5.0,5.0]
 * Minimizer: [0.0,0.0]
 * Minimum: 0.000000e+00
 * Iterations: 1
 * Convergence: true
   * |x - x'| < 1.0e-32: false
   * |f(x) - f(x')| / |f(x)| < 1.0e-32: false
   * |g(x)| < 1.0e-08: true
   * Reached Maximum Number of Iterations: false
 * Objective Function Calls: 5
 * Gradient Calls: 5

Ребята, решать вам, будет ли это возможным решением.